Coordenadas polares para niños
Las coordenadas polares son una forma especial de ubicar puntos en un plano, como si fuera un mapa. Imagina que tienes un punto central y una línea recta que sale de él. Para encontrar cualquier otro punto, solo necesitas dos cosas:
- La distancia desde el punto central hasta el punto que buscas.
- El ángulo que se forma entre la línea recta de referencia y la línea que une el punto central con el punto que buscas.
Este sistema es muy útil en física y trigonometría para describir movimientos circulares o cosas que giran.
Para entenderlo mejor, piensa en un sistema de referencia:
- Un punto central llamado origen o polo (como el centro de un reloj).
- Una línea recta que sale del origen, llamada eje polar (como la manecilla de las 3 en un reloj).
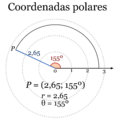
Con esto, cualquier punto P se describe con un par de números (r, θ):
- r es la distancia desde el origen hasta P. Se le llama «coordenada radial» o «radio vector». Siempre es un número positivo o cero.
- θ (la letra griega "theta") es el ángulo que se forma. Se le llama «coordenada angular» o «ángulo polar». Este ángulo se mide girando en sentido contrario a las agujas del reloj desde el eje polar.
Si el punto es el origen, r es 0, y el ángulo puede ser cualquiera, ya que no hay una dirección específica.
Contenido
Historia de las Coordenadas Polares
Aunque la idea de usar ángulos y distancias para ubicar cosas existe desde hace mucho tiempo, el sistema de coordenadas polares como lo conocemos hoy se desarrolló en el siglo XVII.
- Los antiguos astrónomos como Hiparco de Nicea (hace más de 2000 años) ya usaban tablas con ángulos y distancias para estudiar las estrellas y la navegación.
- Arquímedes, un gran matemático griego, describió una curva llamada la espiral de Arquímedes, donde el radio depende del ángulo. Esto fue un paso importante.
En tiempos más recientes:
- En el siglo XVII, matemáticos como Grégoire de Saint-Vincent y Bonaventura Cavalieri empezaron a usar ideas similares a las coordenadas polares para resolver problemas de geometría.
- Isaac Newton, famoso por la ley de la gravedad, también incluyó un sistema parecido a las coordenadas polares en uno de sus libros en 1671.
- Jacob Bernoulli usó en 1691 un sistema con un "polo" y un "eje polar", que son los nombres que usamos hoy.
- El término "coordenadas polares" fue usado por primera vez por Gregorio Fontana en el siglo XVIII.
Cómo se representan los puntos en Coordenadas Polares
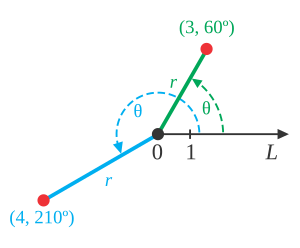
Para entender cómo se ubican los puntos:
- El punto (3, 60°) significa que está a 3 unidades de distancia del origen y a un ángulo de 60° desde el eje polar.
- El punto (4, 210°) significa que está a 4 unidades de distancia del origen y a un ángulo de 210° desde el eje polar.
Una curiosidad de las coordenadas polares es que un mismo punto puede tener muchas representaciones diferentes. Por ejemplo, el punto (3, 60°) es el mismo que (3, 420°) (porque 420° es 60° + 360°, una vuelta completa). También puede ser el mismo que (-3, 240°), aunque esto es menos común.
Para evitar confusiones, normalmente se elige que la distancia r sea siempre positiva (o cero) y que el ángulo θ esté en un rango específico, como entre 0° y 360° (o entre -180° y 180°).
Los ángulos en coordenadas polares se pueden medir en grados o en radianes. Los grados son comunes en navegación, mientras que los radianes se usan más en matemáticas y física.
Cómo convertir Coordenadas
A veces, necesitamos cambiar de coordenadas polares a coordenadas rectangulares (las que usas en un plano cartesiano con ejes X e Y) o viceversa.
De Coordenadas Polares a Rectangulares
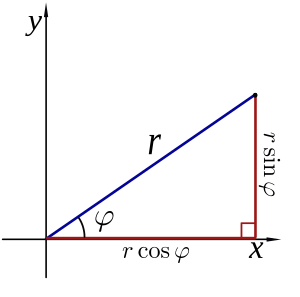
Si tienes un punto en coordenadas polares (r, θ), puedes encontrar sus coordenadas rectangulares (x, y) usando estas fórmulas:
- x = r × cos(θ)
- y = r × sen(θ)
Aquí, "cos" es el coseno y "sen" es el seno, que son funciones trigonométricas.
De Coordenadas Rectangulares a Polares
Si tienes un punto en coordenadas rectangulares (x, y), puedes encontrar su distancia r y su ángulo θ:
- La distancia r se calcula con el Teorema de Pitágoras: r = √(x² + y²)
- Para el ángulo θ, la cosa es un poco más complicada porque depende de en qué parte del plano esté el punto. Se usa la función tangente inversa (arctan o atan2) para encontrar el ángulo correcto.
Ecuaciones Polares
Una ecuación polar es una fórmula que describe una curva usando coordenadas polares. Muchas curvas que son difíciles de describir con coordenadas rectangulares, son muy sencillas con coordenadas polares.
Algunas curvas famosas que se describen fácilmente con ecuaciones polares son:
Circunferencia
Una circunferencia con centro en el origen y radio a tiene una ecuación muy simple en coordenadas polares:
- r(θ) = a
Esto significa que, no importa el ángulo, la distancia al centro siempre es la misma (el radio).
Línea Recta
Las líneas que pasan por el origen (el polo) se describen con un ángulo fijo:
- θ = φ (donde φ es el ángulo de la línea)
Rosa Polar
La rosa polar es una curva que parece una flor con pétalos. Su ecuación es:
- r(θ) = a × cos(kθ)
Donde k es un número entero. Si k es impar, la rosa tiene k pétalos. Si k es par, tiene 2k pétalos. La letra a controla el tamaño de los pétalos.
Espiral de Arquímedes
La espiral de Arquímedes es una espiral famosa donde la distancia al centro aumenta de forma constante a medida que el ángulo gira. Su ecuación es:
- r(θ) = a + bθ
Donde a y b son números que controlan cómo se ve la espiral.
Secciones Cónicas
Las secciones cónicas (como elipses, parábolas e hipérbolas) también tienen ecuaciones sencillas en coordenadas polares si uno de sus puntos especiales (llamados focos) está en el origen.
- r = ℓ / (1 + e × cos θ)
Aquí, e es la excentricidad (que dice qué tan "estirada" es la forma) y ℓ es una medida de la curva.
Números Complejos
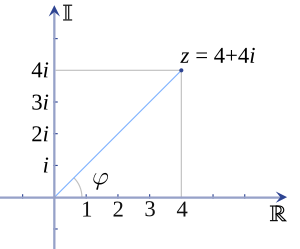
Los números complejos se pueden ver como puntos en un plano. Se pueden representar con coordenadas rectangulares (x + iy) o con coordenadas polares (r × (cosθ + i senθ)). La forma polar es muy útil para multiplicar, dividir o elevar a una potencia números complejos, ya que las operaciones se vuelven mucho más sencillas.
Cálculo Matemático
El cálculo infinitesimal (que estudia cómo cambian las cosas) también se puede aplicar a las ecuaciones en coordenadas polares. Esto permite calcular cosas como la pendiente de una curva o el área de una región.
Cálculo de Áreas
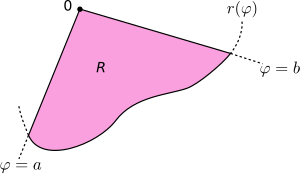
Para calcular el área de una región delimitada por una curva polar, se usa una fórmula especial que involucra una integral:
- Área = ½ ∫ r(θ)² dθ
Esta fórmula se obtiene dividiendo la región en muchos pequeños sectores circulares y sumando sus áreas.
Coordenadas en más Dimensiones
Las coordenadas polares son para dos dimensiones (un plano). Pero se pueden extender a tres dimensiones de dos maneras:
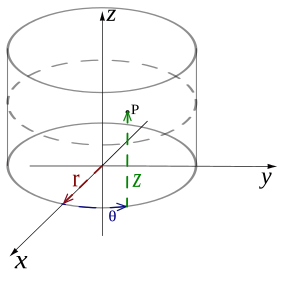
Coordenadas Cilíndricas
Las coordenadas cilíndricas añaden una tercera coordenada, h, que mide la altura de un punto sobre el plano. Así, un punto se describe como (r, θ, h). Es como las coordenadas polares, pero con una altura extra, como si fuera un cilindro.
Coordenadas Esféricas
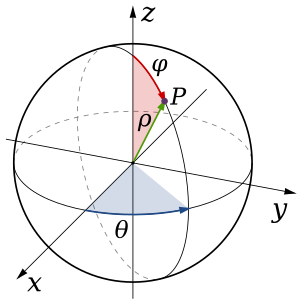
Las coordenadas esféricas usan tres coordenadas angulares y de distancia: (ρ, φ, θ).
- ρ (letra griega "rho") es la distancia al origen.
- φ (letra griega "phi") es el ángulo desde el eje Z (como la latitud en la Tierra).
- θ es el ángulo alrededor del eje Z (como la longitud en la Tierra).
Este sistema es muy útil para describir puntos en una esfera, como la posición de un avión o un barco en la Tierra.
Aplicaciones de las Coordenadas Polares
Las coordenadas polares son muy útiles cuando lo que estudiamos tiene que ver con un punto central o con giros.
- En la navegación, tanto en barcos como en aviones, se usan coordenadas polares para indicar la dirección y la distancia a un destino.
Modelado de Sistemas
- Son ideales para describir sistemas que tienen una simetría radial, es decir, que se ven igual en todas las direcciones desde un punto central. Por ejemplo, el flujo de agua alrededor de un pozo o los campos gravitatorios alrededor de un planeta.
- También se usan para describir cómo funcionan los micrófonos, mostrando qué tan sensibles son a los sonidos que vienen de diferentes direcciones.
Cálculo de Límites
- En matemáticas avanzadas, las coordenadas polares ayudan a resolver problemas de límites en funciones, especialmente cuando se acercan a un punto problemático como el origen.
Galería de imágenes
Véase también
 En inglés: Polar coordinate system Facts for Kids
En inglés: Polar coordinate system Facts for Kids


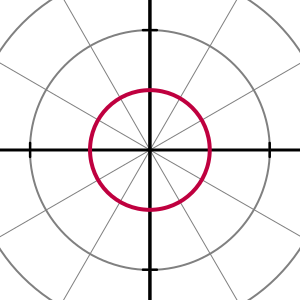
 (θ) = 1
(θ) = 1