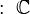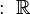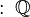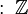Número imaginario para niños
En matemáticas, un número imaginario es un tipo especial de número complejo que tiene una parte real igual a cero. Imagina que es un número que se forma al multiplicar un número real por la unidad imaginaria, que se representa con la letra i.
Por ejemplo, `3i` es un número imaginario. También lo son `i` o `-i`. En general, un número imaginario se escribe como `bi`, donde `b` es un número real cualquiera.
Al principio, en el siglo XVII, el filósofo y matemático René Descartes usó la palabra "imaginario" para referirse a estos números de forma un poco despectiva, como si no fueran "reales" o útiles. Sin embargo, con el tiempo, matemáticos importantes como Leonhard Euler (en el siglo XVIII) y Augustin-Louis Cauchy y Carl Friedrich Gauss (a principios del siglo XIX) demostraron su gran utilidad, y el concepto fue ampliamente aceptado.
Un número imaginario `bi` se puede sumar a un número real `a` para formar un número complejo de la forma `a + bi`. Aquí, `a` es la parte real del número complejo, y `bi` es la parte imaginaria.
Contenido
¿Qué son los Números Imaginarios?
Los números imaginarios se basan en la unidad imaginaria `i`. Esta unidad es un número muy especial que, al elevarse al cuadrado, da como resultado -1. Es decir: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i^{2}= -1
Esto es sorprendente porque, en los números reales, cualquier número elevado al cuadrado (multiplicado por sí mismo) siempre da un resultado positivo o cero. Los números imaginarios nos permiten trabajar con la raíz cuadrada de números negativos, algo que no es posible solo con los números reales.
La Unidad Imaginaria 'i'
La unidad imaginaria `i` es la base de todos los números imaginarios. Su propiedad principal es que `i` al cuadrado es igual a -1. Esto abre un mundo nuevo en las matemáticas, permitiendo resolver ecuaciones que antes no tenían solución en el conjunto de los números reales.
Historia de los Números Imaginarios
Aunque parezcan extraños, los números imaginarios tienen una historia fascinante.
Primeros Pasos y Desafíos
Se cree que el matemático e ingeniero griego Herón de Alejandría fue el primero en encontrarse con un cálculo que implicaba la raíz cuadrada de un número negativo. Sin embargo, fue Rafael Bombelli, un matemático italiano del siglo XVI, quien en 1572 estableció las primeras reglas para trabajar con estos números. Otros matemáticos, como Gerolamo Cardano, también los mencionaron.
En esa época, los números imaginarios (y también los números negativos) no se entendían bien. Algunos los veían como algo ficticio o inútil, de forma similar a cómo se veía el número cero en sus inicios.
La Aceptación y Nombres Famosos
Muchos matemáticos tardaron en aceptar los números imaginarios. Entre ellos, René Descartes, quien en su libro La Géométrie usó el término "imaginario" con la intención de restarle importancia.
El uso de los números imaginarios no fue ampliamente aceptado hasta los trabajos de Leonhard Euler (quien vivió de 1707 a 1783) y Carl Friedrich Gauss (de 1777 a 1855). Ellos demostraron lo útiles que eran. Además, Caspar Wessel (1745-1818) fue el primero en describir cómo los números complejos (que incluyen a los imaginarios) podían representarse como puntos en un plano, dándoles un significado geométrico.
Fue en 1777 cuando Leonhard Euler le dio a la raíz cuadrada de -1 el nombre de i, por "imaginario". Incluso Gottfried Leibniz, en el siglo XVII, se refirió a la raíz cuadrada de -1 como "ese anfibio entre el ser y el no ser", mostrando lo difícil que era para los matemáticos de la época entender su naturaleza.
En campos como la ingeniería eléctrica, a veces se usa la letra j en lugar de i para la unidad imaginaria. Esto es para evitar confusiones, ya que la letra `i` se usa tradicionalmente para representar la corriente eléctrica.
Momentos Clave en la Historia
| Año | Acontecimiento |
|---|---|
| 1572 | Rafael Bombelli realiza cálculos utilizando números imaginarios. |
| 1777 | Leonhard Euler utiliza el símbolo “i” para representar la raíz cuadrada de -1. |
| 1811 | Jean-Robert Argand crea la representación gráfica del Plano complejo también conocida como plano de Argand. |
Formas de Representar los Números Imaginarios
Además de la forma `bi`, los números imaginarios se pueden representar de otras maneras:
- Como un par ordenado de números reales: `z = (0, y)`. Aquí, el primer número es la parte real (que es cero) y el segundo es la parte imaginaria.
- De forma trigonométrica: `z = r(cos(π/2) + i sin(π/2))`, donde `r` es un número real. Esta expresión también se puede escribir como `z = re^(iπ/2)`.
- En algunas áreas, como la ingeniería eléctrica, la unidad imaginaria se representa con `j` en lugar de `i` para evitar confusiones con la corriente eléctrica.
Propiedades de los Números Imaginarios
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
(mod representa el residuo) |
|
Todo número imaginario se puede escribir como `ib`, donde `b` es un número real e `i` es la unidad imaginaria.
Si elevamos un número imaginario al cuadrado, obtenemos un número real negativo. Por ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (bi)^2 = b^2 i^2 = b^2 (-1)= -b^2
Esto significa que la raíz cuadrada de un número real negativo siempre será un número imaginario. Por ejemplo, la raíz cuadrada de `-b` (donde `b` es un número positivo) es `i√b`.
Cada número complejo se puede escribir de una única manera como la suma de un número real y un número imaginario: 
Aquí, `a` es la parte real y `bi` es la parte imaginaria.
Los números imaginarios, junto con los números reales, forman un conjunto más grande llamado números complejos. Este conjunto, representado por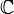 
, extiende el conjunto de los números reales 
.
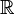Es importante saber que los números imaginarios no se pueden "ordenar" como los números reales. Por ejemplo, con los números reales, podemos decir que `1 > 0` o `-1 < 0`. Pero con los números imaginarios, no podemos decir si `i` es mayor o menor que `0`. Si intentáramos hacerlo, llegaríamos a contradicciones matemáticas.
Aplicaciones de los Números Imaginarios
Aunque su nombre sugiera lo contrario, los números imaginarios son muy reales y útiles en muchas áreas de la ciencia y la ingeniería:
- Permiten encontrar las raíces cuadradas de números negativos, lo cual es fundamental para resolver muchas ecuaciones.
- En la física cuántica, la unidad imaginaria simplifica la forma de describir cómo cambian los estados cuánticos con el tiempo.
- En la teoría de circuitos y la corriente alterna, los números imaginarios se usan para representar magnitudes como los fasores. Esto hace que los cálculos en estos campos sean mucho más sencillos.
Véase también
En inglés: Imaginary number Facts for Kids
Wikcionario tiene definiciones y otra información sobre número imaginario.
|
- Menos uno
- Octonión
