Fasor para niños
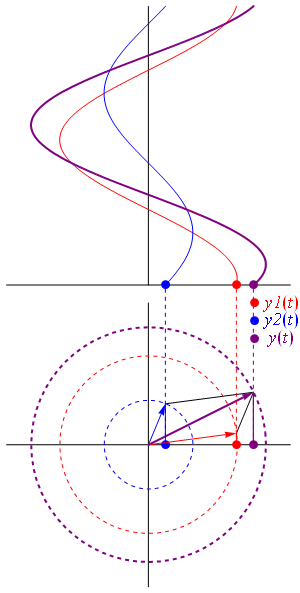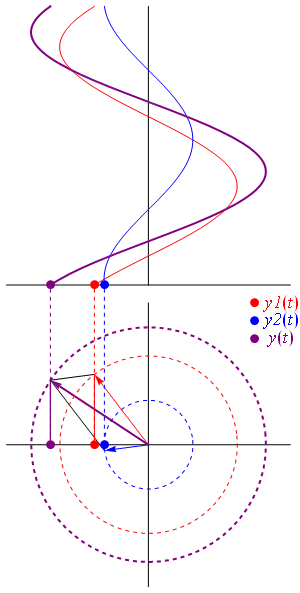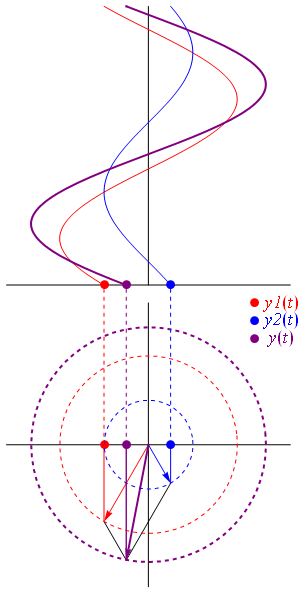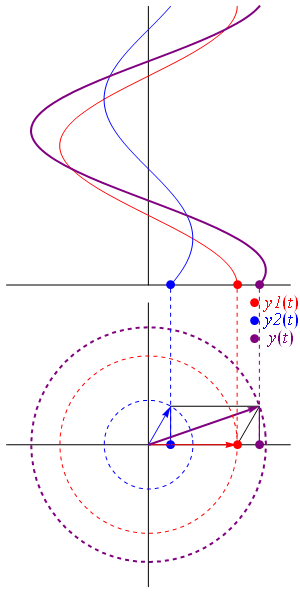
Un fasor es una herramienta gráfica que nos ayuda a entender y representar números complejos que describen ondas o vibraciones. Imagina que es como una flecha que gira. Esta flecha nos muestra qué tan grande es una onda (su amplitud) y en qué punto de su ciclo se encuentra (su fase).
Los fasores son muy útiles en campos como la ingeniería eléctrica, la óptica (estudio de la luz), la ingeniería de telecomunicaciones y la acústica (estudio del sonido). La longitud de la flecha del fasor nos dice la amplitud de la onda, y el ángulo que forma con un eje de referencia nos indica su fase.
Una de las principales ventajas de los fasores es que nos permiten sumar varias ondas de la misma frecuencia de una manera sencilla. Si tienes varias ondas que se encuentran en un mismo punto, puedes dibujar un fasor para cada una y luego sumarlos como si fueran flechas. El fasor resultante te mostrará la amplitud y la fase de la nueva onda que se forma al combinarse todas.
Contenido
¿Qué es una onda sinusoidal?
Para entender los fasores, primero necesitamos saber qué es una onda sinusoidal. Es un tipo de onda que se repite de forma suave y regular, como las ondas que se forman en el agua cuando tiras una piedra. Se describe con una fórmula matemática:
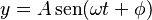
Aquí, cada letra tiene un significado:
- y: Es el valor de la onda en un momento dado.
- A: Es la amplitud, que nos dice qué tan alta o intensa es la onda. Es su valor máximo.
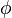: Es la fase, un número que nos indica el punto de inicio de la onda en su ciclo. Se mide en radianes.- ω: Es la frecuencia angular, que nos dice qué tan rápido cambia la onda. Está relacionada con la frecuencia normal (f) por la fórmula
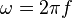. - t: Es el tiempo.
¿Cómo se representa un fasor?
Un fasor es una forma de "guardar" la información de la amplitud (A) y la fase (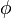
) de una onda sinusoidal en un solo número complejo. Se escribe así:
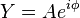
O, de una forma más sencilla y común en ingeniería, usando la notación angular:
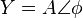
En esta notación, 'A' es la amplitud y '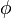' es el ángulo de fase. En ingeniería eléctrica, este ángulo a menudo se expresa en grados en lugar de radianes.
¿Para qué se usan los fasores?
Los fasores son muy útiles para simplificar el análisis de circuitos eléctricos de corriente alterna (AC). En estos circuitos, las tensiones y corrientes cambian constantemente como ondas. Usando fasores, podemos tratar estas ondas como si fueran números fijos, lo que hace los cálculos mucho más fáciles.
Leyes de circuitos con fasores
Las leyes básicas de los circuitos, como la Ley de Ohm y las Leyes de Kirchhoff, que usas para circuitos de corriente continua, también se pueden aplicar a circuitos de corriente alterna usando fasores.
- Ley de Ohm para resistores: En un resistor, la relación entre voltaje (V), corriente (I) y resistencia (R) sigue siendo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V = I \cdot R , pero usando los fasores de V e I.
- Ley de Ohm para otros componentes: Para componentes como bobinas (inductores) y condensadores (capacitores), la relación es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V = Z \cdot I , donde 'Z' es la impedancia. La impedancia es como una resistencia, pero para corriente alterna, y también se representa con un fasor.
- Leyes de Kirchhoff: Las leyes que nos dicen cómo se suman las corrientes y los voltajes en un circuito también funcionan perfectamente con fasores.
Suma de ondas
Cuando varias ondas de la misma frecuencia se combinan, el resultado es otra onda de la misma frecuencia. Los fasores nos permiten sumar estas ondas de forma gráfica, como si estuviéramos sumando flechas. La longitud de la flecha resultante nos da la amplitud de la nueva onda, y su ángulo nos da su fase. Esto es muy útil para saber la intensidad final de la onda combinada.
Transformada fasorial
La transformada fasorial es un proceso que nos permite convertir una onda sinusoidal que cambia con el tiempo en su representación fasorial (un número complejo). Esto nos ayuda a pasar del "dominio del tiempo" (donde vemos cómo la onda cambia segundo a segundo) al "dominio de la frecuencia" (donde la onda se representa como un fasor fijo).
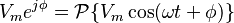
La notación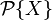 
significa "la transformada fasorial de X". También existe la transformada fasorial inversa, que nos permite hacer el camino de vuelta, del fasor a la onda que cambia con el tiempo.
Operaciones con fasores
Los fasores, al ser números complejos, se pueden sumar, restar, multiplicar y dividir.
- Para sumar y restar fasores, es más fácil usar su forma cartesiana (como un punto en un plano, por ejemplo, 3 + 4i).
- Para multiplicar y dividir fasores, es más sencillo usar su forma polar (la que tiene la amplitud y el ángulo, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A \angle \phi ).
Galería de imágenes
-
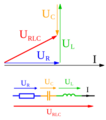
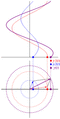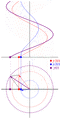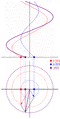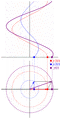
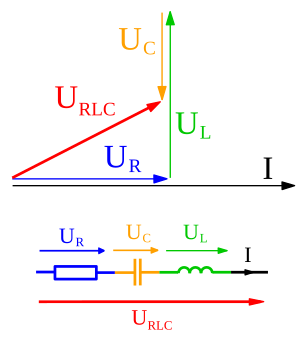
Diagrama fasorial de la impedancia de distintos elementos de un circuito. El fasor rojo es la impedancia total en serie, suma de los otros tres fasores.
-
Evolución de dos magnitudes senoidales de la misma frecuencia y de su suma en forma temporal y fasorial.
Véase también
En inglés: Phasor Facts for Kids
