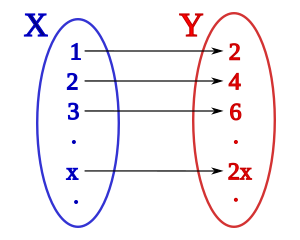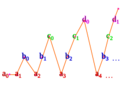Conjunto numerable para niños
Un conjunto numerable en matemáticas es una colección de elementos que puedes "contar", ya sea porque tiene un número limitado de elementos (es decir, es un conjunto finito) o porque puedes emparejar cada uno de sus elementos con los números naturales (0, 1, 2, 3, ...).
Imagina que tienes una lista de cosas. Si puedes darle un número a cada cosa de la lista sin que te falten números o te sobren cosas, entonces esa lista es un conjunto numerable.
En 1874, un matemático llamado Georg Cantor fue quien propuso la idea de los conjuntos numerables. Él los comparó con otros conjuntos que son tan grandes que no se pueden contar de esta manera, a los que llamó conjuntos no numerables. Hoy en día, los conjuntos numerables son muy importantes en una parte de las matemáticas llamada matemática discreta.
Contenido
¿Qué es un conjunto numerable?
Un conjunto se considera numerable si puedes establecer una "correspondencia uno a uno" entre sus elementos y los números naturales. Esto significa que a cada elemento del conjunto le asignas un número natural único, y a cada número natural le corresponde un elemento único del conjunto.
Por ejemplo, si tienes el conjunto de los números pares {0, 2, 4, 6, ...}, puedes hacer esta correspondencia:
- 0 se empareja con 0
- 2 se empareja con 1
- 4 se empareja con 2
- 6 se empareja con 3
Y así sucesivamente. Aunque el conjunto de los números pares es infinito, podemos "contarlos" porque podemos emparejarlos con los números naturales.
Si un conjunto es infinito y se puede emparejar uno a uno con los números naturales, se le llama infinito numerable.
Historia de los conjuntos numerables
La idea de los conjuntos numerables fue presentada por Georg Cantor en 1874. En su primer trabajo sobre la teoría de conjuntos, Cantor demostró algo muy sorprendente: el conjunto de los números reales (que incluye números con decimales infinitos y no repetitivos, como pi) es tan grande que no se puede contar. Esto significa que no todos los conjuntos infinitos son numerables.
Cantor usó estas correspondencias uno a uno para comparar el "tamaño" de diferentes conjuntos, incluso los infinitos. Su trabajo fue muy importante porque cambió la forma en que los matemáticos entendían el infinito.
¿Por qué es importante la numerabilidad?
Antes de Cantor, muchos matemáticos pensaban que el infinito era solo una idea de algo que nunca termina. Pero Cantor demostró que hay diferentes "tipos" de infinito. Al comparar conjuntos, pudo mostrar que algunos infinitos son "más grandes" que otros.
Por ejemplo, el conjunto de los números algebraicos (números que son solución de ecuaciones con números enteros) es numerable. Pero el conjunto de todos los números reales no lo es. Esto significa que hay muchos más números reales que números algebraicos, ¡incluso si ambos conjuntos son infinitos!
Ejemplos de conjuntos numerables
Un conjunto es numerable si es finito o si tiene el mismo "tamaño" (o cardinalidad, que es el término técnico) que el conjunto de los números naturales. Si no es así, se dice que es incontable.
Aquí tienes algunos ejemplos de conjuntos numerables:
- Números naturales: {0, 1, 2, 3, ...} Por definición, este es el conjunto base para la numerabilidad.
- Números enteros: {..., -2, -1, 0, 1, 2, ...} Aunque parece que hay el doble de números que los naturales (positivos y negativos), podemos emparejarlos uno a uno:
* 0 se empareja con 0 * 1 se empareja con 1 * -1 se empareja con 2 * 2 se empareja con 3 * -2 se empareja con 4 Y así sucesivamente.
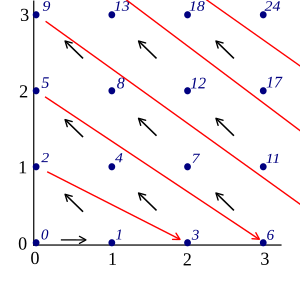
- Números racionales: Son las fracciones, como 1/2, -3/4, 5/1. Parece que hay muchísimos, pero Cantor demostró que también son numerables. Puedes imaginarlos organizados en una tabla y contarlos siguiendo un patrón en zigzag.
- Cualquier subconjunto de un conjunto numerable: Si tienes un conjunto numerable, cualquier parte de él (subconjunto) también será numerable. Por ejemplo, el conjunto de los números primos {2, 3, 5, 7, ...} es un subconjunto de los números naturales, y también es numerable.
- Uniones de conjuntos numerables: Si tienes varias colecciones de elementos, y cada una de esas colecciones es numerable, entonces si las juntas todas, el nuevo conjunto también será numerable.
¿Qué conjuntos no son numerables?
El ejemplo más famoso de un conjunto no numerable es el de los números reales. Estos son todos los números que puedes encontrar en una línea numérica, incluyendo los decimales infinitos no repetitivos. Georg Cantor demostró que no importa cómo intentes emparejarlos con los números naturales, siempre te quedarán números reales sin emparejar. Esto significa que el conjunto de los números reales es "más grande" que el conjunto de los números naturales.
Galería de imágenes
-
Ejercicio esquemático para comprobar que los números racionales son contables.
-
Enumeración de un número contable de conjuntos numerables.
Véase también
En inglés: Countable set Facts for Kids
