Lógica filosófica para niños

La lógica filosófica es una parte de la filosofía que se encarga de usar herramientas de la lógica para resolver preguntas filosóficas. A menudo, esto se hace creando nuevos sistemas lógicos, como la lógica modal, que nos ayudan a entender mejor conceptos como la posibilidad o la necesidad.

Algunas personas ven la lógica filosófica de una manera más amplia. Para ellos, es el estudio de qué es la lógica en general y hasta dónde llega. En este sentido, sería lo mismo que la filosofía de la lógica, que también explora qué significa la lógica y sus ideas principales. En este artículo, nos centraremos en la lógica filosófica en su sentido más específico, como un área de investigación dentro de la filosofía de la lógica.

Un tema importante en la lógica filosófica es cómo organizar los muchos sistemas lógicos no clásicos que existen, muchos de los cuales son bastante nuevos. Una forma común de clasificarlos es dividirlos en lógicas extendidas y lógicas desviadas. La lógica en sí misma se puede definir como el estudio de las inferencias válidas. La lógica clásica es la forma más común de lógica. Establece reglas de inferencia que coinciden con lo que muchas personas consideran lógico, como el principio del tercero excluido (algo es verdadero o falso, no hay una tercera opción), la eliminación de la doble negación (si algo no es no verdadero, entonces es verdadero) y la bivalencia de la verdad (una afirmación es solo verdadera o falsa).

Las lógicas extendidas son sistemas que se basan en la lógica clásica y sus reglas. Pero añaden nuevos símbolos y reglas para explorar nuevos temas. Por ejemplo, la lógica modal alética usa nuevos símbolos para hablar no solo de lo que es verdadero, sino también de lo que es posible o necesariamente verdadero. A menudo se usa con la idea de los mundos posibles: algo es posible si es verdad en algún mundo posible, y es necesario si es verdad en todos los mundos posibles. La lógica deóntica se relaciona con la ética y nos ayuda a entender formalmente ideas como la obligación y el permiso. La lógica temporal organiza las relaciones de tiempo entre afirmaciones, como si algo es verdad en algún momento o siempre, o si es verdad en el futuro o en el pasado. La lógica epistémica se usa en la epistemología (el estudio del conocimiento). Puede expresar no solo lo que es, sino también lo que alguien cree o sabe que es. Sus reglas nos dicen qué se puede deducir de lo que alguien sabe o cree. Las lógicas de orden superior no aplican la lógica clásica a nuevos campos, sino que la hacen más general al permitir hablar no solo de objetos individuales, sino también de propiedades.

Las lógicas desviadas, a diferencia de las extendidas, no aceptan algunos principios básicos de la lógica clásica y a menudo se consideran sus rivales. La lógica intuicionista cree que algo es verdadero solo si se puede probar. Por eso, no acepta algunas reglas de la lógica clásica que no encajan con esta idea. La lógica libre cambia la lógica clásica para evitar problemas con nombres que no se refieren a nada real, como "Papá Noel". Las lógicas plurivalentes permiten más de dos valores de verdad (verdadero y falso), rechazando así la bivalencia. Las lógicas paraconsistentes pueden manejar contradicciones sin que todo el sistema se vuelva absurdo. Lo hacen evitando el "principio de explosión" de la lógica clásica. La lógica relevante es un tipo importante de lógica paraconsistente. No solo evita la explosión, sino que también exige que, para que una afirmación "si... entonces..." sea verdadera, las dos partes deben estar relacionadas.

¿Qué es la lógica filosófica?

El término "lógica filosófica" se usa de diferentes maneras. En su sentido más específico, que es el que tratamos aquí, la lógica filosófica es la parte de la filosofía que usa métodos lógicos para resolver problemas filosóficos. Esto a menudo implica crear nuevos sistemas lógicos. Estos sistemas pueden extender la lógica clásica a nuevas áreas o modificarla para incluir ideas lógicas que la lógica clásica no aborda bien.

Así, la lógica filosófica estudia diferentes tipos de lógicas no clásicas, como la lógica modal y la lógica deóntica. De esta manera, conceptos filosóficos importantes como la posibilidad, la necesidad, la obligación, el permiso y el tiempo se tratan de forma lógica y precisa. Se busca entender cómo se relacionan entre sí en términos de inferencias.

Algunos pensadores entienden la lógica filosófica de una forma más amplia. Para ellos, es el estudio de qué es la lógica en general y cuál es su alcance. Desde este punto de vista, investiga varios problemas filosóficos que surgen de la lógica, incluyendo sus conceptos fundamentales. En este sentido más amplio, puede ser lo mismo que la filosofía de la lógica, donde se discuten estos temas. En este artículo, nos enfocamos solo en la idea más específica de la lógica filosófica. En este sentido, es un área dentro de la filosofía de la lógica.

Un aspecto clave de la lógica filosófica es entender qué es la lógica y qué papel juegan las lógicas filosóficas en ella. La lógica se puede definir como el estudio de las inferencias válidas. Una inferencia es el paso en el razonamiento donde pasamos de unas ideas iniciales (premisas) a una conclusión. A menudo, también se usa la palabra "argumento". Una inferencia es válida si es imposible que las premisas sean verdaderas y la conclusión sea falsa. Esto significa que si las premisas son verdaderas, la conclusión también debe serlo. Esto se puede explicar con reglas de inferencia: una inferencia es válida si su estructura sigue una regla de inferencia.

Los diferentes sistemas lógicos tienen distintas formas de decidir cuándo una inferencia es válida. Esto significa que usan diferentes reglas de inferencia. La forma más común de entender la validez se llama lógica clásica. Pero la lógica filosófica se ocupa de la lógica no clásica: estudia sistemas de inferencia alternativos. Hay dos razones principales para hacer esto. Para algunos, la lógica clásica es demasiado limitada: no cubre muchos temas filosóficos interesantes. Esto se puede solucionar extendiendo la lógica clásica con símbolos adicionales para tratar otras áreas de forma lógica. Otros ven fallos en la propia lógica clásica e intentan ofrecer una forma diferente de entender la inferencia. Esto suele llevar al desarrollo de lógicas desviadas, que cambian los principios fundamentales de la lógica clásica para corregir sus supuestos defectos.

Cómo se clasifican las lógicas

Los avances recientes en lógica han llevado a la aparición de muchos sistemas lógicos diferentes. Esto contrasta mucho con el dominio histórico de la lógica aristotélica, que fue considerada la única lógica válida durante más de dos mil años. Los libros modernos sobre lógica a menudo presentan estos sistemas como una lista de temas separados, sin una clasificación clara. Sin embargo, una clasificación que se menciona a menudo en la literatura académica, propuesta por Susan Haack, distingue entre lógica clásica, lógicas extendidas y lógicas desviadas.

Esta clasificación se basa en la idea de que la lógica clásica (es decir, la lógica proposicional y la lógica de primer orden) formaliza algunas de las ideas lógicas más comunes. En este sentido, es una base para entender las reglas que rigen las inferencias válidas.

• Lógicas extendidas: Aceptan esta base y la amplían a nuevas áreas. Esto suele hacerse añadiendo nuevo vocabulario, por ejemplo, para expresar necesidad, obligación o tiempo. Estos nuevos símbolos se integran en el sistema lógico especificando qué nuevas reglas de inferencia se aplican a ellos. Por ejemplo, la posibilidad se deduce de la necesidad.
• Lógicas desviadas: Por otro lado, rechazan algunos de los principios básicos de la lógica clásica. En este sentido, no son solo extensiones, sino que a menudo se presentan como sistemas rivales que ofrecen una forma diferente de entender las leyes de la lógica.

En un lenguaje más técnico, la diferencia entre lógicas extendidas y desviadas a veces se explica de otra manera. Desde este punto de vista, una lógica es una extensión de la lógica clásica si cumple dos condiciones: (1) Todas las fórmulas bien formadas de la lógica clásica también son fórmulas bien formadas en ella. (2) Todas las inferencias válidas en la lógica clásica también son inferencias válidas en ella.

Para una lógica desviada, en cambio: (a) Su conjunto de fórmulas bien formadas es el mismo que el de la lógica clásica. (b) Algunas inferencias válidas en la lógica clásica no son válidas en ella.

El término "lógica cuasi-desviada" se usa si: (i) Introduce vocabulario nuevo, pero todas las fórmulas bien formadas de la lógica clásica también son fórmulas bien formadas en ella. (ii) Incluso cuando se limita a inferencias que usan solo el vocabulario de la lógica clásica, algunas inferencias válidas en la lógica clásica no son válidas en ella. El término "lógica desviada" a menudo se usa de forma que incluye también las lógicas cuasi-desviadas.

Un problema filosófico que surge de esta variedad de lógicas es si puede haber más de una lógica verdadera. Algunos pensadores prefieren un enfoque local, donde diferentes tipos de lógica se aplican a diferentes áreas. Por ejemplo, los primeros intuicionistas veían la lógica intuicionista como la lógica correcta para las matemáticas, pero permitían la lógica clásica en otros campos. Pero otros, como Michael Dummett, prefieren un enfoque global, diciendo que la lógica intuicionista debería reemplazar a la lógica clásica en todas las áreas.

El monismo es la idea de que solo hay una lógica verdadera. Esto puede significar que solo uno de todos los sistemas lógicos propuestos es correcto, o que el sistema lógico correcto aún no se ha encontrado y es un sistema que unifica todas las lógicas. Los pluralistas, por otro lado, creen que varios sistemas lógicos diferentes pueden ser correctos al mismo tiempo.

Un problema relacionado es si todos estos sistemas formales son realmente "lógicos". Esto es especialmente importante para las lógicas desviadas, que se alejan mucho de las ideas lógicas comunes asociadas a la lógica clásica. Por ejemplo, se ha dicho que la lógica difusa es una lógica solo de nombre, y que debería considerarse un sistema formal no lógico. Esto se debe a que la idea de "grados de verdad" se aleja demasiado de las ideas lógicas más fundamentales. Por lo tanto, no todos están de acuerdo en que todos los sistemas formales que se discuten en este artículo sean realmente "lógicas" en un sentido estricto.

Lógica clásica: La base

La lógica clásica es la forma de lógica más usada en la mayoría de los campos. Este término se refiere principalmente a la lógica proposicional y la lógica de primer orden. La lógica clásica no es un tema independiente dentro de la lógica filosófica. Sin embargo, es importante conocerla bien, ya que muchos de los sistemas lógicos que interesan a la lógica filosófica se entienden como extensiones de la lógica clásica (aceptan sus principios y se basan en ella) o como modificaciones de ella (rechazan algunos de sus principios centrales).

La lógica clásica se creó inicialmente para analizar argumentos matemáticos y solo después se aplicó a otros campos. Por esta razón, no aborda muchos temas importantes en filosofía que no son relevantes para las matemáticas, como la diferencia entre necesidad y posibilidad, entre obligación y permiso, o entre pasado, presente y futuro. Estos y otros temas similares son tratados lógicamente en las diferentes lógicas filosóficas que extienden la lógica clásica.

La lógica clásica por sí misma solo se ocupa de unos pocos conceptos básicos y de cómo estos conceptos ayudan a hacer inferencias válidas. Los conceptos de la lógica proposicional incluyen conectores como "y", "o" y "si-entonces". Lo característico del enfoque clásico de estos conectores es que siguen ciertas leyes, como el principio del tercero excluido, la eliminación de la doble negación, el principio de explosión y la bivalencia de la verdad. Esto diferencia a la lógica clásica de varias lógicas desviadas, que niegan uno o varios de estos principios.

En la lógica de primer orden, las proposiciones (afirmaciones) se forman con partes más pequeñas, como predicados, términos singulares y cuantificadores. Los términos singulares se refieren a objetos, y los predicados expresan propiedades de los objetos o relaciones entre ellos. Los cuantificadores son una forma formal de decir "para algunos" y "para todos". Se usan para expresar si los predicados se aplican a algunos o a todos los elementos de un grupo. En la lógica de primer orden, solo se puede hablar de cantidades de individuos, no de propiedades, a diferencia de las lógicas de orden superior.

Lógicas extendidas: Ampliando la lógica clásica

Lógica modal alética: Posibilidad y necesidad

La lógica modal alética ha sido muy importante en la lógica y la filosofía. Ofrece una forma lógica de expresar lo que es posible o necesariamente verdadero. Es una extensión de la lógica de primer orden, que por sí misma solo puede expresar lo que es simplemente verdadero.

Esta extensión se logra introduciendo dos nuevos símbolos: para la posibilidad y para la necesidad. Estos símbolos se usan para modificar afirmaciones. Por ejemplo, si 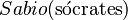significa "Sócrates es sabio", entonces 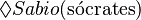expresa "es posible que Sócrates sea sabio".

Para integrar estos símbolos en el sistema lógico, se añaden varios axiomas (reglas básicas) a los de la lógica de primer orden. Estos axiomas rigen cómo se comportan lógicamente estos símbolos, determinando cómo la validez de una inferencia depende de su presencia. Suelen incluir la idea de que si una afirmación es necesaria, entonces su negación es imposible. Esto significa que es lo mismo que 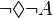. Otro principio es que si algo es necesario, entonces también debe ser posible. Esto significa que 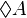se deduce de .

Hay desacuerdo sobre cuáles son los axiomas exactos que rigen la lógica modal. Las diferentes formas de lógica modal a menudo se presentan como una jerarquía de sistemas. Los sistemas más básicos, como el sistema K, incluyen solo los axiomas más fundamentales. Otros sistemas, como el popular sistema S5, se construyen sobre ellos añadiendo axiomas adicionales. En este sentido, el sistema K es una extensión de la lógica de primer orden, y el sistema S5 es una extensión del sistema K.

Discusiones importantes en la lógica filosófica se refieren a qué sistema de lógica modal es el correcto. Generalmente, es útil tener el sistema más fuerte posible para poder hacer muchas inferencias diferentes. Pero esto puede llevar a que algunas de estas inferencias adicionales contradigan ideas modales básicas en casos específicos. Esto a menudo motiva la elección de un sistema de axiomas más básico.

La semántica de mundos posibles es una forma muy influyente de entender la lógica modal, y se relaciona con el sistema S5. Una semántica formal de un lenguaje describe las condiciones bajo las cuales las oraciones de ese lenguaje son verdaderas o falsas. Las semánticas formales son clave para entender la validez de las inferencias. Proporcionan criterios claros para saber cuándo una inferencia es válida: una inferencia es válida si y solo si siempre que sus premisas son verdaderas, su conclusión también lo es. La semántica formal especifica si las oraciones son verdaderas o falsas.

La semántica de mundos posibles explica las condiciones de verdad de las oraciones en lógica modal usando la idea de "mundos posibles". Un mundo posible es una forma completa y coherente en que las cosas podrían haber sido. Desde este punto de vista, una oración con el operador (posibilidad) es verdadera si es verdadera en al menos un mundo posible. Una oración con el operador (necesidad) es verdadera si es verdadera en todos los mundos posibles.

Así, la oración 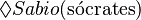(es posible que Sócrates sea sabio) es verdadera porque hay al menos un mundo donde Sócrates es sabio. Pero 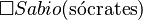(es necesario que Sócrates sea sabio) es falsa, ya que Sócrates no es sabio en todos los mundos posibles. La semántica de mundos posibles ha sido criticada porque parece ser circular. Esto se debe a que los mundos posibles se definen usando términos modales, es decir, como formas en que las cosas podrían haber sido. Por lo tanto, usa expresiones modales para determinar la verdad de oraciones que contienen expresiones modales.

Lógica deóntica: Obligación y permiso

La lógica deóntica extiende la lógica clásica al campo de la ética. En ética, los conceptos de obligación y permiso son muy importantes. Se refieren a qué acciones una persona debe hacer o tiene permitido hacer. La lógica deóntica suele expresar estas ideas con los operadores y .

Por ejemplo, si representa la afirmación "Ramírez sale a correr", entonces 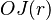significa que Ramírez tiene la obligación de salir a correr. Y 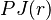significa que Ramírez tiene permiso para salir a correr.

La lógica deóntica está muy relacionada con la lógica modal alética. Los axiomas que rigen el comportamiento lógico de sus operadores son idénticos. Esto significa que la obligación y el permiso se comportan de la misma manera que la necesidad y la posibilidad en cuanto a las inferencias válidas. Por esta razón, a veces incluso se usan los mismos símbolos como operadores.

Al igual que en la lógica modal alética, hay un debate en la lógica filosófica sobre cuál es el sistema de axiomas correcto para expresar las ideas comunes que rigen las inferencias deónticas. Pero los argumentos y ejemplos son un poco diferentes, ya que los significados de estos operadores son distintos. Por ejemplo, una idea común en ética es que si alguien tiene la obligación de hacer algo, entonces automáticamente también tiene el permiso para hacerlo. Esto se puede expresar formalmente con el esquema axiomático .

Otra cuestión de interés para la lógica filosófica es la relación entre la lógica modal alética y la lógica deóntica. Un principio que se discute a menudo es que el deber implica el poder. Esto significa que una persona solo puede tener la obligación de hacer algo si es posible que lo haga. Expresado formalmente: .

Lógica temporal: El tiempo en la lógica

La lógica temporal, también llamada lógica tensional, usa herramientas lógicas para expresar relaciones de tiempo. En su forma más simple, tiene un operador para decir que algo ocurrió en un momento y otro para decir que algo está ocurriendo todo el tiempo. Estos dos operadores se comportan de la misma manera que los operadores de posibilidad y necesidad en la lógica modal alética.

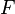Como la diferencia entre el pasado y el futuro es muy importante para los seres humanos, estos operadores a menudo se modifican para tener en cuenta esta diferencia. La lógica tensional de Arthur Prior, por ejemplo, usa cuatro de estos operadores: (fue el caso que...), (será el caso que...), 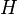(siempre ha sido el caso que...) y 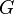(siempre será el caso que...). Así, para expresar que siempre lloverá en Londres se podría usar .

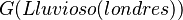Hay varios axiomas para determinar qué inferencias son válidas según los operadores que aparecen en ellas. Según ellos, por ejemplo, se puede deducir 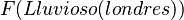(lloverá en Londres en algún momento) de 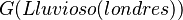. En formas más complejas de la lógica temporal, también se definen operadores binarios que conectan dos afirmaciones, por ejemplo, para expresar que algo ocurre hasta que otra cosa ocurre.

La lógica modal temporal se puede traducir a la lógica clásica de primer orden tratando el tiempo como un término singular y aumentando en uno el número de argumentos de los predicados. Por ejemplo, la oración de lógica temporal 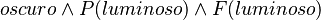(es oscuro, era luminoso y volverá a ser luminoso) se puede traducir a la lógica pura de primer orden como .

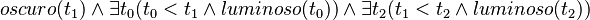Aunque se ven enfoques similares en la física, los lógicos generalmente prefieren un tratamiento autónomo del tiempo usando operadores. Esto también se parece más a los lenguajes naturales, que en su mayoría usan la gramática, por ejemplo, la conjugación de verbos, para expresar el pasado o el futuro de los eventos.

Lógica epistémica: Conocimiento y creencia

La lógica epistémica es un tipo de lógica modal aplicada al campo de la epistemología (el estudio del conocimiento). Su objetivo es entender la lógica del conocimiento y la creencia. Los operadores modales que expresan conocimiento y creencia suelen representarse con los símbolos 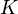(de knows, saber) y (de believes, creer).

Así, si 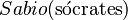representa la afirmación "Sócrates es sabio", entonces 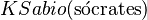expresa "la persona sabe que Sócrates es sabio". Y 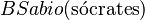expresa "la persona cree que Sócrates es sabio". Los axiomas que rigen estos operadores se formulan para expresar varios principios sobre el conocimiento.

Por ejemplo, el esquema axiomático expresa que siempre que algo se sabe, entonces es verdadero. Esto refleja la idea de que solo se puede saber lo que es verdadero; de lo contrario, no es conocimiento sino otro estado mental. Otra idea sobre el conocimiento es que cuando una persona sabe algo, también sabe que lo sabe. Esto se puede expresar con el esquema axiomático 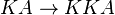. Un principio adicional que conecta el conocimiento y la creencia establece que el conocimiento implica la creencia, es decir, .

La lógica epistémica dinámica es una forma diferente de lógica epistémica que se enfoca en situaciones donde hay cambios en la creencia y el conocimiento.

Lógicas de orden superior: Cuantificando propiedades

Las lógicas de orden superior amplían la lógica de primer orden al incluir nuevas formas de cuantificación. En la lógica de primer orden, la cuantificación se limita a los términos singulares. Se puede usar para hablar sobre si un predicado se aplica a algunos o a todos los elementos de un grupo. Así, se pueden expresar afirmaciones como 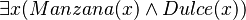(hay algunas manzanas que son dulces).

En las lógicas de orden superior, se permite la cuantificación no solo sobre individuos, sino también sobre propiedades (predicados). De esta manera, es posible expresar, por ejemplo, que ciertos individuos comparten algunas o todas sus propiedades, como en 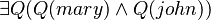(hay algunas cualidades que María y Juan comparten).

Debido a estos cambios, las lógicas de orden superior tienen más poder para expresar ideas que la lógica de primer orden. Esto puede ser útil para las matemáticas de varias maneras, ya que diferentes teorías matemáticas se expresan de forma mucho más simple en la lógica de orden superior que en la lógica de primer orden. Por ejemplo, la aritmética de Peano y la teoría de conjuntos de Zermelo-Fraenkel necesitan un número infinito de axiomas para expresarse en la lógica de primer orden. Pero pueden expresarse en la lógica de segundo orden con solo unos pocos axiomas.

Pero a pesar de esta ventaja, la lógica de primer orden todavía se usa mucho más que la lógica de orden superior. Una razón es que la lógica de orden superior es incompleta. Esto significa que, para las teorías formuladas en la lógica de orden superior, no es posible demostrar todas las afirmaciones verdaderas que pertenecen a la teoría en cuestión.

Otra desventaja está relacionada con las ideas adicionales sobre la existencia que implican las lógicas de orden superior. A menudo se dice que usar el cuantificador existencial implica que las entidades sobre las que se aplica ese cuantificador existen. En la lógica de primer orden, esto se refiere solo a los individuos, lo que generalmente se considera una idea de existencia sin problemas. En la lógica de orden superior, la cuantificación también afecta a las propiedades y relaciones. Esto a menudo se interpreta como que la lógica de orden superior implica una forma de platonismo, es decir, la idea de que las propiedades y relaciones universales existen además de los individuos.

Lógicas desviadas: Desafiando la lógica clásica

Lógica intuicionista: La verdad es verificable

La lógica intuicionista es una versión más estricta de la lógica clásica. Es más estricta porque ciertas reglas de inferencia usadas en la lógica clásica no son válidas en ella. Esto se refiere específicamente al principio del tercero excluido y la eliminación de la doble negación.

El principio del tercero excluido dice que para cada afirmación, o ella o su negación es verdadera. Formalmente: 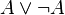. La ley de la eliminación de la doble negación dice que si una afirmación no es no verdadera, entonces es verdadera, es decir, 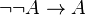. Debido a estas restricciones, muchas pruebas son más complicadas y algunas pruebas que de otro modo serían aceptadas se vuelven imposibles.

Estas modificaciones de la lógica clásica están motivadas por la idea de que la verdad depende de ser verificada a través de una prueba. Esto se ha interpretado como que "verdadero" significa "verificable". Originalmente, esto solo se aplicaba a las matemáticas, pero desde entonces también se ha usado en otros campos.

Según esta interpretación, el principio del tercero excluido implicaría que cada problema matemático tiene una solución en forma de prueba. En este sentido, el rechazo intuicionista del principio del tercero excluido se debe a que no aceptan esta idea. Esta postura también se puede expresar diciendo que no hay verdades que no hayan sido experimentadas o que estén más allá de la verificación. En este sentido, la lógica intuicionista está motivada por una forma de idealismo metafísico. Aplicada a las matemáticas, afirma que los objetos matemáticos existen solo en la medida en que se construyen en la mente.

Lógica libre: Manejando lo que no existe

La lógica libre no acepta algunas de las ideas sobre la existencia que se encuentran en la lógica clásica. En la lógica clásica, cada término singular (como un nombre) debe referirse a un objeto que existe. Esto a menudo se entiende como una afirmación de que la entidad nombrada existe. Pero en el lenguaje diario, usamos muchos nombres que no se refieren a entidades existentes, como "Papá Noel" o "Pegaso". Esto podría impedir que estas áreas del lenguaje se traten de forma lógica.

La lógica libre evita estos problemas al permitir afirmaciones con términos singulares que no se refieren a nada. Esto se aplica a los nombres propios, así como a las descripciones definidas y a las expresiones que funcionan como nombres. Los cuantificadores, por otro lado, se tratan de la manera habitual, abarcando solo lo que existe. Esto permite que expresiones como 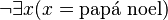(Papá Noel no existe) sean verdaderas, aunque son contradictorias en la lógica clásica.

También implica que ciertas formas válidas de inferencia que se encuentran en la lógica clásica no son válidas en la lógica libre. Por ejemplo, en la lógica clásica se puede inferir de 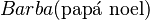(Papá Noel tiene barba) que 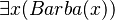(algo tiene barba), pero no en la lógica libre. En la lógica libre, a menudo se usa un predicado de existencia para indicar si un término singular se refiere a un objeto que existe o no. Pero el uso de predicados de existencia es un tema de debate. A menudo se oponen a ellos basándose en la idea de que es necesario existir para que cualquier predicado se aplique a un objeto. En este sentido, la existencia misma no puede ser un predicado.

Karel Lambert, quien acuñó el término "lógica libre", ha sugerido que la lógica libre puede entenderse como una generalización de la lógica clásica de predicados, de la misma manera que la lógica de predicados es una generalización de la lógica aristotélica. Desde este punto de vista, la lógica clásica de predicados introduce predicados con una extensión vacía, mientras que la lógica libre introduce términos singulares de cosas que no existen.

Un problema importante para la lógica libre es cómo determinar el valor de verdad de las expresiones que contienen términos singulares vacíos, es decir, cómo crear una semántica formal para la lógica libre. La semántica formal de la lógica clásica puede definir la verdad de sus expresiones en función de a qué se refieren. Pero esta opción no se puede aplicar a todas las expresiones de la lógica libre, ya que no todas tienen una referencia.

Se discuten a menudo tres enfoques generales para este problema: la semántica negativa, la semántica positiva y la semántica neutral.

• La semántica negativa sostiene que todas las afirmaciones básicas que contienen términos vacíos son falsas. Desde este punto de vista, la expresión 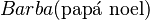es falsa.
• La semántica positiva permite que al menos algunas expresiones con términos vacíos sean verdaderas. Esto generalmente incluye declaraciones de identidad, como . Algunas versiones introducen un segundo grupo externo para los objetos que no existen, que luego se usa para determinar los valores de verdad correspondientes.
• Las semánticas neutrales, por otro lado, sostienen que las afirmaciones básicas que contienen términos vacíos no son ni verdaderas ni falsas. Esto a menudo se entiende como una lógica trivalente, es decir, que se introduce un tercer valor de verdad además de verdadero y falso para estos casos.

Lógicas plurivalentes: Más de dos valores de verdad

Las lógicas plurivalentes son lógicas que permiten más de dos valores de verdad. Rechazan una de las ideas centrales de la lógica clásica: el principio de bivalencia de la verdad (que una afirmación es solo verdadera o falsa).

Las versiones más simples de las lógicas plurivalentes son las lógicas trivalentes: contienen un tercer valor de verdad. En la lógica trivalente de Stephen Cole Kleene, por ejemplo, este tercer valor de verdad es "indefinido". Según la lógica cuadrivalente de Nuel Belnap, hay cuatro posibles valores de verdad: "verdadero", "falso", "ni verdadero ni falso" y "tanto verdadero como falso". Esto puede interpretarse, por ejemplo, como la información que se tiene sobre si un estado se da: información de que se da, información de que no se da, ninguna información e información contradictoria.

Una de las formas más extremas de la lógica plurivalente es la lógica difusa. Permite que la verdad exista en cualquier grado entre 0 y 1. El 0 corresponde a completamente falso, el 1 a completamente verdadero, y los valores intermedios corresponden a cierto grado de verdad, por ejemplo, como un poco verdadero o muy verdadero. A menudo se usa para tratar expresiones vagas en el lenguaje natural. Por ejemplo, decir que "Petr es joven" encaja mejor (es decir, es "más verdadero") si "Petr" se refiere a un niño de tres años que si se refiere a una persona de 23 años.

Las lógicas plurivalentes con un número finito de valores de verdad pueden definir sus conectores lógicos mediante tablas de verdad, al igual que la lógica clásica. La diferencia es que estas tablas de verdad son más complejas, ya que se deben considerar más entradas y salidas posibles. En la lógica trivalente de Kleene, por ejemplo, las entradas "verdadero" e "indefinido" para el operador de conjunción 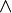dan como resultado la salida "indefinido". Las entradas "falso" e "indefinido", por otro lado, dan como resultado "falso".

Lógicas paraconsistentes: Manejando contradicciones

Las lógicas paraconsistentes son sistemas lógicos que pueden manejar contradicciones sin llevar a un absurdo total. Lo consiguen evitando el principio de explosión que se encuentra en la lógica clásica. Según el principio de explosión, cualquier cosa se deduce de una contradicción.

Esto se debe a dos reglas de inferencia que son válidas en la lógica clásica: la introducción de la disyunción y el silogismo disyuntivo. Según la introducción de la disyunción, cualquier afirmación puede introducirse en forma de "o" cuando se combina con una afirmación verdadera. Entonces, dado que es cierto que "el sol es más grande que la luna", se puede inferir que "el sol es más grande que la luna o España está controlada por conejos espaciales". Según el silogismo disyuntivo, se puede inferir que una de estas afirmaciones "o" es verdadera si la otra es falsa. Entonces, si el sistema lógico también contiene la negación de esta afirmación, es decir, que "el sol no es más grande que la luna", entonces es posible inferir cualquier afirmación de este sistema, como la afirmación de que "España está controlada por conejos espaciales". Las lógicas paraconsistentes evitan esto usando reglas de inferencia diferentes que hacen que las inferencias según el principio de explosión no sean válidas.

Una motivación importante para usar lógicas paraconsistentes es el dialeteismo. Esta es la creencia de que las contradicciones no solo aparecen en las teorías por errores, sino que la realidad misma es contradictoria. Y que las contradicciones dentro de las teorías son necesarias para reflejar la realidad con precisión. Sin lógicas paraconsistentes, el dialeteismo no tendría sentido, ya que todo sería tanto verdadero como falso. Las lógicas paraconsistentes permiten mantener las contradicciones en un lugar, sin que todo el sistema "explote". Pero incluso con este ajuste, el dialeteismo sigue siendo muy debatido.

Otra motivación para la lógica paraconsistente es proporcionar una lógica para las discusiones y las creencias de grupo. En estas situaciones, el grupo en su conjunto puede tener creencias inconsistentes si sus diferentes miembros no están de acuerdo.

Lógica relevante: La importancia de la conexión

La lógica relevante es un tipo de lógica paraconsistente. Como tal, también evita el principio de explosión, aunque esta no suele ser la razón principal de su existencia. En cambio, suele formularse con el objetivo de evitar ciertas aplicaciones poco intuitivas de la afirmación "si... entonces..." (condicional material) que se encuentran en la lógica clásica.

La lógica clásica define el condicional material de forma puramente funcional de verdad. Es decir, 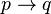es falso si 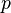es verdadero y 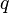es falso, pero por lo demás es verdadero en todos los casos. Según esta definición formal, no importa si 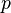y 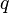están relacionadas de alguna manera. Por ejemplo, el condicional material "si todos los limones son rojos, entonces hay una tormenta de arena dentro de la Ópera de Sídney" es verdadero, aunque las dos afirmaciones no tienen relación entre sí.

El hecho de que este uso de condicionales materiales es muy poco intuitivo también se refleja en la lógica informal, que clasifica tales inferencias como falacias de relevancia. La lógica de la relevancia intenta evitar estos casos exigiendo que, para que un condicional material sea verdadero, su primera parte (antecedente) debe ser relevante para la segunda parte (consecuente).

Una dificultad que enfrenta este tema es que la relevancia suele pertenecer al contenido de las afirmaciones, mientras que la lógica solo se ocupa de los aspectos formales. Este problema se aborda parcialmente mediante el principio de compartición de variables. Establece que el antecedente y el consecuente tienen que compartir una variable proposicional. Este sería el caso, por ejemplo, en 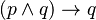pero no en 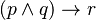. Una preocupación estrechamente relacionada con la lógica relevante es que las inferencias deben seguir el mismo requisito de relevancia, es decir, que es un requisito necesario de las inferencias válidas que sus premisas sean relevantes para su conclusión.

Véase también

En inglés: Philosophical logic Facts for Kids

• Filosofía de la lógica
• Filosofía de la mente