Notación científica para niños
La notación científica es una forma especial de escribir números que son muy grandes o muy pequeños. Imagina que tienes que escribir la distancia a una estrella o el tamaño de un átomo; ¡serían números con muchísimos ceros! La notación científica nos ayuda a escribir estas cantidades de forma más corta y fácil de entender.
Esta forma de escribir números se basa en potencias de 10. Un número en notación científica se ve así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a\ \times\ 10^{n} .
- La letra a (llamada coeficiente o mantisa) es un número que está entre 1 y 10 (puede ser 1, pero siempre menor que 10).
- La letra n (llamada exponente u orden de magnitud) es un número entero (puede ser positivo, negativo o cero).
Esta manera abreviada es muy útil en ciencias como la física y la química, donde se usan mucho estos valores extremos.
Contenido
¿Qué es la mantisa y el orden de magnitud?
Cuando escribimos un número en notación científica, como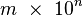 
, tenemos dos partes importantes:
- La mantisa (m): Es un número decimal que tiene una sola cifra antes del punto decimal, y esa cifra no puede ser cero (por ejemplo, 5.2, 4.59, 6.903).
- El orden de magnitud (
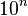): Es una potencia de 10, donde el exponente n es un número entero.
Aquí tienes algunos ejemplos para entenderlo mejor:
- 520 se escribe como 5.2 × 102 (porque 5.2 multiplicado por 100 es 520).
- -45.9 se escribe como -4.59 × 101.
- 575,230,000,000,000 se escribe como 5.7523 × 1014.
- 0.0523 se escribe como 5.23 × 10-2 (porque 5.23 dividido por 100 es 0.0523).
- 0.0000000000000006903 se escribe como 6.903 × 10−16.
El exponente nos dice cuántos lugares debemos mover el punto decimal. Si el exponente es positivo, movemos el punto a la derecha. Si es negativo, lo movemos a la izquierda.
Ejemplos de números en notación científica
La notación científica es muy útil para expresar medidas en ciencia:
- La masa de un electrón es aproximadamente 9.11 × 10-31 kg. ¡Es un número increíblemente pequeño!
- La constante de Avogadro (que representa una cantidad muy grande de partículas) es 6.02 × 1023.
- La mayor distancia observable en el universo es de unos 7.4 × 1026 metros.
¿Quién inventó la notación científica?
.jpg)
Uno de los primeros en intentar representar números extremadamente grandes fue el matemático griego Arquímedes en el siglo III a.C. En su libro El contador de arena, él imaginó un sistema para calcular cuántos granos de arena se necesitarían para llenar el universo. Para esto, tuvo que encontrar una manera de escribir números gigantes. El número que estimó fue de 1063 granos.
Más tarde, la idea de representar números con una parte decimal y una potencia de 10 (lo que hoy llamamos "coma flotante" en las computadoras) fue propuesta por personas como Leonardo Torres y Quevedo en 1914 y Konrad Zuse en 1936.
Tipos de notación científica
Existen algunas variaciones de la notación científica:
Notación estándar
En la notación científica estándar, la mantisa (el número antes del "x 10") siempre es mayor o igual a 1 y menor que 10. Por ejemplo, 350 se escribe como 3.5 × 102. Esta es la forma más común y nos permite comparar fácilmente el tamaño de los números.
Notación E (exponencial)
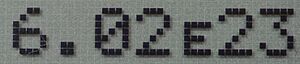
Muchas calculadoras y programas de computadora usan una forma simplificada de la notación científica llamada "notación E". Como no pueden mostrar los exponentes pequeños arriba (como 107), usan la letra "E" (o "e") para separar la mantisa del exponente. Así, "mEn" significa "m multiplicado por 10 elevado a n".
Por ejemplo:
- 6.0221415E23 es lo mismo que 6.0221415 × 1023.
- 1.785E5 es igual a 1.785 × 105.
Es importante saber que la letra "E" aquí no tiene nada que ver con la constante matemática "e" (que es un número diferente).
Notación de ingeniería
La notación de ingeniería es similar a la notación científica, pero el exponente de 10 siempre es un múltiplo de 3 (como 3, 6, 9, -3, -6, etc.). Esto hace que la mantisa sea un número entre 1 y 1000. Esta notación es muy útil porque se relaciona directamente con los prefijos del SI (Sistema Internacional de Unidades), como "kilo" (103), "mega" (106), "mili" (10-3) o "nano" (10-9).
Por ejemplo, 12.5 × 10-9 metros se puede leer como "doce punto cinco nanómetros" (12.5 nm).
¿Por qué es útil la notación científica?
La notación científica es muy práctica por varias razones:
- Simplifica números grandes y pequeños: Evita escribir muchísimos ceros, haciendo los números más fáciles de leer y manejar.
- Facilita cálculos: Es más sencillo multiplicar o dividir números muy grandes o pequeños cuando están en esta forma.
- Muestra las cifras importantes: Nos ayuda a ver rápidamente cuáles son los dígitos que realmente importan en una medida (las cifras significativas).
- Compara tamaños: Permite comparar rápidamente el tamaño de diferentes cantidades, incluso si son muy diferentes.
Cifras significativas
Una gran ventaja de la notación científica es que nos ayuda a saber cuántas cifras significativas tiene un número. En la notación científica estándar, todos los dígitos que se muestran son importantes. Por ejemplo, la velocidad de la luz es 2.99792458 × 108 m/s. Todos esos dígitos son significativos.
Comparación de órdenes de magnitud
La notación científica nos permite comparar el tamaño de diferentes cosas de forma rápida. Por ejemplo:
Para ver cuántas veces es más grande el protón que el electrón, solo necesitamos comparar los exponentes de 10: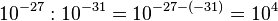 
Esto significa que el protón es aproximadamente 10,000 veces (o 104 veces) más masivo que el electrón.
¿Cómo transformar números a notación científica?
Para escribir un número en notación científica estándar, debemos mover el punto decimal hasta que solo quede una cifra diferente de cero a la izquierda del punto. El número de veces que movemos el punto nos dará el exponente de 10.
Tomemos el número 253756.42: 1. Queremos que la mantisa esté entre 1 y 10. Si movemos el punto, el número sería 2.5375642. 2. ¿Cuántos lugares movimos el punto? Lo movimos 5 lugares hacia la izquierda. 3. Por lo tanto, el exponente es 5. Así, 253756.42 se convierte en 2.5375642 × 105.
Veamos otro ejemplo con un número pequeño: 0.0000000475 1. Queremos que la mantisa esté entre 1 y 10. Si movemos el punto, el número sería 4.75. 2. ¿Cuántos lugares movimos el punto? Lo movimos 8 lugares hacia la derecha. 3. Cuando movemos el punto a la derecha, el exponente es negativo. Así, 0.0000000475 se convierte en 4.75 × 10−8.
Operaciones con notación científica
Podemos sumar, restar, multiplicar, dividir y potenciar números en notación científica.
Suma y resta
Para sumar o restar números en notación científica, los exponentes de 10 deben ser iguales. Si no lo son, debes ajustar uno de los números para que tengan el mismo exponente.
Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {4.2\cdot 10^{7}} + {3.5\cdot 10^{5}} Primero, hacemos que los exponentes sean iguales. Convertimos 3.5 × 105 a un número con 107: 3.5 × 105 = 0.035 × 107 Ahora sumamos: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {4.2\cdot 10^{7}} + {0.035\cdot 10^{7}} = {(4.2 + 0.035)\cdot 10^{7}} = {4.235\cdot 10^{7}}
Multiplicación
Para multiplicar, multiplicamos las mantisas y sumamos los exponentes.
Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {(6.5\cdot 10^{8})}\cdot {(3.2\cdot 10^{5})} Multiplicamos las mantisas (6.5 × 3.2 = 20.8) y sumamos los exponentes (8 + 5 = 13): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {20.8\cdot 10^{13}} Luego, ajustamos a la notación estándar (la mantisa debe ser entre 1 y 10):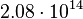 
División
Para dividir, dividimos las mantisas y restamos los exponentes.
Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {(8\cdot 10^{17})} : {(2\cdot 10^{9})} Dividimos las mantisas (8 / 2 = 4) y restamos los exponentes (17 - 9 = 8): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {4\cdot 10^{8}}
Potenciación
Para elevar un número en notación científica a una potencia, elevamos la mantisa a esa potencia y multiplicamos el exponente de 10 por esa potencia.
Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {(2\cdot 10^{6})^4} Elevamos la mantisa (24 = 16) y multiplicamos los exponentes (6 × 4 = 24): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {16\cdot 10^{24}} Luego, ajustamos a la notación estándar: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {1.6\cdot 10^{25}}
Radicación
Para sacar la raíz de un número en notación científica, a veces es útil ajustar el exponente para que sea un múltiplo del índice de la raíz. Luego, sacamos la raíz de la mantisa y dividimos el exponente por el índice de la raíz.
Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{1.6\cdot 10^{27}} Podemos reescribir 1.6 × 1027 como 16 × 1026 para que el exponente (26) sea par y fácil de dividir por 2 (la raíz cuadrada). Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{16\cdot 10^{26}} = \sqrt{16}\cdot 10^{26/2} = 4\cdot 10^{13}
Véase también
En inglés: Scientific notation Facts for Kids
