John Horton Conway para niños
Datos para niños John Horton Conway |
||
|---|---|---|
_(2).jpg) John Horton Conway en 2005
|
||
| Información personal | ||
| Nacimiento | 26 de diciembre de 1937 Liverpool (Reino Unido) |
|
| Fallecimiento | 11 de abril de 2020 Nuevo Brunswick (Nueva Jersey, Estados Unidos) |
|
| Causa de muerte | COVID-19 | |
| Residencia | Nuevo Brunswick | |
| Nacionalidad | Británica | |
| Lengua materna | Inglés | |
| Familia | ||
| Padres | Cyril Horton Conway Agnes Boyce |
|
| Educación | ||
| Educado en | Universidad de Cambridge (hasta 1962) | |
| Supervisor doctoral | Harold Davenport | |
| Información profesional | ||
| Ocupación | Matemático y profesor universitario | |
| Área | Teoría de grupos, teoría de juegos combinatorios, matemáticas, teoría de números, teoría de juegos, teoría de nudos y juego matemático | |
| Empleador |
|
|
| Estudiantes doctorales | Richard Ewen Borcherds | |
| Obras notables |
|
|
| Miembro de |
|
|
| Distinciones |
|
|
John Horton Conway (nacido en Liverpool, Reino Unido, el 26 de diciembre de 1937 y fallecido en Nuevo Brunswick, Nueva Jersey, Estados Unidos, el 11 de abril de 2020) fue un matemático británico muy creativo. Se especializó en varias ramas de las matemáticas, como la teoría de grupos, la teoría de nudos, la teoría de números y la teoría de juegos.
Conway creció en Liverpool y pasó la primera parte de su carrera en la Universidad de Cambridge. Luego se mudó a los Estados Unidos para trabajar en la Universidad de Princeton. Falleció a los 82 años debido a complicaciones de COVID-19.
Contenido
Biografía de John Horton Conway
John Conway nació el 26 de diciembre de 1937 en Liverpool. Sus padres fueron Cyril Horton Conway y Agnes Boyce. Desde muy pequeño, mostró un gran interés por las matemáticas. A los 11 años, ya soñaba con ser matemático.
Después de terminar la escuela, estudió matemáticas en la Universidad de Cambridge. Al principio, era un adolescente un poco tímido. Sin embargo, al entrar a Cambridge, decidió cambiar y volverse más abierto. Este cambio hizo que lo conocieran como "el matemático más carismático del mundo".
Conway se graduó en 1959 y comenzó a investigar sobre la teoría de números. Resolvió un problema difícil que había propuesto su profesor, Harold Davenport. También se interesó por los números infinitos. Durante sus estudios, le gustaba mucho jugar backgammon. Obtuvo su doctorado en 1964 y se convirtió en profesor en Cambridge. En 1986, se fue a la Universidad de Princeton, donde fue profesor de matemáticas.
El Juego de la Vida de Conway
Conway es muy famoso por inventar el Juego de la Vida. Este fue uno de los primeros ejemplos de un autómata celular. Al principio, Conway hacía sus experimentos con lápiz y papel, mucho antes de que existieran las computadoras personales.
Desde que Martin Gardner presentó el juego en la revista Scientific American en 1970, se han creado cientos de programas de computadora, sitios web y artículos sobre él. Es un juego muy popular en las matemáticas recreativas. Existe una wiki completa dedicada a este juego. El Juego de la Vida ha sido muy útil en los laboratorios de computación. Ayuda a entender ideas teóricas y es un buen ejercicio para programar.
Aunque el juego lo hizo famoso, a Conway no siempre le gustaba que eclipsara sus otros trabajos importantes. Sin embargo, el Juego de la Vida ayudó a crear una nueva rama de las matemáticas: el estudio de los autómatas celulares. Este juego es tan complejo que puede realizar cálculos como una computadora.
Colaboración con Martin Gardner
La carrera de Conway estuvo muy ligada a la de Martin Gardner, un escritor que divulgaba las matemáticas en la revista Scientific American. Cuando Gardner publicó el Juego de la Vida de Conway en su columna en 1970, fue la columna más leída y Conway se hizo famoso al instante.
Gardner y Conway se escribieron por primera vez a finales de los años 50. A lo largo de los años, Gardner escribió a menudo sobre los aspectos divertidos del trabajo de Conway. Por ejemplo, habló sobre el juego de Brotes de Conway, el Hackenbush y su problema del ángel. También explicó los números surreales de Conway en una de sus columnas.
Conway era un miembro importante del grupo de matemáticos de Martin Gardner. Lo visitaba a menudo y le enviaba cartas largas con sus investigaciones. En una visita en 1976, Gardner le pidió información sobre las teselaciones de Penrose, que eran un descubrimiento reciente. Conway había encontrado muchas de las propiedades principales de estos mosaicos. Gardner usó estos resultados para presentar los mosaicos de Penrose al mundo en su columna de 1977. La portada de esa revista, con los mosaicos de Penrose, se basó en un dibujo de Conway.
Cada dos años se realizan conferencias llamadas Gathering 4 Gardner para celebrar el legado de Martin Gardner. Conway era un orador frecuente en estos eventos, donde hablaba de diferentes temas de matemáticas recreativas.
Áreas de Investigación de Conway
Teoría de Juegos Combinatorios
Conway fue muy conocido por sus aportes a la teoría de juegos combinatorios (CGT). Esta teoría estudia los juegos donde los jugadores se turnan y tienen información completa. La desarrolló junto a Elwyn Berlekamp y Richard Guy. Juntos escribieron el libro Winning Ways for your Mathematical Plays. Conway también escribió On Numbers and Games (ONAG), que explica las bases matemáticas de esta teoría.
Inventó juegos como los brotes y el Phutball. Analizó muchos otros juegos y rompecabezas, como el cubo Soma y el solitario de clavijas. También propuso el problema del ángel, que fue resuelto en 2006.
Creó un nuevo sistema de números, los números surreales, que están relacionados con ciertos juegos. También inventó una forma de escribir números muy grandes, llamada notación de flechas encadenadas de Conway.
Geometría y Formas
A mediados de los años 60, Conway y Michael Guy descubrieron que existen 64 policoras uniformes convexas (formas geométricas en cuatro dimensiones). También sugirió un sistema para describir poliedros (formas con caras planas) llamado notación de poliedros de Conway.
En el estudio de los mosaicos, ideó el criterio de Conway. Este criterio ayuda a identificar rápidamente qué formas pueden cubrir un plano sin dejar huecos.
Investigó las estructuras de puntos en dimensiones más altas. Fue el primero en determinar el grupo de simetría de la celosía Leech, una estructura matemática compleja.
Nudos y Topología
En la teoría de nudos, Conway creó una variación del polinomio de Alexander y un nuevo invariante llamado polinomio de Conway. Este concepto fue muy importante para el estudio de los polinomios de nudos en los años 80.
Conway también desarrolló la teoría de nudos y creó un sistema para clasificar nudos, conocido como notación de Conway. Corrigió errores en tablas de nudos antiguas y las amplió. El nudo de Conway lleva su nombre.
Teoría de Grupos
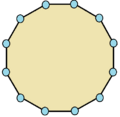
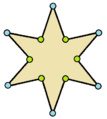
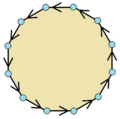
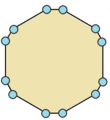
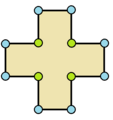
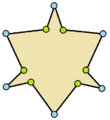
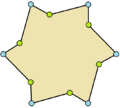
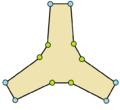
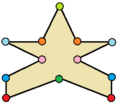
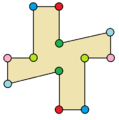
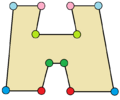
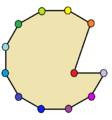
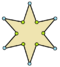
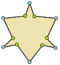
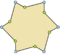
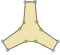
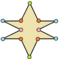
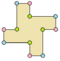
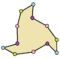
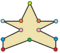
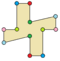
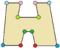
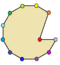
| Ejemplos de dodecágonos según su simetría | ||||||
|---|---|---|---|---|---|---|
 r24 |
||||||
 d12 |
 g12 |
 p12 |
 i8 |
|||
 d6 |
 g6 |
 p6 |
 d4 |
 g4 |
 p4 |
|
 g3 |
 d2 |
 g2 |
 p2 |
|||
 a1 |
||||||
| Conway clasificó estas simetrías usando una letra y el orden de la simetría a continuación. Asignó la letra r al grupo de simetría de la figura regular; y en el caso de los subgrupos utilizó la letra d (de diagonal) para las figuras con ejes de simetría solo a través de sus vértices; p para figuras con ejes de simetría solo a través de ejes perpendiculares a sus lados; i para figuras con ejes de simetría tanto a través de vértices como a través de centros de lados; y g para aquellas figuras solo con simetría rotacional. Con a1 se etiquetan aquellas figuras con ausencia de simetría. Los tipos de simetrías más bajos permiten disponer de uno o más grados de libertad para definir distintas figuras irregulares. Solo el subgrupo g12 no tiene grados de libertad, pero puede verse como un grafo dirigido | ||||||
Conway fue el autor principal del Atlas de grupos finitos, un libro que describe las propiedades de muchos grupos matemáticos. Junto con sus colegas, construyó las primeras representaciones de algunos grupos esporádicos. Descubrió tres grupos esporádicos basados en la simetría de la celosía Leech, que se conocen como grupos de Conway. Su trabajo fue clave para clasificar los grupos finitos simples.
Conway y Norton también formularon una serie de ideas llamadas Monstrous moonshine. Este tema, nombrado por Conway, conecta el grupo monstruo (un grupo matemático muy grande) con las funciones modulares elípticas. Esto unió dos áreas de las matemáticas que antes parecían separadas.
Teoría de Números
Cuando era estudiante, Conway demostró parte de una idea de Edward Waring. Esta idea decía que cualquier número entero se podía escribir como la suma de 37 números elevados a la quinta potencia.
Álgebra
Conway escribió libros y realizó trabajos originales en álgebra. Se centró en los cuaterniones y octoniones. Junto con Neil Sloane, inventó los icosianos.
Algoritmos y Cálculos
Para calcular el día de la semana de cualquier fecha, inventó el algoritmo Doomsday. Este algoritmo es tan sencillo que cualquiera puede hacer los cálculos mentalmente. Conway solía dar la respuesta correcta en menos de dos segundos. Para practicar, tenía su computadora programada para hacerle preguntas con fechas al azar cada vez que se conectaba.
Física Teórica
En 2004, Conway y Simon B. Kochen, otro matemático, demostraron el teorema del libre albedrío. Este teorema es una idea sorprendente sobre la mecánica cuántica. Afirma que si un científico puede elegir libremente qué medir en un experimento, entonces las partículas elementales también deben tener la "libertad" de elegir sus propiedades para que las mediciones coincidan con las leyes de la física. Conway lo explicó así: "si los experimentadores tienen libre albedrío, también lo tienen las partículas elementales".
Premios y Reconocimientos
Conway recibió varios premios importantes, como el Premio Berwick (1971) y el Premio Pólya (LMS) (1987). Fue elegido miembro de la Royal Society en 1981 y de la Academia Estadounidense de Artes y Ciencias en 1992. También ganó el Premio Nemmers en Matemáticas (1998) y el Premio Leroy Steele (2000). Recibió títulos honorarios de la Universidad de Liverpool en 2001 y de la Universidad Alexandru Ioan Cuza de Iași en 2014.
En 2017, la Asociación Matemática Británica le otorgó una membresía honoraria.
Fallecimiento
El 8 de abril de 2020, Conway empezó a tener síntomas de COVID-19. Falleció el 11 de abril en Nuevo Brunswick, Nueva Jersey, a los 82 años.
Libros y Publicaciones Destacadas
- 1971 – Regular algebra and finite machines.
- 1976 – On numbers and games.
- 1979 – On the Distribution of Values of Angles Determined by Coplanar Points (con Paul Erdős, Michael Guy, y H. T. Croft).
- 1979 – Monstrous Moonshine (con Simon P. Norton).
- 1982 – Winning Ways for your Mathematical Plays (con Richard K. Guy y Elwyn Berlekamp).
- 1985 – Atlas of finite groups (con Robert Turner Curtis, Simon Phillips Norton, Richard A. Parker, y Robert Arnott Wilson).
- 1988 – Sphere Packings, Lattices, and Groups (con Neil Sloane).
- 1995 – Minimal-Energy Clusters of Hard Spheres (con Neil Sloane, R. H. Hardin, y Tom Duff).
- 1996 – The Book of Numbers (con Richard K. Guy).
- 1997 – The Sensual (quadratic) Form (con Francis Yein Chei Fung).
- 2002 – On Quaternions and Octonions (con Derek A. Smith).
- 2008 – The Symmetries of Things (con Heidi Burgiel y Chaim Goodman-Strauss).
Galería de imágenes
-
Un cañón de Gosper creando "gliders" en el Juego de la Vida de Conway
-
Dodecágono con simetría completa
-
Dodecágono con simetría d12
-
Dodecágono con simetría g12
-
Dodecágono con simetría p12
-
Dodecágono con simetría i8
-
Dodecágono con simetría d6
-
Dodecágono con simetría g6
-
Dodecágono con simetría p6
-
Dodecágono con simetría d4
-
Dodecágono con simetría g4
-
Dodecágono con simetría p4
-
Dodecágono con simetría g3
-
Dodecágono con simetría d2
-
Dodecágono con simetría g2
-
Dodecágono con simetría p2
-
Dodecágono sin simetría
Véase también
En inglés: John Horton Conway Facts for Kids
- Juego de la vida
- Números surreales
- Constante de Conway
