Geometría analítica para niños
La geometría analítica es una rama de las matemáticas que nos ayuda a estudiar las figuras geométricas de una manera diferente. Imagina que puedes describir un círculo, una línea o cualquier forma usando números y ecuaciones. Eso es lo que hace la geometría analítica.
Esta parte de las matemáticas usa herramientas del álgebra y el análisis matemático junto con un sistema de coordenadas. Gracias a ella, podemos calcular distancias, áreas, dónde se cruzan las figuras, sus ángulos y volúmenes. Es como darle un "mapa de coordenadas" a cada punto de una figura para entenderla mejor.
La geometría analítica comenzó a desarrollarse con las ideas de René Descartes. Luego, matemáticos como Carl Friedrich Gauss y otros la hicieron crecer aún más. Hoy en día, no solo se usa en matemáticas e ingeniería, sino también para planificar estrategias y organizar cosas en muchos campos.
La geometría analítica busca responder dos preguntas principales:
- Si tenemos una figura dibujada en un sistema de coordenadas, ¿cómo podemos encontrar la ecuación que la describe?
- Si tenemos una ecuación, ¿cómo podemos dibujar la figura o el conjunto de puntos que cumplen con esa ecuación?
Por ejemplo, una recta se puede describir con una ecuación como 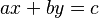 . Las circunferencias y otras figuras llamadas cónicas se describen con ecuaciones un poco más complejas, que tienen números elevados al cuadrado, como
. Las circunferencias y otras figuras llamadas cónicas se describen con ecuaciones un poco más complejas, que tienen números elevados al cuadrado, como 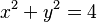 para una circunferencia.
para una circunferencia.
Contenido
Historia de la Geometría Analítica
Orígenes Antiguos
Desde la Antigua Grecia, algunos matemáticos ya usaban ideas parecidas a las coordenadas. Por ejemplo, Menecmo resolvió problemas usando un método que se parecía mucho a la geometría analítica.
Apolonio de Perge, otro matemático griego, también se acercó mucho a esta idea en su obra Cónicas. Él usaba líneas de referencia para describir curvas, de una forma similar a cómo usamos los ejes de coordenadas hoy. Sin embargo, no llegó a usar números negativos ni a definir las curvas a partir de ecuaciones, sino que las ecuaciones venían después de las curvas.
Contribuciones de Persia
En el siglo XI, el matemático persa Omar Jayam vio una conexión muy fuerte entre la geometría y el álgebra. Él ayudó a unir estas dos ramas al resolver ecuaciones complejas usando métodos geométricos. Su trabajo fue muy importante y se considera que sentó las bases de la geometría algebraica, que luego llegó a Europa.
Desarrollo en Europa Occidental
La geometría analítica, tal como la conocemos, fue desarrollada de forma independiente por René Descartes y Pierre de Fermat en el siglo XVII. A menudo, se le da más crédito a Descartes, y por eso a veces se le llama "geometría cartesiana".
Descartes publicó sus ideas en un ensayo llamado La Géométrie en 1637, como parte de su famoso libro Discurso del método. Al principio, su trabajo fue un poco difícil de entender, pero después de que fue traducido al latín y explicado por otros matemáticos como Frans van Schooten, se hizo muy influyente.
Pierre de Fermat también hizo grandes avances. Él empezaba con una ecuación algebraica y luego describía la figura geométrica que le correspondía. Descartes, en cambio, partía de las figuras geométricas para encontrar sus ecuaciones. Esta diferencia hizo que Descartes tuviera que trabajar con ecuaciones más complejas. Más tarde, Leonhard Euler aplicó este método para estudiar superficies y curvas en el espacio.
Cómo Funciona la Geometría Analítica
En un sistema de coordenadas cartesianas, cada punto en un plano se describe con dos números: la abscisa (coordenada x) y la ordenada (coordenada y). Estos dos números forman un par ordenado 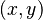 . De esta manera, cada punto tiene un par de números único, y cada par de números representa un punto único. Esta conexión entre puntos y números es la base de la geometría analítica.
. De esta manera, cada punto tiene un par de números único, y cada par de números representa un punto único. Esta conexión entre puntos y números es la base de la geometría analítica.
Con la geometría analítica, podemos describir figuras geométricas planas usando ecuaciones. Esto nos da una nueva forma de resolver problemas matemáticos.
Ubicación de un Punto en el Plano Cartesiano
Distancia a los Ejes
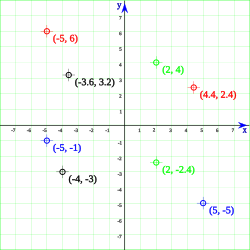
Imagina una hoja de papel milimetrado. Trazamos dos líneas que se cruzan formando un ángulo recto: una horizontal (el eje X) y una vertical (el eje Y). Cualquier punto en esta hoja se puede encontrar midiendo su distancia a cada uno de estos ejes.
El primer número del par 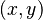 es la distancia al eje vertical (eje Y) y se llama abscisa. Si es positivo, la distancia se mide hacia la derecha; si es negativo, hacia la izquierda.
es la distancia al eje vertical (eje Y) y se llama abscisa. Si es positivo, la distancia se mide hacia la derecha; si es negativo, hacia la izquierda.
El segundo número es la distancia al eje horizontal (eje X) y se llama ordenada. Si es positivo, la distancia se mide hacia arriba; si es negativo, hacia abajo.
- Los puntos sobre el eje X tienen una ordenada de
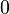 , por ejemplo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (5, 0) .
, por ejemplo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (5, 0) . - Los puntos sobre el eje Y tienen una abscisa de
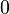 , por ejemplo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (0, 3) .
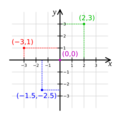
, por ejemplo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (0, 3) . - El punto donde los dos ejes se cruzan se llama origen de coordenadas y sus coordenadas son
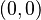 .
.
Proyección sobre los Ejes
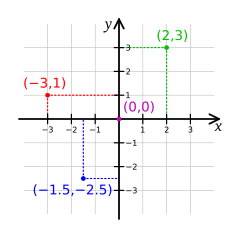
Otra forma de ver las coordenadas es como las "sombras" de un punto sobre los ejes. Si tienes un punto P, trazas una línea recta desde P que sea perpendicular al eje X. Donde esa línea cruza el eje X, tienes la coordenada x del punto. Haces lo mismo para el eje Y.
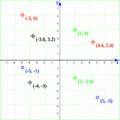
Por ejemplo:
- Si un punto P está 2 unidades a la derecha del origen en el eje X y 3 unidades hacia arriba en el eje Y, sus coordenadas son (2, 3).
- Si está 4 unidades a la derecha en X y 5 unidades hacia abajo en Y, sus coordenadas son (4, -5).
- Si está 3 unidades a la izquierda en X y 2 unidades hacia abajo en Y, sus coordenadas son (-3, -2).
- Si está 6 unidades a la izquierda en X y 4 unidades hacia arriba en Y, sus coordenadas son (-6, 4).
Ecuaciones de la Recta en el Plano
Una recta es una línea recta que se extiende infinitamente. En geometría analítica, una recta se puede describir con una ecuación.
La forma general de la ecuación de una recta es: 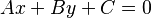
También se puede escribir como una función lineal:
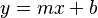
Aquí, m es la pendiente (qué tan inclinada está la recta) y b es el punto donde la recta cruza el eje Y.
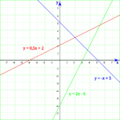
Hay tres tipos principales de rectas:
| Rectas oblicuas. | Rectas horizontales. | Rectas verticales. |
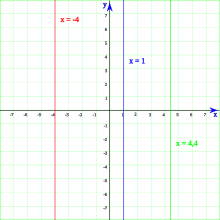
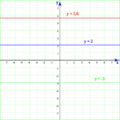
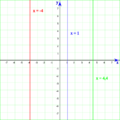
- Las rectas verticales son líneas rectas que van de arriba a abajo. No cruzan el eje Y. Su ecuación es
 , donde
, donde 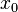 es el valor por donde pasa en el eje X.
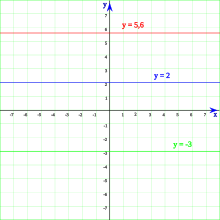
es el valor por donde pasa en el eje X. - Las rectas horizontales son líneas rectas que van de izquierda a derecha. No cruzan el eje X. Su ecuación es
 , donde
, donde 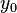 es el valor por donde pasa en el eje Y.
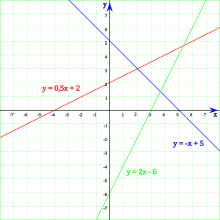
es el valor por donde pasa en el eje Y. - Cualquier otra recta se llama recta oblicua. Estas cruzan tanto el eje X como el eje Y.
Secciones Cónicas
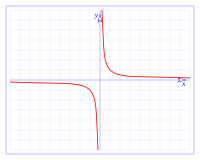
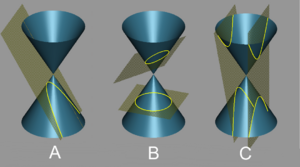
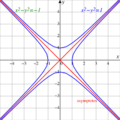
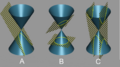
Las secciones cónicas son figuras que se forman cuando cortamos un cono con un plano. Las principales son la parábola, la elipse (donde la circunferencia es un caso especial) y la hipérbola.
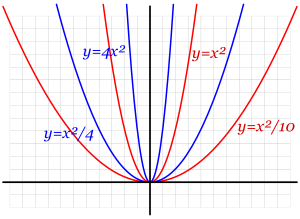
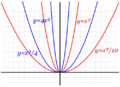
- La parábola (figura A) es la forma que toma el chorro de agua de una fuente o la trayectoria de una pelota lanzada. Se describe con ecuaciones como:
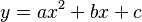
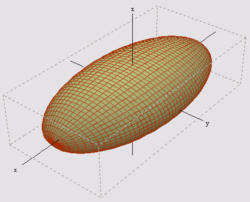
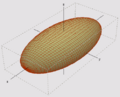
- La elipse (figura B) es como un círculo estirado. Las órbitas de los planetas alrededor del Sol son elipses. Su ecuación es:
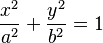
Si los valores a y b son iguales, la elipse se convierte en una circunferencia, con la ecuación:
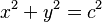
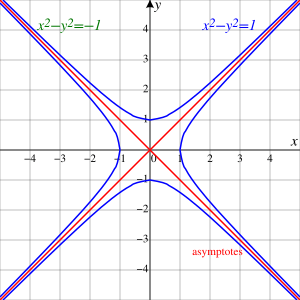
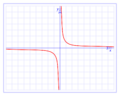
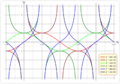
- La hipérbola (figura C) son dos curvas separadas que se abren en direcciones opuestas. Su ecuación es:
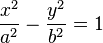
Expresión Algebraica de Cónicas
En coordenadas cartesianas, todas las cónicas se pueden describir con una ecuación general que tiene términos al cuadrado: 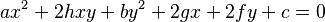 Dependiendo de los valores de las letras (a, h, b, g, f, c), la ecuación representará una hipérbola, parábola, elipse o circunferencia.
Dependiendo de los valores de las letras (a, h, b, g, f, c), la ecuación representará una hipérbola, parábola, elipse o circunferencia.
Funciones Trigonométricas
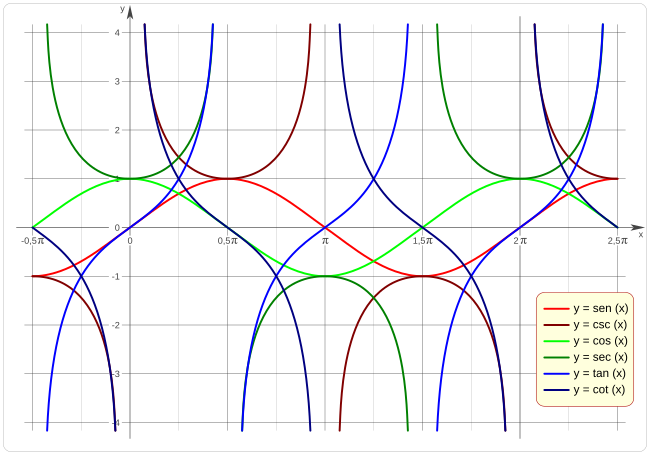
La geometría analítica también nos permite dibujar y estudiar las funciones trigonométricas (como seno, coseno, tangente) en un sistema de coordenadas. Estas funciones son muy útiles para describir ondas y movimientos repetitivos.
Construcciones en el Espacio Tridimensional
Así como podemos ubicar puntos en un plano con dos coordenadas (x, y), podemos ubicar puntos en el espacio tridimensional usando tres coordenadas (x, y, z). Para esto, se añade un tercer eje (el eje Z) que es perpendicular a los ejes X e Y.
En el espacio, una sola ecuación lineal como:

representa un plano. Para describir una recta en el espacio, necesitamos dos ecuaciones lineales, ya que una recta puede verse como la intersección de dos planos. Por ejemplo:
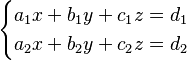
Importancia de la Geometría Analítica
La geometría analítica es un puente muy importante entre la geometría euclidiana (la geometría de las formas y espacios que estudiamos en la escuela) y otras ramas de las matemáticas, como el análisis matemático y el álgebra lineal.
En física, se usan los sistemas de coordenadas para representar el movimiento de los objetos, los vectores y otras cantidades. Esto demuestra lo útil que es la geometría analítica en el mundo real.
Galería de imágenes
Véase también
 En inglés: Analytic geometry Facts for Kids
En inglés: Analytic geometry Facts for Kids