Maple (software) para niños
Datos para niños Maple |
||
|---|---|---|
 |
||
| Información general | ||
| Tipo de programa | Software matemático | |
| Desarrollador | Maplesoft | |
| Lanzamiento inicial | 1982 | |
| Licencia | Propietario | |
| Idiomas | Inglés | |
| Información técnica | ||
| Programado en | C, Java, Maple | |
| Plataformas admitidas | x86, x86-64 | |
| Versiones | ||
| Última versión estable | 2019 (14 de marzo de 2019) | |
| Archivos legibles | ||
|
||
| Archivos editables | ||
|
||
| Enlaces | ||
|
Página pirncipal de Sitio web oficial
|
||
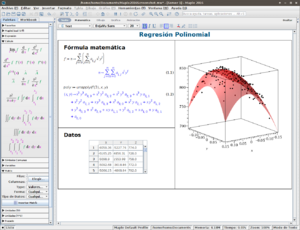
Maple es un programa de computadora muy útil para resolver problemas de matemáticas. Puede hacer cálculos complejos, trabajar con símbolos y resolver ecuaciones de álgebra. Es como una calculadora muy avanzada que también entiende el lenguaje de las matemáticas.
Fue creado en 1981 por un grupo de expertos en la Universidad de Waterloo en Waterloo, Ontario, Canadá. Desde 1988, una empresa canadiense llamada Maplesoft (antes Waterloo Maple Inc.) se encarga de mejorarlo y venderlo.
Maple funciona con un programa principal escrito en el lenguaje de programación C. La mayoría de sus funciones adicionales están hechas con el propio lenguaje de Maple. Este programa guarda las expresiones matemáticas como si fueran mapas especiales para procesarlas.
Contenido
¿De dónde viene el nombre Maple?
El nombre "Maple" tiene dos significados. Uno es que suena parecido a "Math Pleasure" (placer de las matemáticas) en inglés. El otro es un homenaje a Canadá, el país donde se creó. La bandera de Canadá tiene una hoja de arce, que en inglés se dice maple.
¿Qué puede hacer Maple?
Maple es una herramienta muy potente para estudiantes y profesionales. Aquí te contamos algunas de las cosas que puede hacer:
- Realizar cálculos matemáticos muy precisos, tanto con números como con símbolos.
- Resolver problemas de álgebra, como trabajar con polinomios.
- Calcular límites, series y sucesiones.
- Manejar números complejos y sus operaciones.
- Trabajar con matrices, que son tablas de números usadas en matemáticas.
- Crear gráficos y animaciones para visualizar funciones matemáticas.
- Resolver diferentes tipos de ecuaciones diferenciales, que describen cómo cambian las cosas.
- Hacer cálculos de cálculo, como integrales y derivadas.
- Ayudar con problemas de optimización, buscando la mejor solución posible.
- Ofrecer herramientas de estadística para analizar datos y hacer pruebas.
- Trabajar con probabilidad y series de tiempo.
- Conectarse a datos en línea para aplicaciones financieras.
- Realizar cálculos financieros, como los relacionados con bonos.
- Simular procesos aleatorios.
- Procesar texto y fórmulas matemáticas.
- Permite crear interfaces para desarrollar cálculos y aplicaciones.
- Puede conectarse con otros programas y lenguajes de programación como Java, C++ y Python.
Ejemplos de lo que Maple puede calcular
Maple puede resolver muchos tipos de problemas matemáticos. Aquí tienes algunos ejemplos sencillos:
Resolver ecuaciones
Maple puede encontrar las soluciones para ecuaciones. Por ejemplo, si le pides que resuelva una ecuación de segundo grado como 3x² + bx = 7, te dará las fórmulas para encontrar los valores de 'x'.
Calcular raíces cuadradas
Puedes pedirle a Maple que calcule la raíz cuadrada de un número con muchas cifras decimales. Por ejemplo, la raíz cuadrada de 2 es aproximadamente 1.41421356237309504880.
Simplificar fracciones
Si tienes una operación con fracciones, como 35/42 - 5/30, Maple puede simplificarla y darte el resultado más sencillo, que en este caso sería 2/3.
Encontrar derivadas e integrales
Maple es muy bueno para el cálculo. Puede encontrar la derivada de una función o calcular integrales, tanto de forma simbólica (con letras) como numérica (con números).
Versiones de Maple
Maplesoft ofrece versiones de Maple para profesionales y para estudiantes. Las versiones para estudiantes suelen ser más económicas.
Desde la versión 6, las versiones para estudiantes tienen casi todas las funciones de las versiones profesionales. La principal diferencia es que vienen con menos manuales impresos. Antes de la versión 6, las versiones para estudiantes tenían algunas limitaciones, como un máximo de 100 dígitos en los cálculos o un tamaño limitado para ciertos objetos matemáticos.
Comandos básicos en Maple
Maple entiende las funciones como "árboles de expresión". Esto significa que organiza las operaciones de una manera especial.
¿Cómo saber el tipo de una expresión?
Si quieres saber cómo Maple interpreta una función, puedes usar el comando `whattype()`. Por ejemplo, si defines `p:= x^2+4*x+4`, y luego escribes `whattype(p)`, Maple te dirá qué tipo de expresión es.
¿Cómo escribir una función?
Para definir una función en Maple, usas `:=`. Por ejemplo, para una función `p` igual a `x^2+4*x+4`, escribirías: `p:= x^2+4*x+4;`
Si quieres saber el valor de esa función cuando `x` es, por ejemplo, 3, primero asignas el valor a `x` y luego pides el valor de `p`: `x:= 3;` `p;` Si ya no quieres que `x` tenga ese valor, puedes "borrarlo" así: `x:= 'x';`
¿Cómo encontrar una integral?
Para encontrar la integral (o antiderivada) de una función, usas el comando `int()`. Si tienes `p:= x^2+4*x+4`, para encontrar su integral con respecto a `x`, escribirías: `int(p,x);` Maple te mostrará la antiderivada.
Historial de actualizaciones
Maple se actualiza con frecuencia para añadir nuevas funciones y mejorar las existentes. Algunas de las versiones más recientes incluyen:
- Maple 2020: marzo de 2020
- Maple 2019: marzo de 2019
- Maple 2018: marzo de 2018
- Maple 2017: mayo de 2017
- Maple 2016: marzo de 2016
- Maple 2015: marzo de 2015
- Maple 18: marzo de 2014
Galería de imágenes
Véase también
 En inglés: Maple (CAS) Facts for Kids
En inglés: Maple (CAS) Facts for Kids
- Lista de programas de álgebra computacional