Dilema del prisionero para niños
El dilema del prisionero es un problema muy interesante de la teoría de juegos. Muestra cómo dos personas, actuando cada una por su propio interés, pueden terminar con un resultado que no es el mejor para ninguna de ellas. Es como si, al intentar ganar individualmente, ambos perdieran una oportunidad de estar mejor juntos.
Este problema fue creado por Merrill M. Flood y Melvin Dresher en 1950. Más tarde, Albert W. Tucker le dio el nombre de "dilema del prisionero" y lo explicó con la historia de las recompensas en la cárcel.
Es un ejemplo de un problema donde lo que uno gana no es exactamente lo que el otro pierde (se llama "suma no nula"). Las herramientas de la teoría de juegos a veces sugieren que cada persona debería "traicionar" a la otra. Sin embargo, si ambos hubieran cooperado, el resultado para los dos habría sido mucho mejor.
Cuando el dilema del prisionero se juega muchas veces (se llama dilema del prisionero iterado), la cooperación puede aparecer. Esto ocurre porque los jugadores tienen la oportunidad de "castigar" al otro si no cooperó en las rondas anteriores. Así, la amenaza de un castigo futuro puede hacer que la gente decida cooperar.
Contenido
¿Qué es el dilema del prisionero clásico?
Imagina esta situación:
La policía detiene a dos sospechosos de un delito. No tienen pruebas suficientes para condenarlos a una pena grande. Los separan y les ofrecen el mismo trato a cada uno:
- Si uno confiesa y el otro no, el que confesó queda libre. El que no confesó recibe una pena de diez años.
- Si ambos confiesan, los dos reciben una pena de seis años.
- Si ambos se quedan callados y no confiesan, solo pueden encerrarlos por un delito menor, y cada uno recibe una pena de un año.
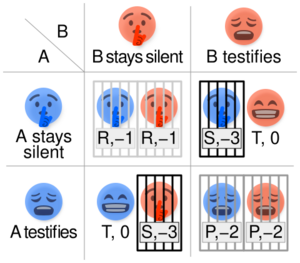
Aquí tienes un resumen de las opciones y sus resultados:
| Tú confiesas | Tú te callas | |
|---|---|---|
| Él confiesa | Ambos reciben 6 años. | Tú recibes 10 años y él queda libre. |
| Él se calla | Él recibe 10 años y tú quedas libre. | Ambos reciben 1 año. |
Supongamos que los dos sospechosos solo piensan en sí mismos y quieren pasar el menor tiempo posible en la cárcel. Cada uno tiene dos opciones: cooperar con el otro (quedarse callado) o traicionar al otro (confesar). El resultado de su elección depende de lo que haga el otro. El problema es que no saben qué elegirá el otro. Incluso si pudieran hablar, no podrían estar seguros de que el otro cumpliría su palabra.
Si uno de los sospechosos piensa que el otro se quedará callado, lo mejor para él sería confesar. Así, saldría libre de inmediato, mientras el otro pasaría diez años en la cárcel. Si piensa que el otro va a confesar, lo mejor para él también sería confesar. De esa forma, solo pasaría seis años en la cárcel, en lugar de los diez si se quedara callado.
Pero, ¡aquí está la clave del dilema! Si ambos decidieran cooperar y quedarse callados, ¡ambos saldrían en solo un año!
Confesar es la "mejor" opción para cada sospechoso individualmente, sin importar lo que haga el otro. Esto se llama una estrategia dominante. Sin embargo, esta elección individual lleva a que ambos confiesen y reciban una pena de seis años. Este resultado no es el mejor para el grupo, porque si hubieran cooperado, ambos habrían recibido solo un año.
Si se piensa en el beneficio de los dos sospechosos juntos, lo mejor sería que ambos se quedaran callados. Esto reduciría el tiempo total de cárcel a solo dos años (uno para cada uno). Pero si cada uno actúa solo por su propio interés, terminan con una pena más larga.
¿Cómo se ve el dilema en números?
En el dilema del prisionero, los resultados se pueden representar con números. Imagina que los años de cárcel son números negativos (porque son algo malo).
- T (Tentación): Lo que ganas si traicionas y el otro coopera (0 años para ti).
- R (Recompensa): Lo que ganas si ambos cooperan (1 año para ti, -1).
- C (Castigo): Lo que ganas si ambos traicionan (6 años para ti, -6).
- P (Paga del primo): Lo que ganas si tú cooperas y el otro traiciona (10 años para ti, -10).
La regla es que siempre se cumple: T > R > C > P. En nuestro ejemplo de la cárcel, esto sería: 0 > -1 > -6 > -10. Esto significa que siempre es mejor para cada persona traicionar, sin importar lo que haga el otro.
A veces, para simplificar, se usan números positivos para representar "ganancias" en lugar de "pérdidas" (años de cárcel). Por ejemplo:
| Cooperar | Traicionar | |
|---|---|---|
| Cooperar | 3, 3 | -5, 5 |
| Traicionar | 5, -5 | -1, -1 |
Aquí, el primer número es tu ganancia y el segundo es la del otro. Si ambos cooperan, ambos ganan 3. Si tú traicionas y el otro coopera, tú ganas 5 y él pierde 5.
Interés propio vs. bien común
El dilema del prisionero nos hace pensar en la diferencia entre lo que es mejor para una persona individualmente y lo que es mejor para un grupo.
Mira esta tabla que muestra los años de cárcel para cada uno y el total:
| Sospechoso A | Sospechoso B | Sospechoso A (años) | Sospechoso B (años) | Total (años) |
|---|---|---|---|---|
| Se calla | Se calla | 1 | 1 | 2 |
| Se calla | Confiesa | 10 | 0 | 10 |
| Confiesa | Se calla | 0 | 10 | 10 |
| Confiesa | Confiesa | 6 | 6 | 12 |
Si miramos el "Total (años)", la mejor decisión para ambos juntos es "Se calla" y "Se calla", porque el total de años en la cárcel es solo 2. Sin embargo, si cada uno piensa solo en sí mismo, la decisión de "Confesar" parece la mejor para cada uno, lo que lleva a un total de 12 años.
Esto nos enseña que a veces, para lograr el mejor resultado para uno mismo a largo plazo, es necesario pensar en el bien de todos. El altruismo (pensar en los demás) puede llevar a mejores resultados para todos, incluso para uno mismo.
Ejemplos en la vida diaria
Aunque el ejemplo de los prisioneros parece de película, el dilema del prisionero se ve en muchas situaciones de la vida real. Por eso es importante para ciencias como la economía, la política y la biología.
La carrera de armamentos
Imagina dos países que tienen miedo el uno del otro. Ambos pueden elegir aumentar su armamento o hacer un acuerdo para reducirlo. Ninguno puede estar seguro de que el otro cumplirá el acuerdo. Por lo tanto, ambos tienden a aumentar sus armas. La ironía es que, aunque cada país actúa de forma "racional" para protegerse, el resultado final es que ambos gastan mucho dinero en armas y están menos seguros.
Ciclistas en una carrera
En una carrera de ciclismo, dos ciclistas que van escapados pueden trabajar juntos (cooperar) turnándose para ir delante y cortar el viento. Si ninguno de los dos hace el esfuerzo, el grupo principal los alcanzará rápido (ambos pierden). A veces, uno hace todo el trabajo (coopera) y el otro se queda detrás (traiciona). Al final, el que se quedó detrás puede tener más energía y ganar la carrera.
Cruces de calles
En un cruce sin semáforos, si todos los conductores se turnan para pasar (cooperan), el tráfico fluye bien. Si alguien no coopera y trata de pasar primero, causa un desorden que perjudica a todos. Si nadie coopera y todos intentan pasar a la vez, se forma un gran atasco donde todos pierden mucho tiempo.
El dilema del prisionero iterado
Robert Axelrod estudió qué pasa cuando el dilema del prisionero se juega muchas veces seguidas. A esto lo llamó el dilema del prisionero iterado (DPI). En este caso, los jugadores recuerdan lo que pasó en las rondas anteriores.
Axelrod hizo un concurso donde invitó a expertos a crear programas de computadora para jugar al DPI. Descubrió que las estrategias que eran "egoístas" (siempre traicionar) no funcionaban tan bien a largo plazo. En cambio, las estrategias más "altruistas" (que cooperaban) obtenían mejores resultados. Esto ayudó a entender cómo la cooperación puede surgir incluso en situaciones donde la gente busca su propio beneficio.
La mejor estrategia que se encontró fue "Toma y daca" (tit for tat). Esta estrategia es muy simple:
- En la primera ronda, coopera.
- Después, haz lo mismo que hizo tu oponente en la ronda anterior. Si cooperó, coopera. Si traicionó, traiciona.
"Toma y daca" funciona porque es "amable" (empieza cooperando) y también es "firme" (castiga la traición inmediatamente). Esto hace que el otro jugador entienda rápidamente cómo funciona y pueda aprender a cooperar.
Una versión un poco mejor es "Toma y daca con capacidad de perdón". A veces, si el otro jugador traiciona, esta estrategia coopera de nuevo con una pequeña probabilidad. Esto ayuda a evitar que los jugadores se queden atrapados en un ciclo de traiciones mutuas.
En el DPI, si los jugadores saben exactamente cuántas rondas se van a jugar, la mejor estrategia es traicionar siempre. Esto es porque en la última ronda, no hay castigo futuro, así que ambos traicionarán. Y si saben que en la última ronda traicionarán, entonces en la penúltima también, y así sucesivamente. Para que la cooperación funcione, el futuro debe ser incierto.
Este juego es muy importante para entender cómo las personas cooperan y confían entre sí.
Sociedades secretas en el dilema del prisionero iterado
En un torneo del dilema del prisionero iterado en 2004, un equipo de la Universidad de Southampton ganó usando una estrategia muy astuta. Presentaron muchos programas que eran variantes del mismo algoritmo. Al principio del juego, estos programas usaban sus primeras jugadas como un "saludo secreto" para identificarse entre sí.
Si un programa de Southampton identificaba a otro como parte de su "sociedad", algunos de ellos se "sacrificaban" cooperando siempre. Esto permitía que los otros programas de la "sociedad" los traicionaran siempre y obtuvieran la máxima puntuación. Si no identificaban al otro jugador como parte de su grupo, todos los programas de Southampton lo traicionaban siempre para bajar su puntuación.
Esta estrategia, aunque un poco tramposa, les permitió ganar los primeros puestos, a costa de que muchos de sus propios programas quedaran en los últimos lugares.
Otras versiones del dilema
Existen otras situaciones parecidas al dilema del prisionero, con pequeñas diferencias:
El juego de la gallina
En este juego, si tu oponente traiciona, a ti te conviene cooperar. El peor resultado es que ambos traicionen. Se llama "gallina" por el juego de coches donde dos conductores van uno hacia el otro y el primero en desviarse es el "gallina". Si ambos se desvían (cooperan), evitan el choque. Si ninguno se desvía (traicionan), chocan.
El juego de confianza
Aquí, un jugador decide cuánto confía en el otro. Cuanta más confianza, más dinero se genera para el segundo jugador. Luego, el segundo jugador decide cuánto devolver al primero. Si se juega una sola vez, el segundo jugador podría quedarse con todo. Pero si se juega repetidamente, la confianza y la cooperación pueden llevar a que ambos ganen mucho más.
Amigo o enemigo
Este es un juego de televisión. Dos personas compiten y, al final, juegan una ronda del dilema del prisionero para repartir sus ganancias.
- Si ambos eligen "amigo" (cooperan), comparten el dinero 50/50.
- Si uno elige "amigo" y el otro "enemigo" (traiciona), el "enemigo" se lleva todo y el "amigo" nada.
- Si ambos eligen "enemigo", ninguno se lleva nada.
Este juego es interesante porque solo se juega una vez, así que no hay oportunidad de "castigar" al otro en futuras rondas.
La "tragedia de los comunes"
Este es un dilema del prisionero que involucra a muchas personas. Imagina un pasto que es de todos en un pueblo. Cada granjero quiere que su ganado coma allí porque es el mejor. Si muchos granjeros hacen esto sin control, el pasto se agota y nadie puede usarlo.
Esto se aplica a muchos recursos compartidos, como el medio ambiente. Si todos contaminan sin preocuparse, el aire y el agua se dañan, y todos sufren las consecuencias. Para evitar esto, a veces se necesita que la gente coopere y piense en el bien común, incluso si eso significa un pequeño sacrificio individual.
Galería de imágenes
Véase también
 En inglés: Prisoner's dilemma Facts for Kids
En inglés: Prisoner's dilemma Facts for Kids