Efecto Compton para niños
El efecto Compton (también conocido como dispersión Compton) es un fenómeno que ocurre cuando un fotón (una partícula de luz) choca con un electrón libre. Después de la colisión, el fotón pierde parte de su energía y, como resultado, su longitud de onda se hace más larga. La cantidad en que cambia la longitud de onda del fotón depende del ángulo en que se dispersa (es decir, la dirección en que sale después del choque).
Este efecto es muy importante porque demuestra que la luz no solo se comporta como una onda, sino también como una partícula.
Contenido
¿Quién descubrió el efecto Compton?
El efecto Compton fue estudiado por el físico Arthur Compton en 1923. Él logró explicar este fenómeno usando ideas de la mecánica cuántica, que describe cómo se comporta la energía en el mundo muy pequeño de los átomos y las partículas. También usó la teoría de la relatividad de Albert Einstein.
¿Cómo se descubrió el efecto Compton?
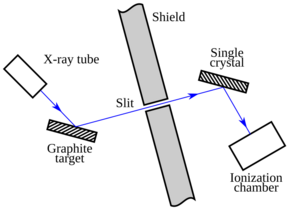
Compton descubrió este efecto mientras experimentaba con rayos X. Dirigió estos rayos hacia un bloque de carbón. Al chocar, los rayos X se dispersaron en diferentes direcciones. Compton notó que cuanto mayor era el ángulo de dispersión de los rayos, más larga se volvía su longitud de onda.
Explicó que esto sucedía porque el fotón de rayos X actuaba como una pequeña partícula al chocar con el electrón. Al hacerlo, le transfería parte de su energía al electrón, lo que hacía que el fotón perdiera energía y cambiara su longitud de onda.
Gracias a este importante descubrimiento, Arthur Compton recibió el Premio Nobel de Física en 1927.
¿Por qué es importante el efecto Compton?
El efecto Compton fue una prueba clave de que la luz tiene una doble naturaleza: puede comportarse como una onda y como una partícula. Antes de Compton, otros científicos como Max Planck y Albert Einstein ya habían sugerido que la luz tenía propiedades de partícula, pero el efecto Compton fue la demostración final.
Esta idea de que la luz es tanto onda como partícula es fundamental en la mecánica cuántica.
¿Cómo funciona la dispersión Compton?
Imagina que un fotón de luz choca con un electrón que está casi libre. El fotón le da parte de su energía al electrón, lo que hace que el electrón se mueva (o "retroceda"). El fotón, con menos energía, se desvía y sale en una dirección diferente a la original.
Este proceso es como una colisión entre dos bolas de billar: la energía y el movimiento total se conservan. Si el fotón dispersado todavía tiene suficiente energía, podría chocar con otro electrón y repetir el proceso.
Aplicaciones del efecto Compton
El efecto Compton es muy importante en varias áreas de la ciencia y la tecnología:
- Medicina: Es crucial en la radiobiología y la radioterapia. Cuando los rayos gamma y los rayos X de alta energía interactúan con los tejidos del cuerpo, la dispersión Compton es la interacción más común. Esto ayuda a entender cómo la radiación afecta a los seres vivos y cómo usarla para tratar enfermedades.
- Astronomía: En la astrofísica, existe un fenómeno llamado dispersión Compton inversa. Esto ocurre cuando fotones de baja energía (como los de la radiación cósmica de fondo de microondas) chocan con electrones muy energéticos. Los fotones ganan energía y se vuelven más energéticos. Esto se observa, por ejemplo, en los cúmulo de galaxias y ayuda a los científicos a estudiar estos objetos gigantes en el universo.
- Física nuclear: Algunas instalaciones usan la dispersión Compton inversa para producir fotones de muy alta energía, que luego se utilizan en experimentos de física nuclear.
Galería de imágenes
-
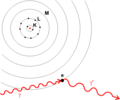
Representación gráfica de la dispersión de un fotón γ (línea roja ondulada), por un electrón. El fotón dispersado tiene una longitud de onda mayor (o una frecuencia menor) que antes de interactuar con el electrón.