Espín para niños
El espín (del inglés spin, que significa 'giro') es una característica especial de las partículas elementales, como los electrones. Imagina que las partículas tienen un "giro" interno, aunque no es un giro como el de una peonza. Este giro les da una especie de momento angular propio, que es una medida de la cantidad de movimiento de rotación.
El concepto de espín fue propuesto en 1925 por científicos como Ralph Kronig, George Uhlenbeck y Samuel Goudsmit. Además del espín, otra característica importante de las partículas elementales es su carga eléctrica.
Contenido
¿Qué es el Espín y Por Qué es Importante?
Descubrimiento del Espín
Hace tiempo, los científicos se dieron cuenta de que la teoría cuántica no podía explicar completamente algunas propiedades de la luz que emiten los átomos (llamados espectros atómicos). Los físicos Goudsmit y Uhlenbeck descubrieron que si añadían un número especial, llamado "número cuántico de espín", podían entender mejor estos espectros.
La primera vez que se vio una prueba de la existencia del espín fue en 1922, con un experimento famoso de Otto Stern y Walther Gerlach. Aunque no entendieron completamente lo que veían hasta 1927, este experimento fue clave. Poco después, se dieron cuenta de que el espín no solo existía en los electrones, sino también en otras partículas muy pequeñas, como los protones, los neutrones y las antipartículas.
¿Cómo se Relaciona el Espín con el Giro?
El espín nos dice cuánto "momento angular" tiene una partícula por sí misma. En el mundo que vemos todos los días (la mecánica clásica), el momento angular se relaciona con el giro de un objeto grande, como una pelota que gira. Pero el espín es diferente; es un fenómeno que solo existe en el mundo de lo muy pequeño, el mundo cuántico.
No podemos imaginar el espín como una partícula girando sobre su propio eje como una peonza. Es más bien una propiedad fundamental que siempre está ahí. No importa cómo lo midas, siempre encontrarás que la partícula tiene este momento angular interno.
Existe una conexión muy interesante entre el espín de una partícula y cómo se comportan muchas partículas iguales juntas. Esta relación se ha observado y se puede demostrar con teorías avanzadas de la física.
Propiedades Clave del Espín
El espín tiene algunas características especiales que lo hacen diferente del momento angular que conocemos en el mundo grande:
- Valores Fijos: El espín no puede tener cualquier valor. Solo puede tomar ciertos valores específicos, como si fueran escalones en una escalera.
- Múltiplos de una Constante: El valor del espín de una partícula siempre es un múltiplo de la mitad de una constante muy pequeña llamada "constante reducida de Planck" (que se escribe
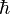). - Proyecciones Específicas: Cuando medimos el espín en una dirección particular, solo obtenemos algunos valores posibles. Por ejemplo, el espín de un electrón, si se mide en una dirección específica (como la de un campo magnético), solo puede ser
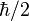o 
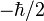. - Magnitud Única: Cada tipo de partícula elemental tiene una magnitud total de espín que es única para ella. Por ejemplo, los electrones, protones y neutrones siempre tienen la misma magnitud de espín. Esto es diferente de un objeto grande, que puede girar más rápido o más lento.
Espín y la Clasificación de Partículas
Existe una propiedad fundamental que clasifica a las partículas cuánticas en dos grandes grupos: los fermiones y los bosones. Los fermiones siguen unas reglas estadísticas llamadas "estadística de Fermi-Dirac", y los bosones siguen las "estadísticas de Bose-Einstein".
Lo interesante es que hay una conexión directa entre el tipo de partícula y su espín:
- Los fermiones tienen espines que son múltiplos de la mitad de la constante 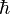(como 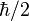, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3\hbar/2 , etc.).
- Los bosones tienen espines que son múltiplos enteros de la constante 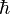(como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0\hbar , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1\hbar ,
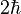, etc.).
Por ejemplo, los electrones, neutrones y protones son fermiones con espín 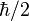. Los fotones (las partículas de luz) son bosones con espín 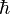. Algunas partículas, como el pion o el bosón de Higgs, tienen espín cero.
Espín y el Magnetismo
Las partículas con espín tienen algo llamado "momento magnético". Esto es un poco como si fueran pequeños imanes. Al principio, se pensó que esto se debía a que la partícula cargada estaba girando, como un pequeño planeta cargado. Sin embargo, esta idea no es del todo correcta, porque incluso partículas sin carga, como el fotón, tienen espín y un momento magnético.
El ferromagnetismo, que es lo que hace que algunos materiales sean imanes permanentes (como los imanes de nevera), ocurre porque los espines de muchas partículas en el material se alinean en la misma dirección.
Espín y la Luz (Polarización)
El espín de un fotón (la partícula de luz) es lo que describe la polarización de la luz. La polarización es la dirección en la que vibran las ondas de luz. Cuando la luz tiene una polarización circular definida, significa que está hecha de fotones que tienen el mismo espín, ya sea +1 o -1, lo que indica la dirección de su giro.
Aplicaciones del Espín en la Tecnología
Discos Duros y Láseres
Hoy en día, la tecnología ya usa algunas propiedades del espín. Un ejemplo es la magnetorresistencia, que se utiliza en los discos duros de las computadoras para leer y escribir información.
Otro ejemplo son los láseres. Los láseres funcionan porque los fotones, que son bosones (partículas con espín entero), pueden ser forzados a estar todos en el mismo estado cuántico. Esto hace que produzcan una luz muy especial, con ondas que están perfectamente sincronizadas.
Espintrónica y Computación Cuántica
El estudio y uso de las propiedades del espín para crear nuevas tecnologías se llama espintrónica. Esta área busca ir más allá de la electrónica actual, manipulando espines individuales para mejorar la forma en que almacenamos y procesamos información.
También se está investigando cómo usar el espín para las futuras computadoras cuánticas. En estas computadoras, el espín de una partícula aislada podría servir como un "qubit" o bit cuántico. Un qubit es como un bit normal (que puede ser 0 o 1), pero con la capacidad de ser 0, 1 o una combinación de ambos al mismo tiempo. Esto podría hacer que las computadoras cuánticas sean mucho más potentes que las actuales, que se basan en el silicio.
Véase también
En inglés: Spin (physics) Facts for Kids
