Esfera para niños
En geometría, una superficie esférica es como la cáscara de una pelota. Imagina todos los puntos en el espacio que están a la misma distancia de un punto central. Ese punto central se llama centro, y la distancia se llama radio.
Si consideramos todos los puntos que están dentro de esa cáscara (es decir, a una distancia menor que el radio), junto con la cáscara misma, formamos lo que en matemáticas se llama una bola cerrada. En la geometría que aprendemos en la escuela, a esto lo llamamos simplemente esfera. Una esfera es un cuerpo geométrico, como una pelota o un globo terráqueo.
La palabra "esfera" viene del griego sphaîra, que significa "pelota para jugar". Coloquialmente, a menudo usamos la palabra "bola" para referirnos a este cuerpo.
Contenido
¿Qué es la esfera en geometría?
La esfera como superficie
La esfera, también conocida como superficie esférica, es el conjunto de todos los puntos en el espacio tridimensional que están a la misma distancia de un punto fijo llamado centro. La línea que une cualquier punto de la superficie con el centro, y la medida de esa línea, se llama radio. Puedes imaginarla como la superficie de una burbuja de jabón. Se forma al girar una semicircunferencia (la mitad de un círculo) alrededor de su diámetro.
La esfera como sólido
La esfera, o sólido esférico, incluye todos los puntos en el espacio tridimensional que están a una distancia igual o menor que el radio desde el centro. Piensa en una canica o una bola de billar. Se forma al girar un semicírculo (la mitad de un disco) alrededor de su diámetro.
Dentro de una esfera sólida, podemos distinguir:
- La frontera: Son los puntos que están exactamente a la distancia del radio del centro (la superficie esférica).
- El interior: Son los puntos que están a una distancia menor que el radio del centro.
- El exterior: Son los puntos que están a una distancia mayor que el radio del centro.
Estos tres grupos de puntos son distintos y juntos forman todo el espacio.
Propiedades importantes de la esfera
- Cualquier línea recta que pasa por el centro de la esfera y tiene sus extremos en la superficie se llama diámetro.
- Si cortas una esfera con un plano, la forma que obtienes siempre es un círculo.
- Si el corte pasa por el centro de la esfera, el círculo resultante se llama círculo mayor (como el ecuador de la Tierra). Si el corte no pasa por el centro, es un círculo menor.
- Los puntos en la superficie de la esfera que están más lejos de un círculo dado (y en la línea perpendicular a su centro) se llaman polos de ese círculo.
¿Cómo se calcula el volumen y el área de una esfera?
Volumen de una esfera
El volumen, que es la cantidad de espacio que ocupa una esfera, se calcula con la siguiente fórmula, usando su radio (r):
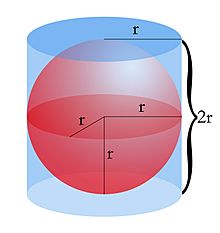
Un dato curioso es que el volumen de una esfera es dos tercios del volumen de un cilindro que la envuelve perfectamente (que tiene el mismo diámetro y altura que la esfera). Esta relación fue descubierta por el famoso matemático Arquímedes.
Área de la superficie de una esfera
El área de la superficie de una esfera se calcula multiplicando 4 por el valor de π y por el radio al cuadrado:
Arquímedes también demostró esta fórmula. Además, el área de la esfera es igual a la derivada de su volumen con respecto al radio, lo que es una forma avanzada de ver cómo cambian las cosas en matemáticas.
Ecuaciones de la esfera
Ecuación cartesiana
En un sistema de coordenadas (como un mapa en 3D con ejes X, Y, Z), la ecuación de una esfera con centro en el origen (0,0,0) y radio 1 es:
Si la esfera tiene un radio 'r' y su centro está en un punto (a, b, c), la ecuación general es:
Estas ecuaciones nos permiten describir la posición de cada punto en la superficie de la esfera.
Ecuaciones paramétricas
También podemos describir los puntos de una esfera usando ángulos, como si fueran coordenadas geográficas. Para una esfera con centro en (x0, y0, z0) y radio 'r', los puntos se pueden describir así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, x = x_0 + r \cos \theta \; \sen \varphi
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, y = y_0 + r \sen \theta \; \sen \varphi \qquad (0 \leq \theta \leq 2\pi \mbox{ , } 0 \leq \varphi \leq \pi ) \,

Aquí, θ y φ son los ángulos que nos ayudan a ubicar el punto en la superficie.
Secciones de una esfera

Cuando un plano corta una esfera, la forma que se crea en la intersección es siempre un círculo. La esfera es el único cuerpo geométrico que tiene esta propiedad. Si el plano solo toca la esfera en un punto, se considera un caso especial donde el círculo tiene radio cero.
Si el plano pasa justo por el centro de la esfera, el círculo que se forma tiene el mismo radio que la esfera. Este círculo se llama ecuador o círculo máximo.
Si el plano no pasa por el centro, el radio del círculo que se forma será más pequeño que el radio de la esfera. Podemos calcularlo usando el teorema de Pitágoras.
Dos esferas pueden cruzarse si la distancia entre sus centros es menor o igual a la suma de sus radios, y mayor o igual a la diferencia de sus radios. Si se cruzan, su intersección también es un círculo.
Planos especiales en la superficie esférica
Plano tangente
Un plano tangente es un plano que toca la esfera en un solo punto. Imagina que apoyas una hoja de papel sobre una pelota; esa hoja sería un plano tangente. Cada punto de la esfera tiene su propio plano tangente.
Coordenadas sobre la esfera
Para encontrar un punto en la superficie de una esfera, las coordenadas cartesianas (x, y, z) no son las más prácticas. Es mejor usar ángulos, como hacemos para ubicar lugares en la Tierra.
Podemos usar dos ángulos para localizar cualquier punto en la superficie de una esfera:
- Un ángulo horizontal (como la longitud en un mapa).
- Un ángulo vertical (como la latitud en un mapa).
En geografía, usamos grados para estos ángulos (latitud y longitud), tomando como referencia el meridiano de Greenwich y el polo norte. En geometría, a menudo se usan radianes porque facilitan otros cálculos.
Si añadimos un tercer valor, el radio 'r', podemos ubicar cualquier punto en el espacio usando las coordenadas esféricas (r, φ, θ).
Esferas en física


La esfera es una forma muy común en la naturaleza. ¿Sabías que, para un mismo volumen, la esfera tiene la superficie externa más pequeña? Esta propiedad es la razón por la que muchas cosas en el mundo físico tienen forma esférica. Por ejemplo, las gotas de agua o las burbujas de jabón son esféricas porque las fuerzas en su superficie hacen que tomen la forma que requiere la menor energía, y esa forma es la esfera.
Galería de imágenes
-
Proyección en dos dimensiones de una esfera definida mediante paralelos y meridianos.
Véase también
 En inglés: Sphere Facts for Kids
En inglés: Sphere Facts for Kids