Empaquetamiento de esferas para niños

En matemáticas, los problemas de empaquetamiento de esferas tratan sobre cómo organizar esferas del mismo tamaño para llenar un espacio de la manera más eficiente posible. Generalmente, este espacio es el que conocemos en nuestra vida diaria, el espacio tridimensional. Sin embargo, este desafío también se puede aplicar a dos dimensiones (donde las esferas son círculos), a espacios con más dimensiones (donde se llaman hiperesferas) o a otros tipos de espacios, como el espacio hiperbólico.
Un objetivo común en el empaquetamiento es encontrar la forma de colocar las esferas para que ocupen la mayor parte del espacio. A la cantidad de espacio que las esferas logran llenar se le llama densidad de empaquetamiento. Como esta densidad puede variar según cómo se mida, el problema busca la densidad promedio más alta en un espacio muy grande.
Existen dos tipos principales de empaquetamiento:
- Empaquetamiento regular o periódico: Las esferas forman un patrón muy simétrico que se repite.
- Empaquetamiento irregular o aperiódico: Las esferas no siguen un patrón simétrico.
Los patrones regulares son más fáciles de estudiar, clasificar y medir su densidad que los irregulares.
Contenido
Empaquetamiento de Círculos: ¿Cómo se Organizan en 2D?
En un espacio plano (dos dimensiones), el famoso matemático Carl Friedrich Gauss demostró que la forma más densa de organizar círculos de manera regular es el empaquetamiento hexagonal. En este arreglo, los centros de los círculos forman un patrón similar a un panal de abejas, y cada círculo está rodeado por otros seis. La densidad de este empaquetamiento es de aproximadamente 90.69%.
Más tarde, en 1940, el matemático húngaro László Fejes Tóth probó que el empaquetamiento hexagonal es el más denso de todos los empaquetamientos de círculos, ya sean regulares o irregulares.
Es importante saber que la rama de las matemáticas llamada "empaquetamiento de círculos" también estudia cómo organizar círculos de diferentes tamaños, lo que es un tema más complejo.
Empaquetamiento de Esferas: ¿Cuál es la Mejor Forma en 3D?
Empaquetamiento Periódico: Patrones Repetitivos
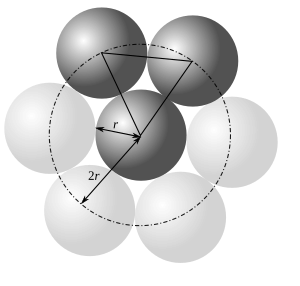
Imagina que tienes una capa de esferas muy bien organizadas en un plano. Si colocas una segunda capa encima, las nuevas esferas pueden caer en los huecos que dejan las esferas de abajo. Luego, una tercera capa puede colocarse de dos maneras diferentes: justo encima de la primera capa, o en los huecos que no fueron usados por la segunda capa. Esto crea diferentes tipos de capas, que se pueden llamar A, B y C.
Gauss demostró que estas formas de organizar las esferas en capas tienen la densidad más alta entre todos los arreglos regulares.
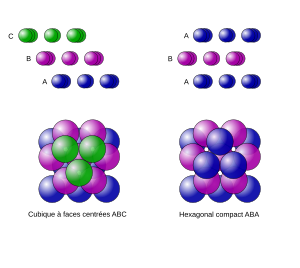
Las dos formas más comunes de empaquetamiento periódico son:
- Empaquetamiento cúbico centrado en caras: Las capas se alternan en un patrón ABCABC...
- Empaquetamiento hexagonal: Las capas se alternan en un patrón ABAB...
En ambos casos, cada esfera está rodeada por otras 12 esferas, y la densidad promedio es de aproximadamente 74.05%.
En 1611, el astrónomo Johannes Kepler propuso una idea, conocida como la conjetura de Kepler, que decía que esta densidad (74.05%) es la máxima posible para cualquier tipo de empaquetamiento de esferas, ya sea regular o irregular. No fue hasta 1998 que Thomas Hales, usando ideas de László Fejes Tóth y con la ayuda de computadoras, anunció que había confirmado la conjetura de Kepler. Su prueba fue muy compleja y revisó muchísimos casos individuales.
Empaquetamiento Aperiodico: Arreglos Irregulares
Cuando se colocan esferas al azar en un recipiente y luego se compactan, a menudo forman un empaquetamiento "irregular" o "atascado". Esto significa que no se pueden comprimir más. Este tipo de empaquetamiento irregular suele tener una densidad de alrededor del 64%.
Esta situación es diferente en una o dos dimensiones. Si compactas segmentos de línea (en 1D) o discos (en 2D) que se colocaron al azar, siempre terminarán formando un empaquetamiento regular.
Empaquetamiento de Hiperesferas: Más Allá de 3D
En dimensiones superiores a tres, el estudio del empaquetamiento de hiperesferas se vuelve más complejo. Se sabe que existen empaquetamientos regulares muy densos hasta en 8 dimensiones. Sin embargo, se sabe muy poco sobre los empaquetamientos irregulares en estas dimensiones. Es posible que, en algunas dimensiones, la forma más densa de empaquetamiento sea irregular. Por ejemplo, en 10 dimensiones, el empaquetamiento irregular más denso conocido es mejor que el regular.
La dimensión 24 es especial debido a la existencia de la red de Leech, que tiene el mayor número de esferas que pueden tocar a una esfera central (conocido como número de osculación). Durante mucho tiempo se pensó que esta red era el empaquetamiento más denso en esa dimensión. En 2004, los matemáticos Cohn y Kumar publicaron un estudio que apoyaba esta idea.
Espacio Hiperbólico: Un Desafío Diferente
Aunque los conceptos de círculos y esferas se pueden aplicar a los espacios hiperbólicos, encontrar el empaquetamiento más denso allí es mucho más difícil. En un espacio hiperbólico, no hay límite para la cantidad de esferas que pueden rodear a otra esfera. Además, el concepto de densidad promedio es más complicado de definir con precisión.
A pesar de estas dificultades, Charles Radin y Lewis Bowen, de la Universidad de Texas en Austin, demostraron en 2002 que el empaquetamiento más denso en casi cualquier espacio hiperbólico es generalmente irregular.
Otros Espacios y Aplicaciones
El estudio del empaquetamiento de esferas también tiene conexiones interesantes con otras áreas de las matemáticas y la tecnología. Por ejemplo, el empaquetamiento de esferas en las "esquinas" de un hipercubo (usando una medida llamada distancia de Hamming) está relacionado con la creación de códigos que corrigen errores en la transmisión de información. Si las esferas tienen un cierto "radio", sus centros pueden ser las claves de un código que corrige errores.
Véase también
 En inglés: Sphere packing Facts for Kids
En inglés: Sphere packing Facts for Kids
- Número de osculación
- Conjetura de Kepler
- Estructura de Weaire-Phelan
- Empaquetamiento de círculos