robot de la enciclopedia para niños

Métrica de Schwarzschild para niños

Enciclopedia para niños
Archivo:Flamm
Una representación del paraboloide de Flamm, que muestra cómo la gravedad curva el espacio alrededor de una estrella.

La métrica de Schwarzschild es una forma especial de describir cómo la gravedad de un objeto muy masivo, como una estrella o un planeta, afecta el espacio y el tiempo a su alrededor. Es una solución exacta de las ecuaciones de Albert Einstein para la gravedad, conocidas como las ecuaciones de campo de Einstein. Esta descripción es muy útil para entender el campo gravitatorio de objetos esféricos, como el Sol. También nos ayuda a comprender un tipo de agujero negro.

Matemáticamente, la métrica de Schwarzschild es solo una parte de una descripción más grande del espacio-tiempo con simetría esférica, llamada métrica de Kruskal-Schwarzschild. Sin embargo, esta solución más grande describe un espacio completamente vacío, por lo que no se usa para describir objetos físicos como estrellas o agujeros negros reales.

Historia de la Métrica de Schwarzschild

¿Quién descubrió la Métrica de Schwarzschild?

La solución de Schwarzschild lleva el nombre del físico alemán Karl Schwarzschild (1873-1916). Él encontró esta solución exacta en 1916, poco después de que Einstein publicara su teoría de la relatividad general. Fue la primera vez que se encontró una solución exacta a las ecuaciones de campo de Einstein, aparte de la solución simple del espacio vacío. Lamentablemente, Schwarzschild falleció poco después de publicar su trabajo, debido a una enfermedad que contrajo mientras servía en el ejército alemán durante la Primera Guerra Mundial.

Otro científico, Johannes Droste, llegó a la misma solución de forma independiente en 1916, usando un método más sencillo.

En los primeros años de la relatividad general, hubo mucha confusión sobre algunos puntos especiales (llamados singularidades) que aparecían en las soluciones de Schwarzschild. En su trabajo original, Schwarzschild colocó lo que hoy conocemos como el horizonte de sucesos en el centro de su sistema de coordenadas.

Entendiendo la Gravedad con la Métrica de Schwarzschild

¿Cómo describe la Métrica de Schwarzschild la gravedad?

El Sol y otras estrellas que giran lentamente tienen un campo gravitatorio que se puede describir bastante bien con la teoría de la gravedad de Isaac Newton. Según Newton, la fuerza de gravedad que siente un planeta a una distancia r del Sol es:

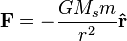
\mathbf{F} = -\frac{GM_sm}{r^2}\mathbf{\hat{r}}

Aquí, G es la constante de la gravedad, M es la masa del Sol y m es la masa del planeta.

Sin embargo, para algunos cálculos, la fórmula de Newton no es lo suficientemente precisa:

  • Por ejemplo, el planeta Mercurio tiene un movimiento especial en su órbita llamado avance del perihelio. Esto significa que el punto más cercano al Sol en cada órbita de Mercurio se mueve un poco con el tiempo. La teoría de Newton no podía explicar esto completamente.
  • Para estrellas muy densas, la forma del espacio alrededor de ellas se curva mucho, más de lo que predice Newton.

La Relatividad General de Einstein ofreció una nueva forma de entender la gravedad. Según Einstein, los planetas no son atraídos por una fuerza, sino que siguen los caminos más cortos (llamados geodésicas) en un espacio-tiempo que está curvado por la presencia de objetos masivos. Así, la gravedad se interpreta como un efecto de la curvatura del espacio-tiempo.

La métrica de Schwarzschild describe cómo se curva el espacio-tiempo alrededor de un objeto esférico. Esta descripción es mucho más precisa que la teoría de Newton y explica fenómenos que la teoría de Newton no podía (como el avance del perihelio).

¿Qué condiciones se necesitan para la Métrica de Schwarzschild?

Para encontrar esta solución, Schwarzschild partió de algunas condiciones matemáticas:

  1. Estática: El campo gravitatorio no cambia con el tiempo.
  2. Simetría esférica: El campo es igual en todas las direcciones alrededor del objeto, como una esfera perfecta.
  3. Espacio plano a grandes distancias: Muy lejos del objeto, el espacio-tiempo se comporta como si no hubiera gravedad, como el espacio-tiempo de Minkowski.

La Forma de la Métrica de Schwarzschild

En un sistema de coordenadas especial, la métrica de Schwarzschild se ve así:

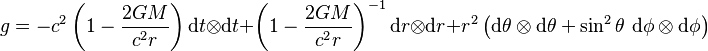
(1)g = -c^2 \left(1-\frac{2GM}{c^2 r} \right) \mathrm{d}t \otimes \mathrm{d}t + \left(1-\frac{2GM}{c^2 r}\right)^{-1}\mathrm{d}r\otimes \mathrm{d}r + r^2 \left(\mathrm{d}\theta\otimes \mathrm{d}\theta + \sin^2\theta\ \mathrm{d}\phi\otimes \mathrm{d}\phi \right)

Aquí, G es la constante de gravitación universal, M es la masa del objeto que crea la gravedad, y c es la velocidad de la luz. Esta fórmula describe cómo se mide la distancia y el tiempo en el espacio-tiempo curvado.

Existe otra forma de escribir esta métrica, llamada métrica de Kruskal, que permite describir más regiones del espacio-tiempo:

  • Región I: Es la región exterior, donde el campo gravitatorio se parece al de una estrella o planeta.
  • Región II: Es la región de un agujero negro.
  • Región III: Es la región de un agujero blanco, que es como un agujero negro al revés.
  • Región IV: Es otra región exterior, similar a la Región I, pero no conectada directamente.

Características del Espacio-Tiempo de Schwarzschild

¿Qué hay dentro del espacio-tiempo de Schwarzschild?

La métrica de Schwarzschild describe una región de espacio-tiempo que está completamente vacía fuera del objeto que crea la gravedad. Esto significa que no hay materia ni energía en esa región, solo la curvatura del espacio-tiempo causada por el objeto central.

¿Cómo se mueven los objetos en este espacio-tiempo?

Los objetos, como planetas o satélites, se mueven siguiendo caminos especiales llamados geodésicas. Estas geodésicas son las trayectorias más cortas en el espacio-tiempo curvado. Las ecuaciones que describen estas trayectorias son complejas, pero nos permiten predecir cómo se moverán los objetos bajo la influencia de la gravedad.

¿Qué simetrías tiene el espacio-tiempo de Schwarzschild?

La solución de Schwarzschild es simétrica en el tiempo (no cambia si el tiempo avanza o retrocede) y tiene simetría esférica (se ve igual desde cualquier dirección alrededor del centro).

Regiones del Espacio-Tiempo de Schwarzschild

Región I: Comparación con la teoría de Newton

La Región I de la solución de Schwarzschild describe el espacio-tiempo fuera de un objeto masivo. Las trayectorias de los planetas y satélites que predice son muy parecidas a las que predice la teoría de Newton a grandes distancias. Sin embargo, cerca del objeto, la métrica de Schwarzschild predice efectos nuevos y más precisos:

  • El avance del perihelio de planetas como Mercurio.
  • La curvatura o desviación de los rayos de luz al pasar cerca de objetos masivos.
  • El desplazamiento hacia el rojo de la luz debido a la gravedad.
  • El retraso de las ondas de radio o luz que atraviesan un campo gravitatorio.

La siguiente tabla muestra cómo se comparan las predicciones de la teoría de Newton y la solución de Schwarzschild para estos fenómenos:

Comparación de las predicciones de la teoría newtoniana y relativista de la gravitación
Teoría newtoniana Solución de Schwarzschild
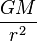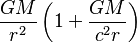Aceleración aparente respecto a un observador estático \frac{GM}{r^2} \, \frac{GM}{r^2}\left(1+\frac{GM}{c^2r}\right) \,
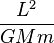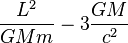Radio de una órbita circular \frac{L^2}{GMm} \, \frac{L^2}{GMm}-3\frac{GM}{c^2} \,
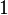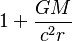Factor de desplazamiento al rojo gravitacional 1 \, 1 + \frac{GM}{c^2r} \,
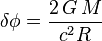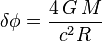Ángulo de deflexión de la luz \delta \phi = \frac{2 \, G \, M}{c^2R} \delta \phi = \frac{4 \, G \, M}{c^2R}
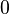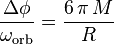Ritmo de precesión del perihelio 0 \, \frac{\Delta \phi}{\omega_{\rm orb}} = \frac{6 \, \pi \, M}{R}
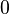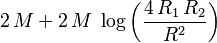Tiempo de retardo 0 \, 2 \, M + 2 \, M \; \log \left( \frac{4 \, R_1 \, R_2}{R^2} \right) \,

Donde L es el momento angular.

Región II: El Agujero Negro de Schwarzschild

Artículo principal: Agujero negro de Schwarzschild

Una de las cosas más fascinantes que predice la métrica de Schwarzschild es la existencia de agujeros negros. De hecho, las propiedades de esta solución fueron clave para desarrollar el concepto de agujero negro.

La solución de Schwarzschild muestra que si la masa de un objeto se concentra en un espacio muy pequeño, dentro de lo que se llama el radio de Schwarzschild, se forma una región del espacio-tiempo de la que nada puede escapar, ni siquiera la luz. Esta región es un agujero negro. Una vez que algo entra en un agujero negro, no puede salir.

Región III: El Agujero Blanco de Schwarzschild

Artículo principal: Agujero blanco

Esta región es como el opuesto de un agujero negro. En un agujero blanco, nada puede entrar, y todo lo que está dentro debe salir. Es una idea teórica, y no se cree que existan agujeros blancos en el universo real.

Región IV: Otra Región Exterior

Esta región es idéntica a la Región I, es decir, es una zona exterior al agujero negro donde el espacio es plano a grandes distancias. Sin embargo, no está conectada directamente con la Región I.

La solución completa de Schwarzschild a veces se visualiza como dos "universos paralelos" conectados por un "agujero de gusano" o "garganta" que se abre y se cierra. Sin embargo, la importancia física de las regiones III y IV es incierta, ya que los modelos de cómo se forman los agujeros negros (por ejemplo, por el colapso de una estrella) no suelen producir estas regiones.

Ver también

Véase también

Kids robot.svg En inglés: Schwarzschild metric Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Métrica_de_Schwarzschild&oldid=4942933»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Métrica de Schwarzschild para Niños. Enciclopedia Kiddle.