Clases de complejidad P y NP para niños
La relación entre las clases de complejidad NP y P es una pregunta muy importante en la teoría de la complejidad computacional. Fue planteada por primera vez por el científico Stephen Cook. En pocas palabras, la pregunta "¿Es P = NP?" significa: "Si podemos verificar rápidamente la solución de un problema, ¿podemos también encontrar esa solución rápidamente?". Aquí, "rápidamente" se refiere a un tiempo de cálculo que no crece demasiado a medida que el problema se hace más grande (conocido como "tiempo polinómico").
En la complejidad computacional, se estudian principalmente dos recursos:
- El tiempo: Se refiere a cuántos pasos necesita un algoritmo (una serie de instrucciones) para resolver un problema.
- El espacio: Se refiere a cuánta memoria usa el algoritmo para resolver el problema.
Los problemas se clasifican en grupos llamados clases de complejidad (como P y NP). Este artículo se centrará en las clases P y NP. Esta es considerada la pregunta más importante en este campo. El Clay Mathematics Institute ha ofrecido un premio de un millón de dólares estadounidenses a quien encuentre la primera respuesta correcta.
Contenido
¿Qué es el problema P vs NP?
Un ejemplo para entenderlo
Imagina el problema de la suma de subconjuntos. Te dan un grupo de números, por ejemplo, {−2, −3, 15, 14, 7, −10}. La pregunta es: ¿Existe algún subgrupo de estos números que sume 0?
- Encontrar la solución: Puede llevarte mucho tiempo probar todas las combinaciones posibles para encontrar un subgrupo que sume 0. Por ejemplo, {−2, −3, −10, 15} suma 0. Encontrar esto puede ser difícil si hay muchos números.
- Verificar la solución: Si alguien te dice: "Sí, el subgrupo {−2, −3, −10, 15} suma 0", es muy fácil y rápido comprobarlo. Solo tienes que sumar esos cuatro números.
La información que te permite verificar una respuesta (como el subgrupo {−2, −3, −10, 15}) se llama "certificado". Como puedes verificar la respuesta rápidamente (en tiempo polinómico) con un certificado, este problema se considera parte de la clase NP.
La pregunta P = NP busca saber si encontrar la solución es tan fácil como verificarla para problemas como el de la suma de subconjuntos. Si se demuestra que P no es igual a NP, significaría que algunos problemas NP son mucho más difíciles de resolver que de verificar.
Contexto del problema
La relación entre las clases P y NP se estudia en la teoría de la complejidad computacional. Esta parte de la teoría de la computación analiza los recursos (tiempo y memoria) que se necesitan para resolver un problema.
Para este análisis, se usa un modelo de computadora que funciona de forma "determinista" (siempre hace lo mismo con la misma información) y "secuencial" (hace una cosa después de otra). Este modelo representa bien cómo funcionan la mayoría de las computadoras.
Las clases de problemas P y NP
¿Qué es la clase P?
La clase P (de "Polinomial") incluye todos los problemas de decisión (aquellos que se responden con SÍ o NO) que una computadora normal puede resolver "rápidamente". "Rápidamente" significa en tiempo polinómico. Esto quiere decir que el tiempo que tarda en resolver el problema no crece de forma exagerada a medida que el tamaño del problema aumenta.
Intuitivamente, los problemas en P son los que consideramos "fáciles de resolver" o "manejables" en la práctica. Por ejemplo, encontrar el camino más corto entre dos puntos en un mapa o determinar si un ciclo pasa por cada línea de un dibujo una sola vez, son problemas en P.
¿Qué es la clase NP?
La clase NP (de "No determinista Polinomial") incluye problemas de decisión cuyas soluciones, si son correctas, pueden ser verificadas "rápidamente" (en tiempo polinómico). Esto significa que si alguien te da una posible solución, puedes comprobar si es correcta en poco tiempo.
Un ejemplo sencillo es el de la factorización de números. Si te preguntan si el número 323 es factorizable (si se puede dividir por otros números además de 1 y 323), puede que te lleve tiempo encontrar sus factores. Pero si alguien te dice "sí, porque 17 es un factor", puedes comprobarlo rápidamente dividiendo 323 entre 17. El número 17 es el "certificado" que te permite verificar la respuesta.
En una encuesta de 2002 a 100 investigadores, la mayoría (61) creía que P no es igual a NP. Solo 9 pensaban que sí lo era.
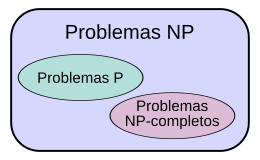
Problemas NP-Completos
Para entender mejor la pregunta P = NP, es muy útil el concepto de "completitud NP". Los problemas NP-completos son los problemas más "difíciles" dentro de la clase NP. Se cree que son los que tienen menos probabilidades de estar también en la clase P.
Si alguien encontrara una forma rápida de resolver un solo problema NP-completo, entonces automáticamente se podría resolver rápidamente cualquier otro problema en NP. Esto significaría que P = NP.
Un ejemplo famoso de problema NP-completo es el problema del viajante de comercio. Imagina a un vendedor que tiene que visitar varias ciudades y volver al punto de partida, pasando por cada ciudad una sola vez. El problema es encontrar la ruta más corta. Es fácil verificar si una ruta dada es válida y cuál es su longitud, pero encontrar la ruta más corta entre todas las posibles es increíblemente difícil si hay muchas ciudades.
El primer problema que se demostró ser NP-completo fue el problema de satisfacibilidad booleana (conocido como el teorema de Cook-Levin). Desde entonces, se ha demostrado que muchos otros problemas importantes son NP-completos, y hasta ahora, no se conoce ningún algoritmo rápido para resolverlos.
Soluciones propuestas
Muchos científicos han publicado trabajos intentando resolver el problema P vs NP. Es uno de los grandes desafíos de la informática.
Galería de imágenes
-
Diagrama de clases de complejidad para el caso en que P ≠ NP. La existencia de problemas fuera tanto de P como de NP-completos, fue determinada por Pichard T. Ledner.
Véase también
En inglés: P versus NP Facts for Kids
