Hexágono para niños
Datos para niños Hexágono |
||
|---|---|---|
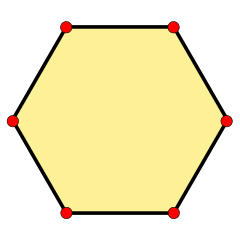 Un hexágono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 6 | |
| Vértices | 6 | |
| Grupo de simetría | 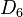 , orden 2x6 , orden 2x6 |
|
| Símbolo de Schläfli | {6}, t{3} (hexágono regular) | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Autodual | |
| Área |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{3\sqrt{3</td></tr><tr><td class="noprint" colspan="3" style="text-align:left;"></td></tr></table><!--IB_END--> [[Archivo:Regular polygon 6 annotated.svg|thumb|Un hexágono regular y sus ángulos principales]] [[Archivo:A 2-dimensional polytope.svg|thumb|Hexágono irregular]] En [[geometría]], un '''hexágono''' es una figura plana que tiene [[seis]] [[segmento|lados]] rectos y seis [[vértice (geometría)|puntos de esquina]] (vértices). Su nombre viene del [[griego antiguo|griego]] "hexágonon", que significa "seis ángulos". == Hexágono: Una Forma de Seis Lados == Un hexágono es un tipo de [[polígono]], que es una figura cerrada formada por líneas rectas. Los hexágonos pueden ser de muchas formas y tamaños, pero todos comparten la característica de tener seis lados y seis vértices. === Propiedades Básicas del Hexágono === Todos los hexágonos tienen algunas características en común: * Tienen 6 [[vértice (geometría)|vértices]] (puntos donde se unen dos lados). * Tienen 6 [[arista (geometría)|lados]] (las líneas rectas que forman la figura). * Tienen 9 [[Diagonal#Número de diagonales de un polígono|diagonales]]. Una diagonal es una línea que conecta dos vértices no consecutivos. * La suma de los [[ángulo interior#Suma de los ángulos interiores de un polígono|ángulos internos]] de cualquier hexágono siempre es 720 [[grado sexagesimal|grados]]. === El Hexágono Regular: Lados y Ángulos Iguales === [[Archivo:Sechseck-Zeichnung.svg|thumb|Medidas de un hexágono regular]] Un [[polígono regular|hexágono regular]] es un tipo especial de hexágono. Se caracteriza por tener: * Seis lados de la misma longitud. * Seis ángulos internos que miden exactamente lo mismo. Cada [[ángulo interno|ángulo interno]] de un hexágono regular mide 120 grados. Esto significa que si sumas todos sus ángulos internos (120° x 6), obtendrás 720 grados, como en cualquier hexágono. Los hexágonos regulares están muy relacionados con los [[triángulo equilátero|triángulos equiláteros]] (triángulos con los tres lados y ángulos iguales). Si unes el centro de un hexágono regular con cada uno de sus vértices, la figura se divide en seis triángulos equiláteros perfectos. Además, los hexágonos regulares son una de las pocas formas que pueden [[Teselado regular|cubrir completamente]] una superficie plana sin dejar huecos, al igual que los cuadrados y los triángulos equiláteros. Piensa en los panales de abejas, ¡son un ejemplo perfecto! ==== Cómo Calcular el Perímetro de un Hexágono Regular ==== El [[perímetro]] es la medida del contorno de una figura. Para un hexágono regular, como todos sus lados son iguales, calcular el perímetro es muy sencillo: * Multiplica la longitud de uno de sus lados por 6. * Fórmula: P = 6 × lado Por ejemplo, si un lado mide 5 cm, el perímetro será 6 × 5 = 30 cm. ==== Cómo Calcular el Área de un Hexágono Regular ==== El [[Área|área]] es la medida de la superficie que cubre una figura. Para un hexágono regular, puedes calcularla de varias maneras. Una forma es usar la longitud de su lado: * Fórmula: Área = <math>l^2 \frac{3\sqrt{3}}{2}
Esta fórmula se basa en que el hexágono regular se puede dividir en seis triángulos equiláteros. ContenidoCómo Dibujar un Hexágono Regular con Compás y ReglaPuedes dibujar un hexágono regular de forma precisa usando solo un regla y compás:
Simetría de los HexágonosUn hexágono regular es una figura muy simétrica. Esto significa que puedes doblarlo o girarlo de varias maneras y seguirá luciendo igual.
Existen diferentes tipos de hexágonos irregulares que tienen menos simetría que el regular, pero aún pueden tener algunas propiedades de simetría. Hexágonos en la Naturaleza y la TecnologíaLos hexágonos son formas muy comunes y eficientes, por eso los encontramos en muchos lugares, tanto en la naturaleza como en cosas hechas por el ser humano:
Véase también
|
|
















 En inglés:
En inglés: