Espacio topológico para niños

Un espacio topológico es una idea matemática que nos ayuda a entender cómo están "conectados" o "cerca" los puntos en un conjunto, sin necesidad de medir distancias. Imagina que tienes un grupo de puntos y quieres saber qué puntos están "alrededor" de otros o qué "regiones" forman. La topología nos da las reglas para definir esto.

La rama de las matemáticas que estudia los espacios topológicos se llama topología. Piensa en ella como el estudio de las formas y las conexiones que no cambian aunque estiremos o doblemos un objeto, siempre que no lo rompamos.

Espacio Topológico: ¿Qué es y para qué sirve?

Un espacio topológico es una forma de organizar un conjunto de elementos (llamados "puntos") para poder hablar de conceptos como la "cercanía", la "continuidad" (que algo no se rompa) o la "conexión" (que algo esté unido). A diferencia de los espacios métricos, que usan distancias para definir estas ideas, los espacios topológicos lo hacen de una manera más general, usando "conjuntos abiertos" o "vecindades".

Esto es útil en muchas áreas de las matemáticas y la ciencia. Por ejemplo, para entender cómo se comportan las funciones o las formas en diferentes situaciones.

Un poco de historia: ¿Quién lo inventó?

La idea de la topología empezó a tomar forma hace mucho tiempo. Alrededor de 1735, un matemático llamado Leonhard Euler descubrió una fórmula interesante para los poliedros (figuras con caras planas, como un cubo). Su fórmula Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V - E + F = 2 relaciona el número de vértices (esquinas), aristas (bordes) y caras. Esta fórmula fue un punto de partida para pensar en las propiedades de las formas que no cambian al deformarlas.

Más tarde, en el siglo XIX, matemáticos como Carl Friedrich Gauss, Bernhard Riemann, August Ferdinand Möbius y Camille Jordan empezaron a estudiar las superficies de una manera que se acercaba a la topología moderna. Querían saber cómo clasificar las superficies según sus propiedades de conexión, sin importar su tamaño o forma exacta.

El término "topología" fue introducido por Johann Benedict Listing en 1847. Sin embargo, fue Henri Poincaré quien, a finales del siglo XIX, sentó las bases de esta ciencia para espacios de cualquier dimensión.

Finalmente, la definición formal de los espacios topológicos, tal como los conocemos hoy, fue dada por Felix Hausdorff en 1914. Él fue quien popularizó la idea de "espacio métrico" y luego la generalizó a los espacios topológicos.

Entendiendo los Espacios Topológicos: Las Reglas del Juego

Un espacio topológico se forma con un conjunto de puntos y una colección especial de subconjuntos de que llamamos "topología" 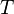. Esta colección 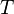debe seguir ciertas reglas.

Reglas con "Conjuntos Abiertos"

La forma más común de definir una topología es a través de los "conjuntos abiertos". Imagina que los conjuntos abiertos son como "regiones" o "vecindarios" dentro de tu conjunto . Para que una colección de subconjuntos sea una topología, debe cumplir estas tres reglas:

1. El conjunto vacío (un conjunto sin ningún punto) y el conjunto completo siempre deben ser conjuntos abiertos.
2. Si tienes varios conjuntos abiertos, no importa cuántos, la unión de todos ellos (es decir, juntarlos todos en uno solo) también debe ser un conjunto abierto.
3. Si tienes un número finito de conjuntos abiertos, la intersección de ellos (es decir, los puntos que están en todos ellos a la vez) también debe ser un conjunto abierto.

A los conjuntos que cumplen estas reglas se les llama "conjuntos abiertos" de ese espacio topológico. Los conjuntos que son el "complemento" de un conjunto abierto (todo lo que no está en el conjunto abierto) se llaman "conjuntos cerrados".

Reglas con "Vecindades"

Otra forma de entender un espacio topológico es a través de las "vecindades". Una vecindad de un punto es un conjunto que contiene a ese punto y algo de su "alrededor". Piensa en ello como un pequeño barrio alrededor de una casa. Las reglas para las vecindades son:

1. Cada punto debe estar dentro de todas sus propias vecindades.
2. Si un conjunto contiene una vecindad de un punto, entonces ese conjunto más grande también es una vecindad de ese punto.
3. La intersección (lo que tienen en común) de dos vecindades de un punto también es una vecindad de ese punto.
4. Dentro de cualquier vecindad de un punto, siempre puedes encontrar otra vecindad más pequeña de ese mismo punto, de tal manera que la vecindad grande sea también una vecindad para todos los puntos de la vecindad pequeña.

Si un conjunto es una vecindad para todos sus propios puntos, entonces ese conjunto es un "conjunto abierto".

Reglas con "Conjuntos Cerrados"

También podemos definir un espacio topológico usando los "conjuntos cerrados". Las reglas son muy parecidas a las de los conjuntos abiertos, pero al revés:

1. El conjunto vacío y el conjunto completo son conjuntos cerrados.
2. La intersección de cualquier cantidad de conjuntos cerrados (finitos o infinitos) también es un conjunto cerrado.
3. La unión de un número finito de conjuntos cerrados también es un conjunto cerrado.

Ejemplos Sencillos de Espacios Topológicos

Aquí tienes algunos ejemplos para entender mejor:

• Topología trivial o indiscreta: Es la más simple. Solo el conjunto vacío y el conjunto completo son considerados conjuntos abiertos.
• Topología discreta: Es la más "completa". Aquí, ¡cada subconjunto de es un conjunto abierto!
• Topología de los complementos finitos: En esta topología, los conjuntos abiertos son el conjunto vacío y todos los conjuntos cuyos "complementos" (lo que les falta para ser ) son finitos (tienen un número limitado de elementos).
• La recta real: Los números reales con la topología usual. Aquí, un conjunto es abierto si para cada punto dentro de él, puedes encontrar un pequeño intervalo abierto que contenga ese punto y que esté completamente dentro del conjunto.

¿Cómo se relaciona con la distancia?

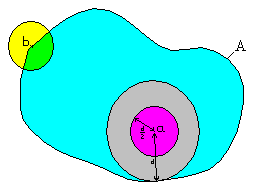
Muchos de los conceptos de la topología vienen de la idea de la distancia. Por ejemplo, en un espacio métrico (donde sí podemos medir distancias), podemos definir "bolas abiertas". Una bola abierta es el conjunto de todos los puntos que están a una distancia menor que un cierto radio de un punto central.

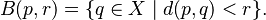
Estas bolas abiertas se usan para crear una topología. Sin embargo, no todas las topologías se pueden crear a partir de una distancia. Hay espacios topológicos donde no existe una forma de medir distancias de la manera usual. La topología es más general porque no necesita la idea de "distancia" para definir la "cercanía".

En esta imagen, el punto 'a' está en el interior del conjunto A, lo que significa que hay un espacio alrededor de 'a' que también está completamente dentro de A. El punto 'b' está en la frontera, porque cualquier "vecindad" alrededor de 'b' siempre toca tanto el conjunto A como lo que está fuera de A.

¿Qué propiedades tienen los Espacios Topológicos?

Los espacios topológicos pueden tener diferentes propiedades que los hacen únicos. Algunas de las más importantes son:

• Compacidad: Esta propiedad se relaciona con la idea de que un espacio no tiene "agujeros" o "bordes" infinitos, y se puede "cubrir" con un número finito de conjuntos abiertos.
• Conectividad: Un espacio es conexo si no se puede dividir en dos partes separadas. Piensa en una cuerda: es conexa. Si la cortas, ya no lo es.
• Axiomas de separación: Son reglas que nos dicen qué tan "separados" están los puntos o los conjuntos dentro de un espacio. Por ejemplo, si podemos encontrar vecindades que no se toquen para dos puntos diferentes.

Galería de imágenes

• 

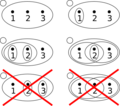
  Cuatro ejemplos de topologías y dos que no lo son, en el conjunto de tres puntos {1,2,3}.
  El ejemplo inferior izquierdo no es una topología porque la unión {2} y {3}, igual a {2,3}, no es parte de la colección.
  El ejemplo inferior derecho tampoco, porque la intersección de {1,2} y {2,3}, igual a {2}, no es parte de la colección.

Glosario y Más Información

• Glosario de topología
• Topología
• Conjunto abierto
• Conjunto cerrado
• Conjunto compacto
• Punto interior
• Punto frontera
• Punto exterior
• Punto aislado
• Punto de adherencia
• Punto de acumulación
• Interior (topología)
• Frontera (topología)
• Exterior (topología)
• Sucesión

Véase también

En inglés: Topological space Facts for Kids