Diámetro angular para niños
El diámetro angular es una forma de medir qué tan grande se ve un objeto desde donde lo estamos observando. Imagina que miras la Luna en el cielo: aunque es enorme, se ve pequeña porque está muy lejos. El diámetro angular nos dice el tamaño aparente de un objeto, como si lo midiéramos con un ángulo desde nuestros ojos.
Para medir el diámetro angular de objetos cercanos como el Sol, la Luna o los planetas, los científicos usan herramientas especiales. Para las estrellas más lejanas, usan técnicas más avanzadas. Si solo se mide la mitad de este ángulo (desde el centro del objeto hasta su borde), se le llama semidiámetro.
Contenido
¿Cómo se calcula el diámetro angular?
El tamaño aparente de un objeto depende de dos cosas: su tamaño real y qué tan lejos está de nosotros. Si un objeto es grande y está cerca, se verá muy grande. Si es pequeño y está lejos, se verá muy pequeño.
Los científicos usan fórmulas matemáticas para calcular el diámetro angular. Básicamente, si conoces el tamaño real de un objeto y la distancia a la que se encuentra, puedes saber qué tan grande se verá.
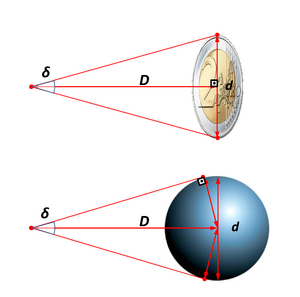
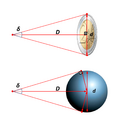
Por ejemplo, para un objeto con forma de disco, como una moneda, la fórmula considera su diámetro y la distancia a la que la miras. Para objetos con forma de esfera, como los planetas, la fórmula es un poco diferente porque sus bordes están un poco más cerca de ti que su centro. Sin embargo, para objetos muy lejanos, como las estrellas, la diferencia entre estas fórmulas es mínima.
¿Cómo estimar el diámetro angular con tu mano?
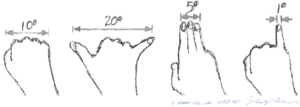
Puedes hacer una estimación rápida de algunos diámetros angulares usando tu mano con el brazo completamente estirado. Mira la imagen para ver cómo:
- Un puño cerrado puede cubrir unos 10 grados.
- Tu mano abierta, con los dedos estirados, puede cubrir unos 20 grados.
- Tres dedos juntos (índice, corazón y anular) pueden cubrir unos 5 grados.
- Tu dedo meñique puede cubrir aproximadamente 1 grado.
Esta es una forma divertida y sencilla de tener una idea de los tamaños aparentes en el cielo.
El diámetro angular en la astronomía
En la astronomía, el diámetro angular es muy importante. Nos ayuda a entender cómo se ven los objetos celestes desde la Tierra. Como estos ángulos suelen ser muy pequeños, los astrónomos usan unidades especiales:
- Un grado (°) se divide en 60 minutos de arco (′).
- Cada minuto de arco se divide en 60 segundos de arco (″).
Así, un segundo de arco es una medida muy, muy pequeña, ¡como dividir un grado en 3600 partes!
Por ejemplo:
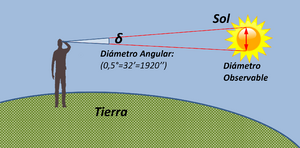
- El Sol y la Luna se ven casi del mismo tamaño en el cielo desde la Tierra. Ambos tienen un diámetro angular de aproximadamente medio grado, o unos 30 minutos de arco. Por eso, durante un eclipse solar total, la Luna puede cubrir completamente al Sol.
- El diámetro angular del Sol, visto desde la Tierra, es de unos 32 minutos de arco.
- El diámetro angular de Sirio, una estrella muy brillante, es mucho más pequeño que el del Sol, aunque Sirio es más grande que nuestro Sol. Esto se debe a que Sirio está muchísimo más lejos.
Tamaños angulares de objetos celestes
Esta tabla muestra qué tan grandes se ven algunos cuerpos celestes desde la Tierra:
| Cuerpo celeste | Diámetro angular o tamaño | Tamaño relativo (mínimo y máximo) |
|---|---|---|
| Sol | 31′31″-32′33″ | 30-31 veces el máximo valor para Venus (barra naranja debajo) / 1891-1953″ |
| Luna | 29′20″-34′6″ | 28-32,5 veces el máximo valor para Venus (barra naranja debajo) / 1760-2046″ |
| Nebulosa de la Hélice | 16′-28′ | 15,2-26,6 veces el máximo valor para Venus (barra naranja debajo) / 960-1680″ |
| Espiral en la Nebulosa del Águila | 4′40″ | 4,44 veces el máximo valor para Venus (barra naranja debajo) / 280″ |
| Venus | 9,67″-63,00″ |
|
| Júpiter | 29,80″-49,06″ |
|
| Saturno | 14,50″-19,92″ |
|
| Marte | 3,50″-25,08″ |
|
| Mercurio | 4,54″-13,02″ |
|
| Urano | 3,31″-4,04″ |
|
| Neptuno | 2,17″-2,36″ |
|
| Ceres | 0,33″-0,84″ |
|
| Asteroide Vesta | 0,20″-0,64″ |
|
| Plutón | 0,063″-0,115″ |
|
| R Doradus | 0,052″-0,062″ |
|
| Betelgeuse | 0,049″-0,060″ |
|
| Eris | 0,034″-0,089″ |
|
| Alfard | 0,00909″ |
|
| Alfa Centauri A | 0,007″ |
|
| Canopus | 0,006″ |
|
| Sirio | 0,005936″ |
|
| Altair | 0,003″ |
|
| Deneb | 0,002″ |
|
| Próxima Centauri | 0,001″ |
|
| Alnitak | 0,0005″ | |
| Una estrella como Alnitak está a una distancia tal que el telescopio espacial Hubble se encuentra en el límite de poder observar su diámetro angular. | 6×10-10″ |
- Aunque Plutón es más grande que Ceres en tamaño real, desde la Tierra, Ceres se ve más grande. Esto es porque Ceres está mucho más cerca de nosotros.
- Las tres estrellas del cinturón de Orión cubren un ángulo de unos 4.5 grados en el cielo.
¿Cómo se usa el diámetro angular para medir distancias?
A veces, los astrónomos no pueden medir directamente la distancia a un objeto muy lejano. Pero si saben el tamaño real de ese objeto (porque es similar a otros objetos que sí conocen) y pueden medir su diámetro angular, ¡pueden calcular qué tan lejos está!
La fórmula se invierte para encontrar la distancia: si conoces el tamaño real del objeto y su diámetro angular, puedes saber la distancia a la que se encuentra de la Tierra.
Objetos que no son circulares
No todos los objetos en el espacio son perfectamente circulares. Muchas galaxias y nebulosas tienen formas irregulares. En estos casos, los astrónomos dan dos medidas de diámetro angular: una para su parte más larga y otra para su parte más corta. Por ejemplo, la Pequeña Nube de Magallanes se ve como un óvalo en el cielo.
Ejemplos de diámetro angular
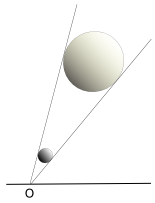
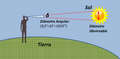
Como se ve en la imagen, dos objetos de tamaños muy diferentes pueden parecer del mismo tamaño si uno es mucho más grande pero está más lejos.
Imagina una moneda de 2 euros para entender mejor el diámetro angular:
- Si la pones a 1.5 metros de distancia, su diámetro angular es de 1 grado.
- Si la pones a casi 90 metros, su diámetro angular es de 1 minuto de arco.
- Si la pones a poco más de 5 kilómetros, su diámetro angular es de 1 segundo de arco.
Esto te ayuda a entender lo pequeños que son los segundos de arco y por qué son útiles para medir objetos muy lejanos en el espacio.
Galería de imágenes
-
Cálculo del diámetro angular en un disco y en una esfera
-
Ángulos aproximados de 10°, 20°, 5° y 1° en la mano respecto al brazo extendido
-
Diámetro angular: ángulo subtendido por el Sol desde la Tierra
-
Carta de comparación del diámetro angular del Sol, la Luna y los planetas.
-
Figura 1. El diámetro angular nos da una medida aparente de la dimensión de los cuerpos celestes.
Véase también
En inglés: Angular diameter Facts for Kids
- Separación angular
- Ángulo sólido
- Resolución óptica
- Agudeza visual
