Ecuaciones de Lotka-Volterra para niños
Las ecuaciones de Lotka-Volterra, también conocidas como ecuaciones depredador-presa, son un conjunto de fórmulas matemáticas que nos ayudan a entender cómo cambian las poblaciones de dos especies que interactúan entre sí: una que es la presa (el animal que es comido) y otra que es el depredador (el animal que come a la presa).
Estas ecuaciones fueron propuestas de forma independiente por dos científicos: Alfred J. Lotka en 1925 y Vito Volterra en 1926. Nos muestran cómo el número de individuos de cada especie sube y baja con el tiempo, creando ciclos.
Las ecuaciones se ven así:
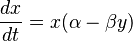
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{dy}{dt} = - y(\gamma - \delta x)
Donde:
- y es el número de depredadores (por ejemplo, lobos).
- x es el número de presas (por ejemplo, conejos).
- dx/dt y dy/dt nos dicen cómo cambian las poblaciones de presas y depredadores con el tiempo.
- t representa el tiempo.
- α, β, γ y δ son números (parámetros) que representan cómo interactúan las dos especies, como la tasa de nacimiento de las presas o la eficiencia de los depredadores para cazar.
Contenido
¿Quién las descubrió y por qué?
El modelo de Lotka-Volterra fue pensado por primera vez por Alfred J. Lotka en 1910, cuando estudiaba reacciones químicas. Luego, en 1920, Lotka aplicó estas ideas a sistemas biológicos, usando como ejemplo una planta y un animal que la come. En 1925, publicó estas ecuaciones para analizar cómo interactúan los depredadores y sus presas en un libro sobre matemáticas aplicadas a la biología.
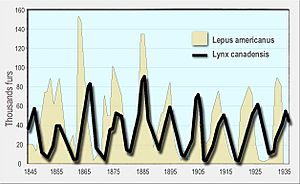
El mismo conjunto de ecuaciones fue publicado en 1926 por Vito Volterra, un matemático y físico que se interesó por la biología. La investigación de Volterra surgió de sus conversaciones con el biólogo marino Umberto D'Ancona. D'Ancona había notado algo curioso: durante la Primera Guerra Mundial (1914-1918), cuando se pescaba menos en el mar Adriático, el porcentaje de peces depredadores capturados ¡había aumentado! Esto le parecía extraño. Volterra desarrolló su modelo para explicar esta observación de D'Ancona.
Un ejemplo sencillo: Babuinos y Guepardos
Imaginemos que tenemos dos especies: babuinos (la presa) y guepardos (el depredador). Si al principio hay 10 babuinos y 10 guepardos, podemos usar las ecuaciones para ver cómo cambian sus poblaciones. Por ejemplo, si los babuinos se reproducen rápido y los guepardos cazan bien, veremos cómo sus números suben y bajan en un ciclo.
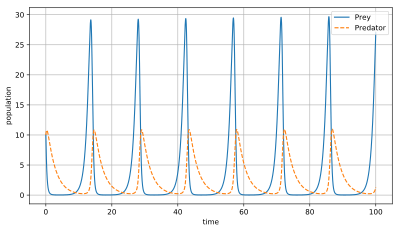
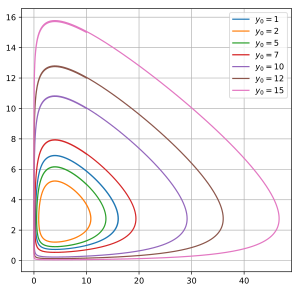
También podemos ver estas relaciones en un gráfico especial llamado "espacio de fase". En este gráfico, un eje muestra el número de presas y el otro el número de depredadores. Las líneas en el gráfico muestran cómo las poblaciones se mueven en un ciclo cerrado, sin necesidad de ver el tiempo directamente.
¿Cómo cambian las poblaciones con el tiempo?
En este modelo, los depredadores tienen muchos alimentos cuando hay muchas presas. Pero si los depredadores se multiplican demasiado, pueden comer tantas presas que su alimento empieza a escasear, y entonces la población de depredadores disminuye. Cuando hay pocos depredadores, la población de presas puede volver a crecer. Así, estas poblaciones siguen un ciclo de crecimiento y disminución.
Puntos de equilibrio: ¿Cuándo no cambian las poblaciones?
El equilibrio en este modelo ocurre cuando el número de presas y depredadores no cambia. Esto sucede cuando las ecuaciones dan como resultado cero, es decir, cuando las poblaciones se mantienen estables.
Hay dos situaciones de equilibrio:
- La primera es cuando ambas especies desaparecen (0 presas y 0 depredadores). Si no hay animales, no hay cambios.
- La segunda es un punto donde ambas poblaciones se mantienen en un número constante, sin desaparecer. Este punto depende de los valores de los parámetros (α, β, γ, δ) que representan cómo interactúan.
¿Qué pasa si una especie desaparece?
El modelo nos dice que es muy difícil que ambas especies desaparezcan por completo. Si solo una especie desaparece, por ejemplo, si los depredadores se extinguen, la población de presas crecería sin límites en este modelo simple. Pero si las presas desaparecen, los depredadores morirían de hambre. Sin embargo, si las poblaciones se acercan mucho a cero, el modelo sugiere que aún podrían recuperarse.
¿Por qué las poblaciones suben y bajan en ciclos?
Alrededor del punto de equilibrio donde ambas especies existen, las poblaciones de depredadores y presas no se quedan quietas. En cambio, sus números suben y bajan en ciclos, como una onda. Esto significa que las soluciones de las ecuaciones son periódicas, es decir, se repiten una y otra vez. Las poblaciones oscilan alrededor del punto de equilibrio, sin detenerse.
Explicación de las ecuaciones
Las ecuaciones de Lotka-Volterra nos ayudan a entender cómo la cantidad de presas y depredadores cambia en un ecosistema.
La población de la presa
La primera ecuación es para la presa:
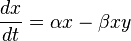
Esta ecuación asume que las presas tienen comida ilimitada y se reproducen muy rápido (crecimiento exponencial), a menos que haya depredadores. El término αx representa este crecimiento rápido. El término βxy representa cuántas presas son cazadas por los depredadores. Si no hay presas (x=0) o no hay depredadores (y=0), no hay interacción.
En resumen, el cambio en el número de presas es igual a su propio crecimiento menos las que son cazadas por los depredadores.
La población del depredador
La segunda ecuación es para el depredador:
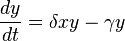
En esta ecuación, δxy representa cómo crece la población de depredadores, ya que su crecimiento depende de cuántas presas cazan. El término γy representa la muerte natural de los depredadores. Cuantos más depredadores hay, más presas necesitan para sobrevivir y mantener su población.
En resumen, el cambio en el número de depredadores es igual a su crecimiento por la caza de presas menos las muertes naturales.
Véase también
 En inglés: Lotka–Volterra equations Facts for Kids
En inglés: Lotka–Volterra equations Facts for Kids