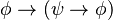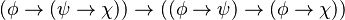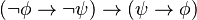Axioma para niños
Un axioma es una idea o afirmación tan fundamental y clara que se acepta como verdadera sin necesidad de ser demostrada. Piensa en ellos como los cimientos de un edificio: son la base sólida sobre la que se construye todo lo demás en campos como las matemáticas o la lógica.
En las matemáticas y otras ciencias, un axioma es uno de esos principios básicos e imposibles de demostrar, a partir de los cuales se desarrolla toda una teoría usando el razonamiento lógico.
En la investigación, un axioma es una afirmación que se toma como punto de partida dentro de un conjunto de ideas, y sobre la cual se apoyan otros razonamientos y conclusiones.
Contenido
Qué es un Axioma: La Base del Conocimiento
Originalmente, los matemáticos griegos antiguos consideraban un axioma como una afirmación "evidente" que se aceptaba sin pruebas. Hoy en día, en un sistema de pensamiento lógico, un axioma es una afirmación que no se deduce de otras, sino que es una regla general del pensamiento. En lógica y matemáticas, un axioma es simplemente una idea que se asume como verdadera, sin importar si es obvia o no, y se usa para demostrar otras afirmaciones.
Actualmente, se investiga qué consecuencias lógicas tienen diferentes conjuntos de axiomas. A veces, se puede elegir un axioma o su opuesto, y ninguna de las dos opciones parece más "evidente". Así, mientras que antes los axiomas se elegían por ser "afirmaciones obvias" para deducir el resto de las ideas, en la teoría de modelos moderna, un axioma es solo una suposición. Su verdad o falsedad no depende de si nos parece intuitivo o autoevidente.
En lógica, un postulado es una afirmación que no tiene por qué ser evidente. Es una frase bien construida de un lenguaje formal que se usa en un razonamiento para llegar a una conclusión. Los axiomas no lógicos también pueden llamarse "postulados" o "suposiciones". Un axioma no lógico es una expresión lógica formal que se usa para construir una teoría matemática, y puede o no ser obvia por sí misma. Un ejemplo es el postulado paralelo en la geometría euclidiana.
Axiomatizar un sistema de conocimiento significa mostrar que sus afirmaciones pueden obtenerse de un pequeño grupo de ideas bien entendidas (los axiomas). Generalmente, hay muchas formas de organizar un área matemática con axiomas. Cualquier axioma es una afirmación que sirve como punto de partida para deducir otras afirmaciones de forma lógica. Si un axioma es "verdadero" y qué significa eso, es un tema de debate en la filosofía de las matemáticas.
Origen e Historia de los Axiomas
La palabra axioma viene del griego antiguo ἀξίωμα, que significa "lo que parece justo" o "lo que se considera evidente". Procede del verbo griego ἀξιόειν (axioein), que significa "valorar", y a su vez de ἄξιος (axios): "valioso" o "digno". Para los filósofos griegos antiguos, un axioma era algo que parecía verdadero sin necesidad de prueba.
La palabra postulado significa "exigir". Por ejemplo, Euclides "exige" que estemos de acuerdo en que algunas cosas se pueden hacer, como unir dos puntos con una línea recta. Los antiguos geómetras distinguían entre axiomas y postulados. Proclus, al comentar los libros de Euclides, menciona que Gemino pensaba que el cuarto postulado de Euclides debería ser un axioma, porque no afirma la posibilidad de una construcción, sino una propiedad esencial.
El Legado de los Griegos Antiguos
Uno de los grandes logros de los matemáticos griegos fue organizar las afirmaciones y teoremas matemáticos de forma lógica y coherente. Lo hicieron a partir de un pequeño número de postulados o axiomas muy sencillos. Estos son los conocidos axiomas de la geometría o las reglas de la aritmética. Los objetos matemáticos se crearon como ideas abstractas o idealizaciones de la realidad física. Los axiomas, ya sea que se acepten como "evidentes" o simplemente como muy probables, se aceptan sin demostración. Sobre ellos se ha construido la estructura de las matemáticas.
El método lógico-deductivo, donde las conclusiones se obtienen de ideas iniciales mediante argumentos sólidos, fue desarrollado por los griegos antiguos. Este método es el principio básico de las matemáticas modernas. Sin suposiciones iniciales, no se puede deducir nada. Por lo tanto, los axiomas y postulados son las suposiciones básicas de cualquier conocimiento deductivo. Se aceptan sin demostración. Todas las demás afirmaciones, como los teoremas en matemáticas, deben demostrarse con la ayuda de estas suposiciones básicas.
Sin embargo, la forma de entender el conocimiento matemático ha cambiado desde la antigüedad. Por eso, los términos axioma y postulado tienen un significado ligeramente diferente para los matemáticos de hoy que para Aristóteles y Euclides.
Los antiguos griegos veían la geometría como una ciencia y consideraban los teoremas geométricos como hechos científicos. Usaron el método lógico-deductivo para evitar errores y organizar el conocimiento. La obra Segundos analíticos de Aristóteles explica muy bien este punto de vista clásico.
Un "axioma", en la terminología clásica, era una suposición evidente común a muchas ramas de la ciencia. Un buen ejemplo sería la afirmación: Cuando se quita una cantidad igual de cosas iguales, lo que queda es una cantidad igual.
Además de los axiomas, en la base de las ciencias había otras suposiciones que se aceptaban sin pruebas. Estas se llamaban postulados. Mientras que los axiomas eran comunes a muchas ciencias, los postulados de cada ciencia eran diferentes. Su validez debía confirmarse con la experiencia del mundo real. Aristóteles decía que el contenido de una ciencia no se puede enseñar bien si el estudiante duda de la verdad de los postulados.
El enfoque clásico se ve claramente en los Elementos de Euclides, donde hay una lista de postulados (hechos geométricos de sentido común basados en nuestra experiencia), seguida de una lista de "nociones comunes" (afirmaciones muy básicas y evidentes).
Postulados de Euclides
- Es posible dibujar una línea recta desde cualquier punto a cualquier otro punto.
- Es posible extender un segmento de recta continuamente en ambas direcciones.
- Es posible dibujar una circunferencia con cualquier centro y cualquier radio.
- Todos los ángulos rectos son iguales entre sí.
- (Postulado de las paralelas) Si una línea corta a otras dos líneas y hace que los ángulos interiores de un mismo lado sumen menos de dos ángulos rectos, entonces esas dos líneas, si se extienden indefinidamente, se cruzarán en ese lado donde los ángulos son menores que dos ángulos rectos.
Nociones Comunes de Euclides
- Las cosas que son iguales a la misma cosa, también son iguales entre sí.
- Si se suman cantidades iguales a cantidades iguales, los resultados son iguales.
- Si se restan cantidades iguales de cantidades iguales, los resultados son iguales.
- Las cosas que coinciden son iguales entre sí.
- El todo es mayor que la parte.
Axiomas en Lógica
En lógica, un axioma es una afirmación que se considera verdadera por sí misma. A partir de ella, se deducen otras afirmaciones usando el método deductivo, lo que lleva a conclusiones que son coherentes con el axioma. A partir de los axiomas y de las reglas de inferencia, se deben deducir todas las demás afirmaciones de una teoría.
Axioma Lógico
Los axiomas lógicos son ciertas fórmulas en un lenguaje formal que son siempre válidas. Esto significa que son verdaderas en cualquier situación posible. Generalmente, se elige un conjunto mínimo de afirmaciones que son siempre verdaderas (llamadas tautologías) y que son suficientes para probar una teoría.
Ejemplo de Axiomas Lógicos
En el cálculo proposicional, es común usar como axiomas lógicos todas las fórmulas siguientes:
Donde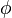 
, 
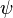, y 
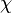pueden ser cualquier fórmula en el lenguaje.
Cada uno de estos es un esquema de axiomas, una regla para crear un número infinito de axiomas. Por ejemplo, si p, q y r son variables, entonces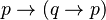 
es un axioma. Se puede demostrar que con estos tres esquemas de axiomas y la regla de inferencia modus ponens, todas las tautologías del cálculo proposicional se pueden probar.
Axiomas en Matemáticas
En matemáticas, para que una afirmación sea considerada válida, debe estar incluida en un grupo de afirmaciones iniciales (los axiomas) o debe poder demostrarse a partir de ellos. Los axiomas son, por lo tanto, los pilares fundamentales de cada rama de las matemáticas. A partir de ellos, y mediante demostraciones, se comprueba la verdad de cualquier afirmación.
Los axiomas son afirmaciones que se aceptan como verdaderas y cuya verdad no puede demostrarse a partir de otros axiomas. Un axioma no se define por ser obvio o intuitivo; el axioma de elección es un ejemplo de un axioma que no es trivial.
El otro tipo de afirmaciones son los teoremas. Estas afirmaciones deben demostrarse usando los axiomas u otros teoremas ya probados. Una consecuencia directa de un teorema se llama corolario.
Muchas partes de las matemáticas están organizadas con axiomas. Esto significa que hay un conjunto de axiomas de los cuales se pueden deducir todas las verdades de esa parte de las matemáticas. Por ejemplo, de los axiomas de Peano se pueden deducir todas las verdades de la aritmética.
El formalismo que surgió a principios del siglo XX llevó al programa de Hilbert. Este programa buscaba organizar diferentes ramas de las matemáticas usando un conjunto de axiomas claros, generalmente escritos en lenguajes formales de primer orden. Esto significaba que, junto con los axiomas lógicos normales, se introducían símbolos especiales y ciertos axiomas matemáticos que usaban esos símbolos para definir su comportamiento. Cada teoría matemática necesita un conjunto diferente de símbolos especiales. Por ejemplo, la aritmética de primer orden necesita la función "siguiente" y una constante para el primer número natural.
El programa de Hilbert hizo pensar que las matemáticas podrían ser un sistema donde la propia consistencia de los axiomas elegidos fuera fácil de verificar. Sin embargo, los teoremas de incompletitud de Gödel y otros resultados mostraron que el programa de Hilbert no era viable para los fines que se propuso.
Limitaciones de los Sistemas Axiomáticos
A mediados del siglo XX, Kurt Gödel demostró sus famosos teoremas de incompletitud. Estos teoremas mostraron que, incluso si un sistema de axiomas recursivos estaba bien definido y era consistente, los sistemas axiomáticos con esos axiomas tienen limitaciones importantes. Es importante que el conjunto de axiomas sea recursivamente enumerable, lo que significa que se puede verificar si una afirmación es un axioma.
Con esa condición, Gödel demostró que si una teoría tiene un modelo de cierta complejidad, siempre hay una afirmación P que es verdadera pero no se puede demostrar dentro de ese sistema. Gödel probó que en cualquier sistema formal que incluya aritmética, se puede crear una proposición P que diga: "este enunciado no se puede demostrar".
Véase también
En inglés: Axiom Facts for Kids
- Sistema axiomático
- Axiomas de Zermelo-Fraenkel
- Postulado
- Principio
- Dogma
- Sistema formal
- Regla de inferencia
- Conjetura
- Teorema
- Axiomas de Peano
- Teoremas de incompletitud de Gödel
- Axiomas de Hilbert
