Recta para niños
En geometría, una recta es una línea que se extiende sin fin en una sola dirección. Imagina una cuerda muy, muy larga y perfectamente estirada que nunca termina. Una recta tiene solo una dimensión (largo) y está formada por un número infinito de puntos muy juntos.
La recta es uno de los conceptos más importantes en geometría, junto con el punto y el plano. Son ideas tan básicas que se usan para definir otras cosas. Las rectas suelen nombrarse con una letra minúscula.
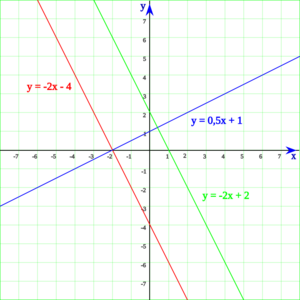
En geometría analítica, que usa números para describir formas, las rectas en un plano se pueden representar con una ecuación sencilla: y = m x + b. Aquí, x e y son las coordenadas de los puntos en un plano cartesiano. La letra m se llama "pendiente" y nos dice qué tan inclinada está la recta. La letra b es el "término independiente" y nos dice dónde la recta cruza el eje vertical (el eje y).
Contenido
¿Qué es una Recta? Definiciones Clave
Euclides, un famoso matemático de la antigüedad, escribió un libro llamado Los Elementos donde definió la línea y la recta:
- Una línea es algo que tiene longitud pero no anchura.
- Los extremos de una línea son puntos.
- Una línea recta es aquella que se extiende de manera uniforme entre los puntos que la forman.
Características Principales de una Recta
Las rectas tienen propiedades muy interesantes:
- Una recta se extiende sin fin en ambas direcciones.
- En la geometría que estudiamos normalmente (geometría euclidiana), la distancia más corta entre dos puntos siempre es una línea recta.
- Una recta también puede verse como el conjunto de puntos donde se encuentran dos planos.
¿Qué es una Semirrecta?
Una semirrecta es una parte de una recta. Imagina que cortas una recta en un punto. Cada una de las dos partes que quedan es una semirrecta. Tiene un punto de inicio, llamado origen, y se extiende indefinidamente en una sola dirección.
Semirrecta Opuesta: Un Par Especial
La semirrecta opuesta es la otra parte de la recta que se forma cuando la cortas.
- Cada semirrecta tiene solo una semirrecta opuesta.
- Una semirrecta y su semirrecta opuesta siempre comparten el mismo punto de origen.
Ecuación de la Recta en el Plano Cartesiano
En un plano cartesiano, podemos describir una recta usando ecuaciones. Esto nos permite saber dónde está cada punto de la recta.
Entendiendo la Pendiente y la Ordenada al Origen
La forma más común de escribir la ecuación de una recta es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = m x + b
- m es la pendiente: Nos dice qué tan inclinada está la recta. Si la pendiente es positiva, la recta sube de izquierda a derecha. Si es negativa, baja. Si es cero, es horizontal.
- b es la ordenada al origen: Es el punto donde la recta cruza el eje vertical (el eje y).
Ejemplo Práctico
Imagina que tienes una recta que pasa por el punto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A=(-5,3) y tiene una pendiente de 
. Podemos usar la fórmula 
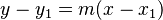para encontrar su ecuación. Sustituyendo los valores: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y - 3 = 6 (x - (-5)) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y - 3 = 6 (x + 5) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y - 3 = 6x + 30 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 6x + 30 + 3 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 6x + 33 Esta es la ecuación de la recta. Si pones un valor de x, obtendrás el valor de y que le corresponde en esa recta.
Otras Formas de la Ecuación de la Recta
Existen otras maneras de escribir la ecuación de una recta, dependiendo de la información que tengamos:
- Forma Simplificada (Pendiente-Ordenada al Origen): Si conoces la pendiente (m) y el punto donde la recta corta el eje y (0, b), la ecuación es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = m x + b .
- Forma Segmentaria (Ecuación Simétrica): Si sabes dónde la recta corta el eje x (en a) y el eje y (en b), la ecuación es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x}{a} + \frac{y}{b} = 1 .
- Ecuación General: Una forma más general de escribir la ecuación de una recta es
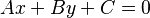. Aquí, A, B y C son números.
Rectas Notables y sus Relaciones
Algunas rectas tienen características especiales:
- Recta Vertical: Su ecuación es
, donde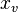 
es un número constante. Por ejemplo, 
es una línea vertical que pasa por el 3 en el eje x. - Recta Horizontal: Su ecuación es
, donde Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_h es un número constante. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 5 es una línea horizontal que pasa por el 5 en el eje y. - Recta que Pasa por el Origen: Si una recta pasa por el punto (0,0), su ecuación es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = m x (la b es cero).
Relaciones entre Dos Rectas
Cuando tenemos dos rectas, pueden estar relacionadas de varias maneras:
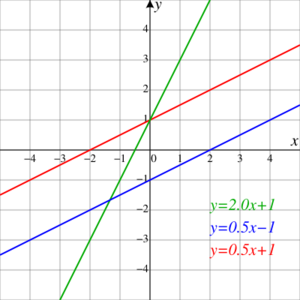
- Rectas Paralelas: Son rectas que nunca se cruzan, siempre mantienen la misma distancia entre sí. Esto ocurre si tienen la misma pendiente (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): m_1 = m_2 ).
- Rectas Perpendiculares: Son rectas que se cruzan formando un ángulo de 90 grados (un ángulo recto). Esto sucede si la pendiente de una es el inverso negativo de la otra (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): m_1 = -1/ m_2 ).
- Rectas Secantes: Son rectas que se cruzan en un solo punto.
- Rectas Tangentes: Son rectas que tocan una curva en un solo punto, sin "atravesarla".
Rectas en el Espacio (3D)
Las rectas no solo existen en un plano (2D), también pueden existir en el espacio (3D).
- Una recta en el espacio puede describirse como la intersección de dos planos. Imagina dos paredes que se unen en una esquina; la línea donde se encuentran es una recta en 3D.
- También se puede definir una recta en el espacio con un punto por el que pasa y un "vector director" que indica su dirección.
Posiciones de Rectas en el Espacio
En 3D, las rectas pueden:
- Ser paralelas: Nunca se tocan y van en la misma dirección.
- Ser coincidentes: Son la misma recta.
- Intersecarse: Se cruzan en un solo punto.
- Cruzarse: No son paralelas y tampoco se tocan. Imagina dos aviones volando en diferentes alturas y direcciones; sus trayectorias se cruzan pero no chocan.
Véase también
En inglés: Line Facts for Kids
