Álgebra homológica para niños
El álgebra homológica es una rama de las matemáticas que usa herramientas del álgebra para estudiar la homología. La homología es una forma de entender las "formas" o "agujeros" en objetos matemáticos, como si fueran figuras geométricas.
Esta área de las matemáticas es relativamente nueva. Sus inicios se encuentran en investigaciones de finales del siglo XIX sobre la topología combinatoria (que es como una versión anterior de la topología algebraica) y el álgebra abstracta (especialmente la teoría de módulos). Matemáticos importantes como Henri Poincaré y David Hilbert fueron pioneros en estas ideas.
Se considera que el álgebra homológica moderna comenzó con la publicación del libro Homological Algebra de Henri Cartan y Samuel Eilenberg en 1956. Más tarde, Alexander Grothendieck hizo contribuciones importantes, extendiendo estas ideas a las categorías abelianas. Por eso, el desarrollo del álgebra homológica está muy relacionado con la aparición de la teoría de categorías, que es una forma de organizar y relacionar diferentes estructuras matemáticas.
Contenido
Cadenas complejas y homología
La idea principal en el álgebra homológica es la de una cadena compleja. Imagina una secuencia de grupos abelianos (conjuntos de números que se pueden sumar) conectados por "mapas" (reglas que transforman elementos de un grupo en otro).
Una cadena compleja se ve así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): C_\bullet: \cdots \longrightarrow C_{n+1} \stackrel{d_{n+1}}{\longrightarrow} C_n \stackrel{d_n}{\longrightarrow} C_{n-1} \stackrel{d_{n-1}}{\longrightarrow} \cdots
Aquí, los C son los grupos y los d son los mapas. La característica especial es que si aplicas dos mapas seguidos, el resultado siempre es cero: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d_n \circ d_{n+1}=0.
Los elementos de Cn se llaman n-cadenas, y los mapas dn se llaman mapas de límites o diferenciales.
Dentro de cada grupo Cn, podemos identificar dos tipos de elementos:
- Los ciclos (Zn): Son los elementos que, al aplicar el mapa dn, se convierten en cero.
- Los límites (Bn): Son los elementos que son el resultado de aplicar el mapa dn+1.
Debido a la propiedad Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d_n \circ d_{n+1}=0 , todos los límites son también ciclos. Esto significa que los límites están "dentro" de los ciclos: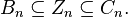 
Los grupos de homología Hn(C) se forman tomando los ciclos y "eliminando" los límites. Es como decir: "De todos los ciclos, ¿cuáles son realmente 'agujeros' y no solo bordes de algo más grande?". Se calculan como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): H_n(C) = Z_n/B_n
Si todos los grupos de homología de una cadena compleja son cero, se dice que es acíclica o una sucesión exacta.
Las cadenas complejas aparecen en muchas áreas de las matemáticas. Por ejemplo:
- Si tienes una forma geométrica X, puedes construir una cadena compleja donde los Cn(X) representan las "piezas" de esa forma. La homología de esta cadena te dice cuántos "agujeros" tiene la forma.
- Si tienes un complejo simplicial K (una forma construida con puntos, líneas, triángulos, etc.), los Cn(K) pueden ser las combinaciones de sus "piezas" de dimensión n.
En resumen, el álgebra homológica nos enseña que las cadenas complejas asociadas a objetos matemáticos (como formas o estructuras algebraicas) contienen mucha información valiosa. La homología es solo una parte de esa información, pero es muy útil para entender las propiedades de esos objetos.
Esta rama de las matemáticas nos da herramientas para:
- Estudiar cómo se relacionan las cadenas complejas y su homología cuando hay un mapa entre dos objetos. Por ejemplo, si estiras o doblas una forma, ¿cómo cambian sus "agujeros"?
- Entender que, aunque un objeto pueda describirse de diferentes maneras, su homología (los "agujeros") suele ser la misma. Esto significa que la homología es un invariante del objeto, una característica que no cambia.
Herramientas estándar
Sucesiones exactas
Una sucesión exacta es una cadena de grupos y mapas donde la "salida" de cada mapa es exactamente la "entrada" del siguiente.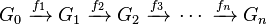 
Esto significa que la imagen de un mapa es igual al kernel (los elementos que se vuelven cero) del siguiente: 
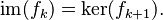Esta idea se usa también para otros tipos de estructuras, como espacios vectoriales o módulos.
Sucesión exacta corta
Un tipo muy común es la sucesión exacta corta, que tiene esta forma: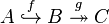 
Aquí, f es un mapa que "inyecta" A en B (como si A fuera una parte de B), y g es un mapa que "cubre" C (como si C fuera lo que queda de B después de quitar A). En este caso, C es como el resultado de dividir B por la parte que viene de A: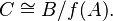 
Una sucesión exacta corta de grupos abelianos a menudo se escribe con ceros al principio y al final para indicar que no hay más elementos: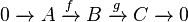 
El 0 representa un grupo trivial (que solo tiene un elemento).
Sucesión exacta larga
Una sucesión exacta larga es simplemente una sucesión exacta que puede extenderse infinitamente.
El lema de los cinco
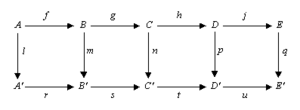
El lema de los cinco es una herramienta útil para demostrar que ciertos mapas son isomorfismos (es decir, que son "iguales" en un sentido matemático). Imagina un diagrama con dos filas de sucesiones exactas y cinco mapas verticales que las conectan:
Si las filas son exactas, y los mapas m y p son isomorfismos, y l es un epimorfismo (cubre todo), y q es un monomorfismo (inyecta sin perder información), entonces el lema dice que el mapa n también debe ser un isomorfismo. Es como si la información fluyera a través del diagrama y forzara a n a ser un isomorfismo.
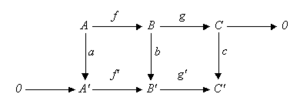
El lema de la serpiente
El lema de la serpiente es otra herramienta importante que relaciona los "agujeros" (kernels) y los "cocientes" (cokernels) en un diagrama conmutativo. Considera este diagrama:
Si las filas son sucesiones exactas, entonces existe una nueva sucesión exacta que conecta los kernels y cokernels de los mapas a, b y c: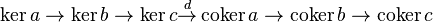 
Este lema es muy útil para construir sucesiones exactas largas a partir de sucesiones exactas cortas.
Categorías abelianas
En matemáticas, una categoría abeliana es un tipo especial de categoría donde se pueden sumar los morfismos (los mapas entre objetos) y donde existen los kernels y cokernels (conceptos relacionados con los "agujeros" y "cocientes"). Además, tienen propiedades muy "estables".
El ejemplo más sencillo de una categoría abeliana es la categoría de grupos abelianos, que se llama Ab. La teoría de categorías abelianas fue desarrollada por Alexander Grothendieck para unificar diferentes teorías de homología.
Para que una categoría sea abeliana, debe cumplir varias condiciones:
- Debe tener un objeto nulo (como el grupo que solo tiene el cero).
- Debe tener todos los productos y coproductos (formas de combinar objetos).
- Debe tener todos los kernels y cokernels.
- Todos sus monomorfismos (mapas que inyectan) y epimorfismos (mapas que cubren) deben ser "normales".
Estas propiedades hacen que las categorías abelianas sean fundamentales en el álgebra homológica y en otras áreas como la geometría algebraica.
El functor Ext
El functor Ext es una herramienta avanzada en álgebra homológica que ayuda a medir "cuánto" un módulo (un tipo de estructura algebraica) no es "libre" o "proyectivo". Se calcula usando cadenas complejas especiales llamadas "resoluciones".
Existen dos formas de calcularlo, y ambas dan el mismo resultado. Una forma es usando una "resolución inyectiva" y la otra es usando una "resolución proyectiva". Ambas involucran construir una cadena compleja y luego calcular su homología.
Funtorialidad
Un mapa continuo entre dos espacios topológicos (como estirar o doblar una forma) produce un homomorfismo (un mapa que conserva la estructura) entre sus grupos de homología. Esto significa que si dos formas están relacionadas, sus "agujeros" también lo están de una manera compatible.
En álgebra homológica, esto se explica a través de los morfismos entre cadenas complejas. Un morfismo entre dos cadenas complejas es una familia de mapas que "conmutan" con los diferenciales (es decir, el orden en que aplicas los mapas no importa).
Un morfismo de cadenas complejas induce un morfismo entre sus grupos de homología. Si este morfismo induce un isomorfismo en la homología, se le llama cuasi-isomorfismo.
Muchas construcciones de cadenas complejas tienen la propiedad de functorialidad. Esto significa que si tienes un mapa entre dos objetos X e Y, entonces también hay un mapa compatible entre sus cadenas complejas. Y si combinas mapas, los mapas de las cadenas complejas también se combinan de la misma manera. Esto asegura que los grupos de homología también son functoriales, lo que significa que los mapas entre objetos matemáticos dan lugar a mapas compatibles entre sus "agujeros".
Una situación común es un triple exacto o una secuencia exacta corta de complejos. Esto ocurre cuando tienes tres cadenas complejas conectadas por dos morfismos, formando una sucesión exacta en cada nivel: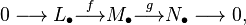 
Esto significa que para cada n, la secuencia de grupos individuales es exacta: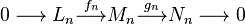 
Véase también
En inglés: Homological algebra Facts for Kids
