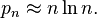Teorema de los números primos para niños
El teorema de los números primos es una idea muy importante en las matemáticas que nos ayuda a entender cómo se distribuyen los números primos entre los números naturales. Los números primos son aquellos que solo se pueden dividir por 1 y por sí mismos (como 2, 3, 5, 7, etc.). Este teorema nos dice que, a medida que los números se hacen más grandes, los primos se vuelven menos comunes.
Este teorema es uno de los descubrimientos más significativos en la historia de las matemáticas. No solo es interesante por sí mismo, sino que también ha impulsado muchas investigaciones sobre los números primos.
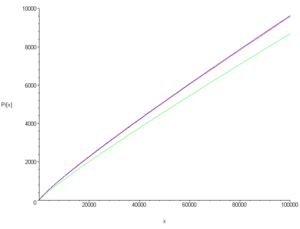
Una forma de entenderlo es con la función π ( N ), que cuenta cuántos números primos hay hasta un número N. El teorema dice que esta cantidad es muy parecida a dividir N entre el logaritmo natural de N (que se escribe ln( N )). Esto significa que, para números N muy grandes, la posibilidad de que un número elegido al azar hasta N sea primo es aproximadamente 1ln ( N ).
Por ejemplo, si tomas números de hasta 1000 dígitos, aproximadamente 1 de cada 2300 es primo. Pero si tomas números de hasta 2000 dígitos, aproximadamente 1 de cada 4600 es primo. Esto muestra que los números primos están más separados a medida que los números son más grandes.
Contenido
¿Cómo se expresa el teorema?
Imagina que 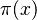 es una función que nos dice cuántos números primos hay que no son mayores que
es una función que nos dice cuántos números primos hay que no son mayores que 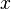 . El teorema de los números primos se expresa así:
. El teorema de los números primos se expresa así:
|
Esto no significa que la diferencia entre 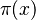 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x}{\ln(x)} sea cero para números muy grandes. Lo que significa es que, si dividimos
y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x}{\ln(x)} sea cero para números muy grandes. Lo que significa es que, si dividimos 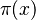 entre Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x}{\ln(x)} , el resultado se acerca mucho a 1 a medida que
entre Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x}{\ln(x)} , el resultado se acerca mucho a 1 a medida que  se hace muy grande.
se hace muy grande.
Hay otra aproximación aún mejor que usa algo llamado la integral logarítmica:
|
Historia del descubrimiento
La idea de este teorema surgió hace mucho tiempo.
Primeras conjeturas
En 1792 o 1793, un joven matemático llamado Carl Friedrich Gauss, que tenía solo 15 o 16 años, anotó en su cuaderno una observación clave. Él pensó que la cantidad de números primos menores que un número a (que él imaginó como infinito) se acercaba a a dividido por el logaritmo de a. Esta es considerada la primera vez que se planteó la idea del teorema de los números primos. Gauss también fue quien definió la función 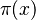 para contar los primos.
para contar los primos.
Otro matemático, Adrien-Marie Legendre, también hizo una conjetura similar en 1798. Él sugirió una fórmula para 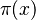 que se parecía a la de Gauss. Más tarde, en 1808, Legendre hizo su conjetura más precisa.
que se parecía a la de Gauss. Más tarde, en 1808, Legendre hizo su conjetura más precisa.
Otros matemáticos importantes como Peter Gustav Lejeune Dirichlet, Pafnuty Chebyshev y Bernhard Riemann también hicieron contribuciones significativas a esta idea.
La demostración formal
La demostración completa y formal del teorema fue lograda de forma independiente por dos matemáticos, Jacques Hadamard y Charles-Jean de la Vallée Poussin, en el año 1896. Sus demostraciones usaron métodos avanzados de las matemáticas.
Desde entonces, la forma de expresar el teorema se ha ido mejorando. En 1912, J. E. Littlewood demostró algo sorprendente: aunque por lo general la aproximación Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{Li}(x) es mayor que 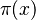 , hay momentos en que
, hay momentos en que 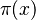 la supera para números muy grandes.
la supera para números muy grandes.
Pruebas más sencillas
Las demostraciones originales de Hadamard y de la Vallée Poussin eran bastante complicadas. Sin embargo, a lo largo del siglo XX, se encontraron pruebas más sencillas. En 1949, Atle Selberg y Paul Erdős encontraron pruebas que no necesitaban herramientas matemáticas tan avanzadas. Más tarde, en 1980, el matemático estadounidense Donald J. Newman descubrió una prueba aún más simple.
Relación con la hipótesis de Riemann
El teorema de los números primos está muy relacionado con una de las preguntas más famosas y sin resolver en matemáticas: la hipótesis de Riemann. Esta hipótesis trata sobre la función zeta de Riemann, que es una herramienta matemática muy importante para estudiar los números primos.
Si la hipótesis de Riemann fuera cierta, entonces podríamos hacer que la aproximación del teorema de los números primos fuera aún más precisa. En 1901, Helge von Koch demostró que si la hipótesis de Riemann es verdadera, el error en la aproximación del teorema de los números primos sería lo más pequeño posible.
Aproximación para el enésimo número primo
Gracias al teorema de los números primos, también podemos estimar el valor del enésimo número primo. Si queremos saber cuál es el primo número 100, o el 1000, o el que sea, podemos usar una fórmula aproximada.
Si llamamos 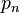 al enésimo número primo (por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p_1=2 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p_2=3 , etc.), entonces:
al enésimo número primo (por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p_1=2 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p_2=3 , etc.), entonces:
Esto significa que el enésimo número primo es aproximadamente igual a n multiplicado por el logaritmo natural de n.
Teorema de los números primos para progresiones aritméticas
Los números primos no solo se distribuyen en general, sino también dentro de grupos especiales de números llamados progresiones aritméticas. Una progresión aritmética es una secuencia de números donde la diferencia entre cada número y el siguiente es siempre la misma (por ejemplo, 1, 5, 9, 13... donde la diferencia es 4).
Matemáticos como Dirichlet y Legendre conjeturaron, y Vallée-Poussin demostró, que si los números de la progresión no tienen factores comunes, los números primos se distribuyen de manera uniforme entre ellos.
La "carrera de números primos"
A veces, al estudiar cómo se distribuyen los primos en diferentes progresiones aritméticas, parece que una progresión tiene más primos que otra. Esto se conoce como la "carrera de números primos". Por ejemplo, los primos que terminan en 3 (como 3, 13, 23...) suelen ser más numerosos que los que terminan en 1 (como 11, 31, 41...) en los primeros números.
Sin embargo, en 1914, Littlewood demostró que, aunque una progresión pueda ir "ganando" al principio, la "carrera" cambia de líder infinitas veces. Es decir, la ventaja de una progresión sobre otra se invierte una y otra vez a medida que los números se hacen más grandes.
Véase también
 En inglés: Prime number theorem Facts for Kids
En inglés: Prime number theorem Facts for Kids


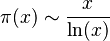 , donde
, donde 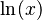 es el
es el 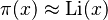 , donde
, donde 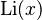 es la integral logarítmica desplazada de
es la integral logarítmica desplazada de