Raíz cuadrada para niños
En matemáticas, la raíz cuadrada de un número es otro número que, al multiplicarse por sí mismo, nos da el número original. Por ejemplo, la raíz cuadrada de 9 es 3, porque 3 multiplicado por 3 es igual a 9. Se escribe con un símbolo especial llamado "radical" (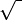 ).
).
Cuando calculamos la raíz cuadrada de un número positivo, siempre hay dos resultados posibles: uno positivo y uno negativo. Por ejemplo, la raíz cuadrada de 25 es 5, pero también es -5, porque 5x5=25 y (-5)x(-5)=25. Sin embargo, cuando usamos el símbolo 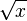 , nos referimos a la raíz cuadrada positiva, que se llama "raíz cuadrada principal".
, nos referimos a la raíz cuadrada positiva, que se llama "raíz cuadrada principal".
Contenido
¿Cómo se descubrieron las raíces cuadradas?
Las raíces cuadradas son muy antiguas. Surgieron cuando la gente intentaba resolver problemas de geometría, como calcular la longitud de la diagonal de un cuadrado.
Raíces cuadradas en la antigüedad
Los antiguos egipcios ya sabían cómo calcular raíces cuadradas. Hay un documento muy antiguo llamado el Papiro de Ahmes, de hace unos 3600 años, que lo demuestra.
En la antigua India, también se conocían las raíces cuadradas. Textos de hace más de 2000 años, como los Sulba Sutras, muestran métodos para encontrar aproximaciones de raíces cuadradas, como la de 2 o 3. Un matemático llamado Aryabhata, que vivió hace unos 1500 años, también describió un método para calcular raíces cuadradas de números grandes.
Los babilonios usaban un método para aproximar raíces cuadradas que se basaba en la media aritmética. Era como ir haciendo cálculos cada vez más precisos para acercarse al valor real.
El descubrimiento de los números irracionales
Durante el periodo griego antiguo, especialmente con los pitagóricos, se investigaron mucho las raíces cuadradas. Fue entonces cuando descubrieron algo sorprendente: la raíz cuadrada de 2 no se podía escribir como una fracción de dos números enteros. A estos números los llamaron "irracionales" o "inconmensurables". Este descubrimiento fue muy importante para las matemáticas de la época.
Al principio, las raíces cuadradas se usaban para resolver problemas de trigonometría y geometría, como el teorema de Pitágoras. Con el tiempo, se volvieron fundamentales para resolver ecuaciones de segundo grado y otras más complejas.
El símbolo de la raíz cuadrada
El símbolo que usamos hoy para la raíz cuadrada (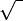 ) fue introducido en 1525 por el matemático Christoph Rudolff. Se cree que el signo es una forma estilizada de la letra "r" minúscula, que viene de la palabra latina radix, que significa "raíz".
) fue introducido en 1525 por el matemático Christoph Rudolff. Se cree que el signo es una forma estilizada de la letra "r" minúscula, que viene de la palabra latina radix, que significa "raíz".
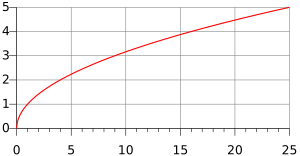
La función raíz cuadrada
La raíz cuadrada también puede verse como una función. Una función es como una máquina: le das un número y te devuelve otro. La función raíz cuadrada de x se escribe como 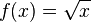 . Solo funciona con números positivos o cero.
. Solo funciona con números positivos o cero.
Cuando la raíz cuadrada de un número entero es un número entero, decimos que ese número es un cuadrado perfecto. Por ejemplo:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{16} = 4 , porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4 \times 4 = 16
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{64} = 8 , porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 8 \times 8 = 64
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{144} = 12 , porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 12 \times 12 = 12^2
Si un número entero no es un cuadrado perfecto, su raíz cuadrada es un número irracional. Esto significa que no se puede escribir como una fracción simple. Por ejemplo, 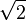 es un número irracional.
es un número irracional.
Propiedades importantes
Las raíces cuadradas tienen algunas propiedades útiles:
- La raíz cuadrada de un producto es el producto de las raíces cuadradas: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{xy} = \sqrt x \sqrt y
- La raíz cuadrada de una división es la división de las raíces cuadradas: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}
- La raíz cuadrada de un número al cuadrado es su valor absoluto: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{x^2} = |x| . Esto significa que si x es positivo, el resultado es x; si x es negativo, el resultado es -x (para que sea positivo).
¿Cómo se calculan las raíces cuadradas?
Hoy en día, usamos calculadoras o computadoras para encontrar raíces cuadradas, pero también hay métodos para hacerlas a mano.
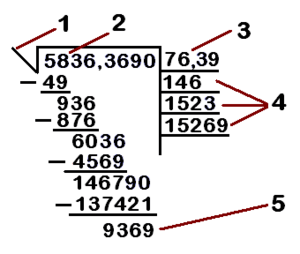
Partes de una raíz cuadrada
Cuando ves una operación de raíz cuadrada, tiene varias partes:
- Radical: Es el símbolo
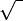 que indica la operación.
que indica la operación. - Radicando: Es el número dentro del radical, al que le queremos calcular la raíz cuadrada.
- Raíz: Es el resultado de la operación.
- Renglones auxiliares: Son los pasos intermedios que se usan en el cálculo manual.
- Resto: Es lo que sobra al final del cálculo, si la raíz no es exacta.
Cálculo con máquinas
Las calculadoras y los programas de computadora calculan las raíces cuadradas usando fórmulas matemáticas más avanzadas, a menudo relacionadas con las funciones exponenciales y los logaritmos.
Construcción geométrica de la raíz cuadrada
Podemos "dibujar" la raíz cuadrada de un número usando una regla y un compás. Esto es útil para entender cómo se relacionan las raíces cuadradas con la geometría.
Pasos para la construcción
1. Dibuja un segmento de línea 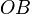 con la longitud del número al que quieres calcular la raíz cuadrada (llamémosle a). 2. Extiende ese segmento una unidad más, desde O hacia la izquierda, hasta un punto A. Así tendrás un segmento
con la longitud del número al que quieres calcular la raíz cuadrada (llamémosle a). 2. Extiende ese segmento una unidad más, desde O hacia la izquierda, hasta un punto A. Así tendrás un segmento 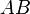 de longitud Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a + 1 . 3. Dibuja un círculo que tenga como diámetro el segmento
de longitud Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a + 1 . 3. Dibuja un círculo que tenga como diámetro el segmento 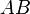 . 4. Desde el punto O (donde empieza la extensión de 1 unidad), traza una línea recta que sea perpendicular a
. 4. Desde el punto O (donde empieza la extensión de 1 unidad), traza una línea recta que sea perpendicular a 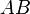 . Esta línea cortará el círculo en un punto (llamémosle H). 5. La longitud del segmento
. Esta línea cortará el círculo en un punto (llamémosle H). 5. La longitud del segmento 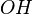 será exactamente la raíz cuadrada de a (
será exactamente la raíz cuadrada de a (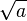 ).
).
Esta construcción demuestra visualmente que la raíz cuadrada de un número se puede representar como una longitud.
Raíces cuadradas especiales
Raíz cuadrada de 2 (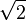 )
)
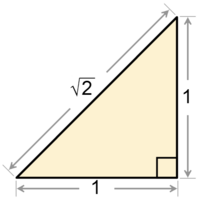
La raíz cuadrada de 2 es aproximadamente 1.4142135623. Es famosa porque fue el primer número irracional descubierto, lo que causó un gran impacto en las matemáticas antiguas. Geométricamente, es la longitud de la diagonal de un cuadrado cuyos lados miden 1.
Raíz cuadrada de 3 (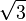 )
)
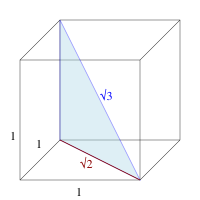
La raíz cuadrada de 3 es aproximadamente 1.7320508075. También se conoce como la constante de Teodoro. Es la longitud de la diagonal de un cubo cuyas aristas miden 1.
Raíz cuadrada de 5 (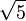 )
)
La raíz cuadrada de 5 es aproximadamente 2.2360679774. Aparece en la fórmula del número áureo, un número muy especial que se encuentra en la naturaleza y el arte. Geométricamente, es la hipotenusa de un triángulo rectángulo con catetos de longitud 1 y 2.
¿Para qué se usan las raíces cuadradas?
Las raíces cuadradas se usan en muchos campos:
- Para calcular la longitud de los lados de un triángulo rectángulo usando el teorema de Pitágoras.
- Para encontrar el radio de un círculo si conocemos su área.
- Para saber si un número es primo: solo necesitas revisar si es divisible por números primos menores que su raíz cuadrada.
- En física, para calcular el tiempo en movimientos acelerados.
- En álgebra, para resolver ecuaciones de segundo grado.
- Para calcular la diagonal de un cuadrado si conocemos su área.
- En trigonometría, para definir los valores de seno y coseno de algunos ángulos.
Galería de imágenes
Véase también
 En inglés: Square root Facts for Kids
En inglés: Square root Facts for Kids


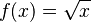 es una semi
es una semi