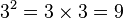robot de la enciclopedia para niños

Cuadrado perfecto para niños

Enciclopedia para niños

Un cuadrado perfecto es un número entero que se obtiene al multiplicar otro número entero por sí mismo. Por ejemplo, 9 es un cuadrado perfecto porque es el resultado de multiplicar 3 por 3 (3 × 3 = 9). También se le llama número cuadrado.

Imagina que tienes un grupo de objetos y puedes organizarlos formando un cuadrado perfecto. Si tienes 9 objetos, puedes hacer un cuadrado de 3 filas y 3 columnas.

32 = 9 Square number 9.png

En álgebra, cuando elevamos un número n al cuadrado, lo escribimos como n². Esto significa n multiplicado por n. Esta operación nos ayuda a calcular el área de un cuadrado si conocemos la medida de uno de sus lados. Por eso se le llama "elevar al cuadrado".

Archivo:SquareProperties
Elevar 5 al cuadrado nos da el área de un cuadrado de lado 5.

Un número natural n elevado al cuadrado también se puede obtener sumando los primeros números impares. Por ejemplo:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3^2 = 1 + 3 + 5 = 9

Esto es lo mismo que:

3^2 = 3\times 3=9

¿Qué son los números cuadrados?

Los números cuadrados son aquellos que resultan de multiplicar un número entero por sí mismo. Son muy importantes en matemáticas y los encontramos en muchas situaciones.

Propiedades de los números cuadrados

Los números cuadrados tienen algunas características interesantes:

  • El n-ésimo número cuadrado (el que se obtiene al elevar n al cuadrado) es igual a la suma de los primeros n números impares.

* Por ejemplo, para 52: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5^2 = 1 + 3 + 5 + 7 + 9 = 25

  • La cantidad de divisores (números que lo dividen exactamente) de un cuadrado perfecto siempre es un número impar. Si un número no es un cuadrado perfecto, la cantidad de sus divisores es par.

* Por ejemplo, los divisores de 9 son 1, 3, 9 (3 divisores, que es impar). * Los divisores de 12 son 1, 2, 3, 4, 6, 12 (6 divisores, que es par).

¿Cómo terminan los números cuadrados?

El último dígito de un número cuadrado perfecto nos da pistas sobre el número original:

  • Si un número termina en 0, su cuadrado termina en 00. Por ejemplo, 302 = 900.
  • Si un número termina en 1 o 9, su cuadrado termina en 1. Por ejemplo, 212 = 441, 292 = 841.
  • Si un número termina en 2 u 8, su cuadrado termina en 4. Por ejemplo, 722 = 5184, 782 = 6084.
  • Si un número termina en 3 o 7, su cuadrado termina en 9. Por ejemplo, 532 = 2809, 572 = 3249.
  • Si un número termina en 4 o 6, su cuadrado termina en 6. Por ejemplo, 442 = 1936, 462 = 2116.
  • Si un número termina en 5, su cuadrado termina en 25. Por ejemplo, 852 = 7225.
  • Por lo tanto, ningún cuadrado perfecto entero puede terminar en 2, 3, 7 ni 8.

Ejemplos de números cuadrados

Aquí tienes algunos de los primeros números cuadrados perfectos:

12 = 1 Square number 1.png
22 = 4 Square number 4.png
32 = 9 Square number 9.png
42 = 16 Square number 16.png
52 = 25 Square number 25.png

Los primeros 50 cuadrados perfectos son:

02 = 0 ((sucesión A000290 en OEIS))
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
112 = 121
122 = 144
132 = 169
142 = 196
152 = 225
162 = 256
172 = 289
182 = 324
192 = 361
202 = 400
212 = 441
222 = 484
232 = 529
242 = 576
252 = 625
262 = 676
272 = 729
282 = 784
292 = 841
302 = 900
312 = 961
322 = 1024
332 = 1089
342 = 1156
352 = 1225
362 = 1296
372 = 1369
382 = 1444
392 = 1521
402 = 1600
412 = 1681
422 = 1764
432 = 1849
442 = 1936
452 = 2025
462 = 2116
472 = 2209
482 = 2304
492 = 2401
502 = 2500

¿Cómo calcular cuadrados cercanos?

Podemos calcular un cuadrado a partir de otro que ya conocemos.

Calcular el siguiente cuadrado

Para encontrar el siguiente cuadrado, puedes sumar al cuadrado actual el doble del lado del siguiente número, y luego restar 1.

  • Si 42 = 16, para 52: 16 + (2 * 5) - 1 = 16 + 10 - 1 = 25.

Otra forma de ver esto es que la diferencia entre cada número cuadrado y el siguiente son los números impares en orden ascendente:

  • 0 + 1 = 1 (12)
  • 1 + 3 = 4 (22)
  • 4 + 5 = 9 (32)
  • 9 + 7 = 16 (42)
  • 16 + 9 = 25 (52)

Calcular el cuadrado dos posiciones más adelante

Para encontrar un cuadrado que está dos posiciones más adelante, puedes sumar al cuadrado actual 4 veces el (lado deseado - 1).

  • Si 42 = 16, para 62: 16 + (4 * (6-1)) = 16 + (4 * 5) = 16 + 20 = 36.

Calcular el cuadrado anterior

Para encontrar el cuadrado anterior, puedes restar al cuadrado actual el doble del lado actual, y luego sumar 1.

  • Si 62 = 36, para 52: 36 - (2 * 6) + 1 = 36 - 12 + 1 = 25.

Calcular el cuadrado dos posiciones atrás

Para encontrar un cuadrado que está dos posiciones atrás, puedes restar al cuadrado actual 4 veces el (lado actual - 1).

  • Si 62 = 36, para 42: 36 - (4 * (6-1)) = 36 - (4 * 5) = 36 - 20 = 16.

Cuadrados como sumas especiales

El cuadrado de cualquier número también se puede representar como una suma de números repetidos. Por ejemplo, el cuadrado de 4 (42) es igual a:

  • 1 + 1 + 2 + 2 + 3 + 3 + 4 = 16.

Esto es útil para calcular cuadrados de números grandes. Por ejemplo, para 522:

  • 522 = 502 + 50 + 51 + 51 + 52 = 2500 + 204 = 2704.

Un número cuadrado también puede ser la suma de dos números triangulares consecutivos. Un número triangular es el resultado de sumar números consecutivos (1, 1+2=3, 1+2+3=6, etc.).

Cuadrados de números pares e impares

  • El cuadrado de un número par siempre es un número par. De hecho, siempre es divisible por 4.

* Por ejemplo, (2 × 3)2 = 62 = 36, y 36 es par y divisible por 4.

  • El cuadrado de un número impar siempre es un número impar.

* Por ejemplo, (2 × 3 + 1)2 = 72 = 49, y 49 es impar.

Esto significa que si un cuadrado perfecto es par, su raíz cuadrada (el número original) también será par. Y si un cuadrado perfecto es impar, su raíz cuadrada también será impar.

Suma de los primeros n cuadrados

Si quieres sumar los primeros n números cuadrados perfectos, puedes usar una fórmula especial. Para los primeros cinco cuadrados perfectos (12 + 22 + 32 + 42 + 52):

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 + 4 + 9+ 16+25 =\frac{5(5+1)(2\times5+1)}{6} = \frac{5 \times 6 \times 11}{6} = 5 \times 11 = 55

En general, la suma de los primeros n cuadrados perfectos es:

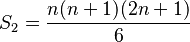
S_2 = \frac{n(n+1)(2n+1)}{6}

¿Cómo se forman los cuadrados perfectos?

Hay algunas formas interesantes de "construir" cuadrados perfectos:

  • Si multiplicas dos números pares consecutivos y le sumas 1, el resultado es un cuadrado perfecto.

* Por ejemplo, 52 × 54 + 1 = 2808 + 1 = 2809, que es el cuadrado de 53.

  • Si multiplicas dos números impares consecutivos y le sumas 1, el resultado es un cuadrado perfecto.

* Por ejemplo, 95 × 97 + 1 = 9215 + 1 = 9216, que es el cuadrado de 96.

  • Si multiplicas cuatro números enteros consecutivos y le sumas 1, el resultado es un cuadrado perfecto.

* Por ejemplo, 13 × 14 × 15 × 16 + 1 = 43680 + 1 = 43681, que es el cuadrado de 209.

Galería de imágenes

  • Square number 9

    Un cuadrado de 3 por 3.

  • SquareProperties

    El área de un cuadrado de lado 5 es 5 al cuadrado.

  • Square number 1

    Un cuadrado de 1 por 1.

  • Square number 4

    Un cuadrado de 2 por 2.

  • Square number 16

    Un cuadrado de 4 por 4.

  • Square number 25

    Un cuadrado de 5 por 5.

Véase también

Kids robot.svg En inglés: Square number Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Cuadrado_perfecto&oldid=4937663»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Cuadrado perfecto para Niños. Enciclopedia Kiddle.