Triángulo rectángulo para niños
En geometría, un triángulo rectángulo es un tipo especial de triángulo que tiene un ángulo recto, es decir, un ángulo que mide exactamente 90 grados. Las relaciones entre las longitudes de los lados de un triángulo rectángulo son muy importantes en la trigonometría, una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Una de las propiedades más famosas de estos triángulos es el teorema de Pitágoras, que ya era conocido por civilizaciones antiguas como los babilonios hace miles de años.
Contenido
¿Qué es un Triángulo Rectángulo?
Lados y Ángulos Clave
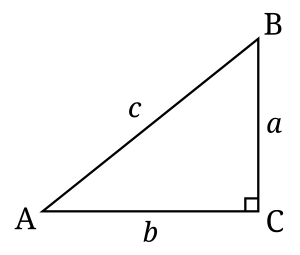
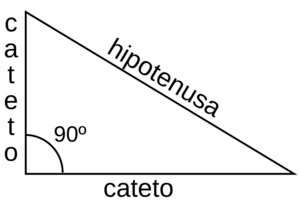
En un triángulo rectángulo, los lados tienen nombres especiales:
- La hipotenusa es el lado más largo del triángulo y siempre está enfrente del ángulo recto.
- Los catetos son los dos lados más cortos que forman el ángulo recto. Cada cateto está enfrente de uno de los otros dos ángulos, que siempre son agudos (miden menos de 90 grados).
Propiedades Importantes del Triángulo Rectángulo
Los triángulos rectángulos tienen características únicas:
- Siempre tienen un ángulo de 90 grados.
- Los otros dos ángulos son agudos y, si los sumas, siempre dan 90 grados. Se dice que son ángulos complementarios.
- La hipotenusa siempre es más larga que cualquiera de los catetos.
- El área de un triángulo rectángulo se puede calcular fácilmente multiplicando la longitud de los dos catetos y dividiendo el resultado entre dos. Esto es porque un cateto puede ser la base y el otro la altura.
- La línea que va desde el ángulo recto hasta el punto medio de la hipotenusa (llamada mediana) mide exactamente la mitad de la hipotenusa.
Tipos de Triángulos Rectángulos
Existen diferentes tipos de triángulos rectángulos, según la medida de sus lados y ángulos:
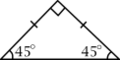
- Triángulo rectángulo isósceles: Este triángulo tiene dos catetos de la misma longitud. Esto significa que sus dos ángulos agudos también son iguales, midiendo 45 grados cada uno. Así, sus ángulos son 45-45-90. En este caso, la hipotenusa es aproximadamente 1.414 veces más larga que un cateto.
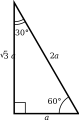
- Triángulo rectángulo escaleno: En este tipo, los tres lados tienen longitudes diferentes y, por lo tanto, los tres ángulos también son diferentes. Un ejemplo muy conocido es el triángulo con ángulos de 30-60-90 grados. En estos triángulos, la hipotenusa mide el doble que el cateto más corto, y el cateto más largo es aproximadamente 1.732 veces la longitud del cateto más corto.
- Triángulo rectángulo con lados consecutivos: Un ejemplo famoso es el triángulo con lados que miden 3, 4 y 5 unidades. Este triángulo fue muy usado en civilizaciones antiguas como Babilonia y Egipto. Otro ejemplo es el triángulo con lados de 5, 12 y 13 unidades.
El Famoso Teorema de Pitágoras
El teorema de Pitágoras es una regla fundamental para los triángulos rectángulos. Dice que:
En cualquier triángulo rectángulo, si elevas al cuadrado la longitud de la hipotenusa, el resultado será igual a la suma de los cuadrados de las longitudes de los dos catetos.
Esto se puede escribir con una fórmula: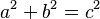 
Donde:
- a y b son las longitudes de los catetos.
- c es la longitud de la hipotenusa.
Si conoces dos lados de un triángulo rectángulo, puedes usar esta fórmula para encontrar el lado que falta:
- Para encontrar la hipotenusa (c): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c = \sqrt{a^2 + b^2}
- Para encontrar un cateto (a): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a = \sqrt{c^2 - b^2}
- Para encontrar el otro cateto (b): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b = \sqrt{c^2 - a^2}
Relaciones Métricas en el Triángulo Rectángulo
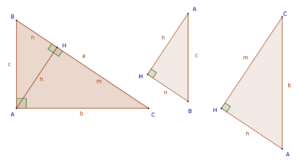
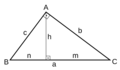
Cuando dibujamos una altura desde el ángulo recto hasta la hipotenusa, se forman otros dos triángulos rectángulos más pequeños. Estos tres triángulos (el original y los dos nuevos) son "semejantes", lo que significa que tienen la misma forma, aunque sean de diferente tamaño. Esto nos permite establecer algunas relaciones interesantes:
- Teorema de la altura: La altura (h) que va desde el ángulo recto hasta la hipotenusa es la media geométrica de las dos partes en que divide a la hipotenusa (m y n). Esto se expresa como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h^2 = m \cdot n o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h = \sqrt{m \cdot n} . También se puede calcular como el producto de los catetos dividido por la hipotenusa: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h = \frac{b \cdot c}{a} .
- Teorema del cateto: El cuadrado de la longitud de un cateto es igual al producto de la hipotenusa por la "proyección" de ese cateto sobre la hipotenusa. La proyección es la sombra que el cateto haría sobre la hipotenusa si la luz viniera perpendicularmente.
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b^2 = a \cdot m (para el cateto b y su proyección m) * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c^2 = a \cdot n (para el cateto c y su proyección n)
Razones Trigonométricas en Triángulos Rectángulos
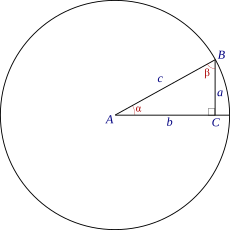
Las razones trigonométricas son relaciones entre los lados y los ángulos de un triángulo rectángulo. Son muy útiles para calcular medidas desconocidas. Para un ángulo agudo (llamémoslo alfa, 
):
- El seno de un ángulo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \text{sen}(\alpha) ) es la división entre la longitud del cateto opuesto a ese ángulo y la longitud de la hipotenusa.
- El coseno de un ángulo (
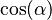) es la división entre la longitud del cateto adyacente (el que está al lado) a ese ángulo y la longitud de la hipotenusa. - La tangente de un ángulo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tan(\alpha) ) es la división entre la longitud del cateto opuesto y la longitud del cateto adyacente.
También existen las razones inversas: la cosecante (inverso del seno), la secante (inverso del coseno) y la cotangente (inverso de la tangente).
Área de un Triángulo Rectángulo
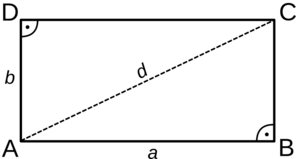
Calcular el área de un triángulo rectángulo es muy sencillo. Imagina que tienes un rectángulo y lo cortas por la mitad con una línea diagonal. Cada una de esas mitades es un triángulo rectángulo.
Por eso, el área de un triángulo rectángulo es la mitad del área de un rectángulo. La fórmula es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{\text{cateto1} \cdot \text{cateto2}}{2}
Donde "cateto1" y "cateto2" son las longitudes de los dos catetos. Esto funciona porque en un triángulo rectángulo, un cateto puede ser la base y el otro cateto puede ser la altura.
Triángulos Rectángulos en 3D
Si haces girar un triángulo rectángulo alrededor de uno de sus catetos, la figura que se forma es un cono. El cateto que no gira se convierte en el radio de la base del cono, y el cateto alrededor del cual gira se convierte en la altura del cono. La hipotenusa, al girar, forma la superficie curva del cono.
Galería de imágenes
-
Triángulo rectángulo isósceles.
-
Triángulo rectángulo escaleno.
-
Figura 1: Teorema de la altura y del cateto.
Véase también
En inglés: Right triangle Facts for Kids
- Teorema de Pitágoras
- Triángulo
- Cateto
- Hipotenusa
- Teorema de la altura
