Puntos de Lagrange para niños
Los puntos de Lagrange, también conocidos como puntos L o puntos de libración, son lugares especiales en el espacio. Imagina un sistema donde dos objetos grandes, como el Sol y la Tierra, giran uno alrededor del otro. Los puntos de Lagrange son cinco posiciones donde un objeto más pequeño, como un satélite artificial, puede permanecer quieto en relación con esos dos objetos grandes.
En estos puntos, la fuerza de gravedad combinada de los dos objetos grandes y la fuerza centrífuga (la que te empuja hacia afuera cuando giras) se equilibran perfectamente. Esto permite que el objeto pequeño se quede en una posición "fija" en el espacio, en lugar de moverse constantemente.
Para entenderlo mejor, piensa en un sistema de referencia que gira junto con los dos cuerpos grandes. Desde ese punto de vista, el objeto pequeño en un punto de Lagrange parece estar inmóvil.
Contenido
Descubrimiento y conceptos clave
Los primeros tres puntos de Lagrange (L1, L2, L3) fueron identificados por el científico Leonhard Euler alrededor de 1750. Unos diez años después, en 1772, el matemático Joseph-Louis Lagrange descubrió los dos puntos restantes.
Lagrange estaba estudiando el "problema de los tres cuerpos", que es muy complejo. Se trata de calcular cómo interactúan gravitacionalmente tres objetos en el espacio. Si solo hay dos cuerpos, es más sencillo predecir su movimiento. Pero al añadir un tercero, los cálculos se vuelven muy difíciles.
Lagrange simplificó el problema al suponer que un tercer cuerpo tenía una masa muy pequeña en comparación con los otros dos. Así, encontró cinco puntos específicos donde este tercer cuerpo, al seguir la órbita de los cuerpos más grandes, no sentiría ninguna fuerza neta. Estos lugares fueron nombrados puntos de Lagrange en su honor.
En el caso de órbitas que no son perfectamente circulares, los puntos de Lagrange no son lugares fijos, sino más bien "áreas" donde el equilibrio se mantiene.
¿Por qué las leyes de Kepler no son suficientes?
Las leyes de Kepler nos ayudan a entender cómo dos cuerpos orbitan entre sí. Por ejemplo, la tercera ley dice que cuanto más lejos está un planeta del Sol, más tiempo tarda en dar una vuelta completa. Esto significa que dos objetos a diferentes distancias del Sol nunca se moverán de forma sincronizada.
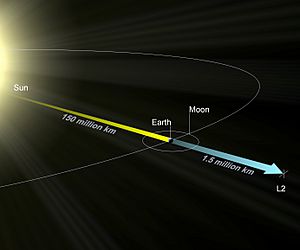
Sin embargo, cuando añadimos un tercer cuerpo, como un satélite artificial, las cosas se complican. Por ejemplo, un satélite entre el Sol y la Tierra debería tener un período orbital más corto que la Tierra. Pero si está en el punto L1 (a unos 1.5 millones de kilómetros de la Tierra), la atracción de la Tierra reduce la fuerza del Sol, y el satélite puede tener el mismo período orbital que la Tierra. Esto demuestra que la distancia no siempre significa un período más corto cuando hay más cuerpos interactuando.
Los cinco puntos de Lagrange
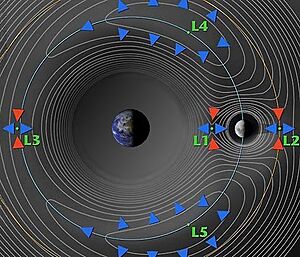
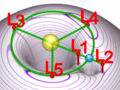
Existen cinco puntos de Lagrange, y cada uno tiene características especiales:
El punto L1: Observando el Sol
El punto L1 se encuentra en la línea que une los dos objetos grandes, justo entre ellos. En este punto, las fuerzas de gravedad de ambos cuerpos se anulan mutuamente.
- Ejemplo: Un objeto que orbita el Sol más cerca que la Tierra normalmente se movería más rápido. Pero si está en L1, la gravedad de la Tierra lo frena, haciendo que su velocidad y período orbital sean iguales a los de la Tierra. Este punto está a unos 1.5 millones de kilómetros de la Tierra.
El punto L1 del sistema Sol-Tierra es excelente para observar el Sol, ya que los objetos allí nunca son bloqueados por la Tierra o la Luna. La sonda espacial SOHO (Observatorio Solar y Heliosférico) está estacionada en L1.
El punto L2: Mirando el universo
El punto L2 también está en la línea que une los dos objetos grandes, pero más allá del más pequeño de ellos. Aquí, la gravedad de los dos cuerpos se combina para compensar la fuerza centrífuga.
- Ejemplo: Un objeto que orbita el Sol más lejos que la Tierra normalmente se movería más lento. Pero en L2, la gravedad adicional de la Tierra lo acelera, haciendo que su velocidad y período orbital sean iguales a los de la Tierra.
El punto L2 del sistema Sol-Tierra es ideal para los observatorios espaciales. Un objeto en L2 mantiene la misma orientación con respecto al Sol y la Tierra, lo que facilita su funcionamiento. El telescopio espacial James Webb se encuentra en el punto L2 del sistema Sol-Tierra.
El punto L3: El lado opuesto
El punto L3 se encuentra en la línea que une los dos objetos grandes, pero al otro lado del objeto más grande.
- Ejemplo: En el sistema Sol-Tierra, L3 está al lado opuesto del Sol, un poco más cerca del Sol que la Tierra. La gravedad combinada del Sol y la Tierra hace que un objeto en L3 orbite con el mismo período que la Tierra. En el pasado, algunos libros de ciencia ficción imaginaban una "Contra-Tierra" en L3, pero las observaciones han demostrado que no existe. L3 es un punto muy inestable debido a la influencia de otros planetas.
Los puntos L4 y L5: Los "troyanos"
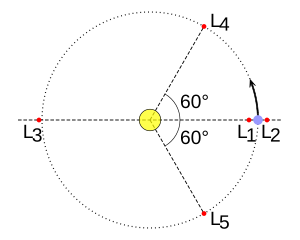
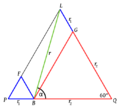
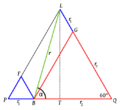
Los puntos L4 y L5 forman triángulos equiláteros con los dos objetos grandes. L4 está 60 grados por delante del objeto más pequeño en su órbita, y L5 está 60 grados por detrás. Estos puntos, junto con el objeto más pequeño, giran alrededor del centro de masa común de los dos cuerpos grandes.
La razón por la que estos puntos son estables es que L4 y L5 están a la misma distancia de los dos objetos grandes. Las fuerzas de gravedad se equilibran de tal manera que el objeto pequeño se mantiene en equilibrio con el resto del sistema.
L4 y L5 a veces se llaman "puntos troyanos". Este nombre viene de los asteroides troyanos del sistema Sol-Júpiter, que fueron nombrados como personajes de la Ilíada, la famosa historia de la guerra de Troya.
- Ejemplos:
* Los puntos L4 y L5 del sistema Sol-Tierra contienen principalmente polvo espacial y un asteroide troyano terrestre llamado 2010 TK7. * Los puntos L4 y L5 del sistema Tierra-Luna contienen nubes de polvo llamadas nubes de Kordylewski. * Los puntos L4 y L5 del sistema Sol-Júpiter están llenos de miles de asteroides troyanos. * Algunas lunas de Saturno, como Tetis y Dione, tienen lunas más pequeñas en sus puntos L4 y L5. Por ejemplo, Telesto y Calipso acompañan a Tetis. * La hipótesis del gran impacto sugiere que un objeto llamado Theia se formó en L4 o L5 y luego chocó con la Tierra, lo que pudo haber dado origen a la Luna.
Estabilidad de los puntos de Lagrange
Los puntos L1, L2 y L3 son inestables. Esto significa que si un objeto se desvía un poco de estos puntos, las fuerzas gravitatorias lo empujarán aún más lejos. Sin embargo, es posible mantener objetos en órbitas especiales alrededor de estos puntos, llamadas órbitas de "halo" o "Lissajous". Estas órbitas no son perfectamente estables, pero requieren poco esfuerzo para mantener una nave espacial en ellas durante mucho tiempo.
Los puntos L4 y L5, en cambio, son estables. Si un objeto en estos puntos se desvía un poco, una fuerza llamada efecto Coriolis lo empuja de vuelta al punto. Esto es cierto siempre que la masa del objeto más grande sea al menos 24.96 veces mayor que la del segundo objeto. Esto se cumple para los sistemas Sol-Tierra y Tierra-Luna.
Misiones espaciales en puntos de libración
Las características únicas de los puntos de Lagrange los hacen ideales para ciertas misiones espaciales. La NASA y la ESA (Agencia Espacial Europea) han enviado varias naves a los puntos L1 y L2 del sistema Sol-Tierra:
| Misión | Punto de Libración |
|---|---|
| GRAIL (Gravity Recovery and Interior Laboratory) |
L1
|
| Advanced Composition Explorer (ACE) |
L1
|
| Deep Space Climate Observatory (DSCOVR) |
L1
|
| Génesis |
L1
|
| International Cometary Explorer (ISEE-3) |
L1
|
| Observatorio Solar Helioesférico (SOHO) |
L1
|
| Wilkinson Microwave Anisotropy Probe (WMAP) (NASA) |
L2
|
| Observatorio Planck (ESA) |
L2
|
| Telescopio espacial James Webb (NASA) |
L2
|
También se ha explorado la idea de establecer colonias espaciales en los puntos L4 o L5 del sistema Tierra-Luna.
Ejemplos naturales de puntos de Lagrange
Los puntos de Lagrange no solo son útiles para las misiones espaciales, sino que también se encuentran en la naturaleza:
- En el sistema Sol-Júpiter, hay miles de asteroides, conocidos como asteroides troyanos, que orbitan en los puntos L4 o L5.
- También se han encontrado objetos en los puntos de Lagrange de otros sistemas, como Sol-Saturno, Sol-Marte y Sol-Neptuno.
- El asteroide 2010 TK7 es un troyano del sistema Sol-Tierra, ubicado en el punto L4.
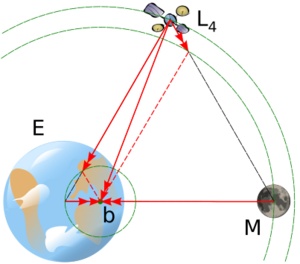
- Las nubes de Kordylewski, que son nubes de polvo, se han descubierto alrededor de los puntos L4 y L5 del sistema Tierra-Luna.
- La luna Tetis de Saturno tiene dos lunas más pequeñas, Telesto y Calipso, en sus puntos L4 y L5.
- La luna Dione de Saturno también tiene dos satélites, Helena y Pollux, en sus puntos L4 y L5.
Galería de imágenes
Véase también
 En inglés: Lagrange point Facts for Kids
En inglés: Lagrange point Facts for Kids
- Lista de objetos en los puntos de Lagrange
- Colonización de los puntos de Lagrange
- Problema de los dos cuerpos
- Problema de los tres cuerpos
- Esfera de Hill
- Nubes de Kordylewski
- Teoría del gran impacto