Problema de los dos cuerpos para niños
En mecánica, el problema de los dos cuerpos es un desafío para entender cómo se mueven dos objetos que solo interactúan entre sí. Imagina la Luna girando alrededor de la Tierra, o un planeta orbitando una estrella. También puede ser el caso de dos estrellas que giran una alrededor de la otra (una estrella binaria), o incluso un electrón alrededor de un núcleo atómico.
Las leyes de Newton nos permiten simplificar este problema. En lugar de estudiar dos objetos, podemos transformarlo en un problema de un solo objeto. Esto hace que sea mucho más fácil de resolver. Si uno de los objetos no es regular, la solución se vuelve muy difícil. A diferencia de este, el problema de los tres cuerpos (o más) es mucho más complejo y no tiene una solución exacta, salvo en casos muy específicos.
Contenido
¿Qué es el problema de los dos cuerpos?
Para entender el movimiento de dos objetos, como la Tierra y la Luna, necesitamos saber dónde están y qué tan rápido se mueven al principio. La segunda ley de Newton nos dice cómo las fuerzas afectan su movimiento.
Una forma inteligente de resolver este problema es dividirlo en dos partes más sencillas. Primero, vemos cómo se mueve el centro de masas de los dos objetos. Segundo, estudiamos cómo cambia la distancia y la dirección entre ellos. Al juntar estas dos soluciones, podemos saber exactamente cómo se mueve cada objeto.
El movimiento del centro de masas
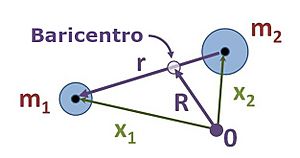
El centro de masas es como el punto de equilibrio de un sistema. Si sumamos las fuerzas que actúan sobre los dos objetos, y usamos la tercera ley de Newton (que dice que por cada acción hay una reacción igual y opuesta), descubrimos algo importante: el centro de masas de los dos objetos se mueve a una velocidad constante. Esto significa que la cantidad de movimiento total del sistema no cambia. Así, podemos predecir fácilmente dónde estará el centro de masas en cualquier momento.
El movimiento entre los objetos
Ahora, si restamos las ecuaciones de fuerza, podemos enfocarnos en cómo se mueve un objeto con respecto al otro. Para esto, usamos un concepto llamado masa reducida. Es como si tuviéramos un solo objeto con una masa especial que representa la interacción de los dos. La fuerza entre los objetos solo depende de la distancia entre ellos, no de su posición en el espacio. Esto es porque las leyes de la física son las mismas en todas partes.
Una vez que sabemos cómo se mueve el centro de masas y cómo se mueven los objetos entre sí, podemos calcular las trayectorias individuales de cada objeto.
Características del movimiento
El movimiento siempre es en un plano
El movimiento de dos objetos que interactúan siempre ocurre en un solo plano, como si estuvieran dibujando sus caminos en una hoja de papel. Esto se debe a que el momento angular del sistema se mantiene constante. El momento angular es una medida de cuánto "giro" tiene un sistema. Si el momento angular no cambia, significa que el movimiento no se sale de ese plano.
La ley de las áreas
A menudo, es útil usar coordenadas polares para describir el movimiento. Esto es porque la fuerza entre los objetos, como la gravedad, solo depende de la distancia entre ellos.
Cuando un objeto se mueve, el radio que lo une al otro objeto "barre" un área. La velocidad areolar es la rapidez con la que se barre esa área. Esta velocidad es constante. Esto significa que el objeto se mueve más rápido cuando está cerca del otro y más lento cuando está lejos.
Esta idea fue descubierta por Johannes Kepler en 1609 y es la segunda ley de Kepler, que explica cómo se mueven los planetas alrededor del Sol. Es una propiedad general de las fuerzas que actúan hacia un centro.
Para saber el ángulo de giro de un planeta con el tiempo, se usa una fórmula llamada ecuación de Kepler. Esta fórmula relaciona el tiempo con la posición del planeta en su órbita.
La forma de la órbita
Isaac Newton explicó que todos los objetos en el universo se atraen entre sí. Esta fuerza de gravitación depende de la masa de los objetos y de la distancia entre ellos. Cuanto más masivos son, más se atraen; cuanto más lejos están, menos se atraen.
Usando las leyes de Newton y un poco de matemáticas, se puede demostrar que la trayectoria que sigue un objeto alrededor de otro es una cónica. La forma exacta de esta trayectoria depende de un valor llamado excentricidad (e):
- Si e está entre 0 y 1, la órbita es una elipse (como la mayoría de los planetas).
- Si e es mayor que 1, la órbita es una hipérbola (el objeto se acerca y luego se aleja para siempre).
- Si e es igual a 1, la órbita es una parábola (el objeto también se acerca y se aleja para siempre, pero en un camino diferente).
Esto demuestra que la primera ley de Kepler, que dice que los planetas se mueven en elipses, es una consecuencia directa de la ley de la gravitación de Newton.
Importancia en la astronomía
El problema de los dos cuerpos es muy útil en la astronomía. Esto se debe a que muchos objetos celestes, como planetas y estrellas, se mueven rápidamente y están muy lejos de otros objetos. Esto significa que las influencias externas son pequeñas y pueden ignorarse.
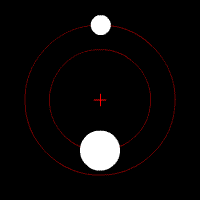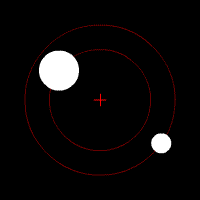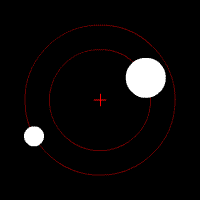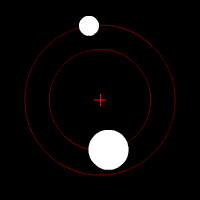
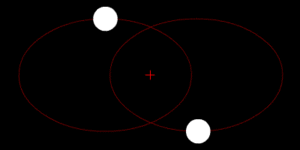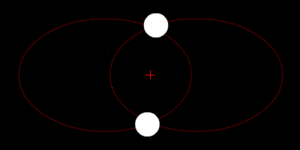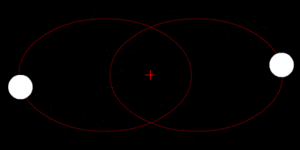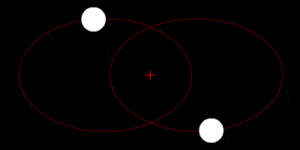
Bajo la fuerza de la gravedad, los objetos de un par orbitan alrededor de su centro de masas en forma de elipse. Si se mueven muy rápido, pueden escapar de la atracción mutua y seguir trayectorias de hipérbola o parábola. Si un objeto es mucho más pesado que el otro, el objeto más ligero se moverá mucho más alrededor del centro de masas compartido. El centro de masas incluso puede estar dentro del objeto más grande.
Este mismo tipo de solución se aplica a otros problemas donde las fuerzas siguen una ley similar, como la ley de Coulomb para la atracción eléctrica. Sin embargo, en la práctica, estos casos son menos comunes.
Extensiones y otros campos
Mecánica relativista
En la mecánica relativista, el problema de los dos cuerpos se vuelve más complejo. Esto es porque la interacción entre los cuerpos no es instantánea, sino que viaja a la velocidad de la luz. Además, en la teoría de la relatividad general, la gravedad cambia la forma del espacio-tiempo, lo que complica aún más el problema.
Mecánica cuántica
En la mecánica cuántica, el problema de dos cuerpos atraídos por fuerzas electromagnéticas sí tiene solución. Un ejemplo es el átomo hidrogenoide, que es como un átomo de hidrógeno. En este caso, el movimiento no es estrictamente plano. Por ejemplo, los electrónes alrededor de un núcleo atómico pueden encontrarse en cualquier plano que contenga al núcleo, a diferencia de los objetos grandes que siempre se mueven en un solo plano.
Ver también
- Leyes de Kepler
- Gravitación
- Problema de los tres cuerpos
- Problema de los n cuerpos
Véase también
 En inglés: Two-body problem Facts for Kids
En inglés: Two-body problem Facts for Kids