robot de la enciclopedia para niños

Ménsula para niños

Enciclopedia para niños
Archivo:Veruela - Claustro - Detalle 02
Ménsula en el Monasterio de Veruela, Provincia de Zaragoza, Aragón.
Archivo:Portada iglesia de Barajores de la Peña 003
Ejemplo de ménsula ambientada en el románico rural de la iglesia de Santa Bárbara en Barajores de la Peña (Palencia), Castilla y León.
Archivo:Aqueduct of Abánades (Canal of Castile in Osorno la Mayor) 013
Ménsula del acueducto de Abánades que permite el paso del canal de Castilla sobre el cauce del río Valdavia, Provincia de Burgos.

En arquitectura, una ménsula, palabra proveniente del latín mensula (mesa pequeña), es cualquier elemento estructural en voladizo. Se puede distinguir entre:

  • Ménsulas «cortas»: pequeños salientes que sirven de soporte para algún otro elemento, como el arranque de un arco, balcón o cubierta.
  • Ménsulas «largas» o voladizos: elementos estructurales que por su longitud horizontal funcionan como una viga, es decir, a flexión.

Ménsulas

Las ménsulas cortas solían estar ornamentadas. En el siglo XIII el motivo ornamental era el follaje, pasando a las figuras alegóricas en los siglos XIV y XV.

Variedades de ménsula

  • Ménsula de volutas. La que forma volutas que sobresalen en los laterales.
  • Ménsula enrasada. La que no sobresalen las volutas del haz plano de los laterales.
  • Ménsula inclinada. Sigue la inclinación de una moldura.
  • Ménsula plana. La que es rectangular en su forma.
  • Mocheta. La que situándose en el ángulo superior de un vano, permite sostener un dintel o un tímpano.

Voladizos

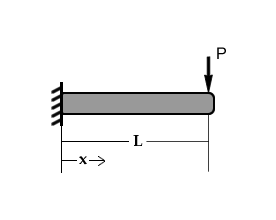
Archivo:Beam Cantilevered Load end
Ménsula o viga en voladizo.

En ingeniería, el término ménsula refiere a un tipo de viga denominado más comúnmente voladizo (en inglés cantilever) que se caracteriza por estar apoyada en solo uno de sus extremos mediante un empotramiento. Debido a la necesidad de dicho empotramiento, los voladizos suelen ser prolongaciones de vigas continuas de varios apoyos, y su longitud ideal oscila entre 1/4 y 1/5 de la longitud de los vanos intermedios, pues de esta manera se consigue equilibrar el peso en los pilares externos. Las vigas en voladizo también se usan con frecuencia en la construcción de puentes, especialmente hasta la aparición de la técnica del puente colgante.

La tensión máxima 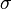\sigma\, sobre un voladizo puede ser acotada por:

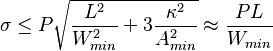
\sigma \le P \sqrt{\frac{L^2}{W_{min}^2}+ 3 \frac{\kappa^2}{A_{min}^2}} \approx \frac{PL}{W_{min}}

Donde:

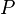P\, es la carga máxima sobre el voladizo.
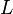L\, es la longitud del voladizo.
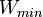W_{min}\, es el momento resistente de la sección menos resistente.
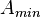A_{min}\, es el área transversal de la sección menos resistente.
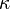\kappa\, es un factor de concentración para tensiones cortantes, a efectos prácticos puede tomarse cercano 1,5 (para un círculo 1,33).

Si además el voladizo 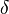\delta\, tiene una sección transversal constante y se comporta elásticamente entonces el desplazamiento vertical máximo se puede acotar por:

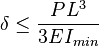
\delta \le \frac{PL^3}{3EI_{min}}

Donde:

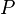P\, es la carga máxima sobre el voladizo.
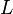L\, es la longitud del voladizo.
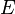E\, es el módulo de Young del material del voladizo.
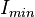I_{min}\, es el segundo momento de área de la sección menos resistente.

Véase también

Kids robot.svg En inglés: Corbel Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Ménsula&oldid=3781578»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Ménsula para Niños. Enciclopedia Kiddle.