Flexión mecánica para niños
En ingeniería, la flexión es un tipo de deformación que ocurre cuando un objeto largo se dobla. Imagina una regla que sujetas por los extremos y empujas hacia abajo en el centro: se dobla. Esa acción de doblarse es la flexión.
Este término se usa para objetos que son mucho más largos en una dirección que en las otras. Un ejemplo claro son las vigas, que son piezas de construcción diseñadas para soportar cargas principalmente doblando. El concepto de flexión también se aplica a superficies planas como placas o láminas.
Cuando un objeto se dobla, hay una parte en su interior que no se estira ni se encoge. Esta parte se llama fibra neutra. La fuerza que causa esta flexión se conoce como momento flector.
Flexión: ¿Qué es y cómo se doblan los materiales?
¿Qué es la flexión en ingeniería?
La flexión es un concepto clave en la ingeniería. Se refiere a cómo un objeto se curva o dobla cuando una fuerza lo empuja de lado. Piensa en un trampolín cuando alguien salta sobre él. Se dobla hacia abajo, y luego vuelve a su forma original. Esa es la flexión.
Este fenómeno es muy importante para diseñar estructuras. Los ingenieros deben calcular cuánto se doblará un material. Así se aseguran de que las construcciones sean seguras y estables.
¿Cómo se doblan las vigas y los arcos?
Las vigas y los arcos son partes de una estructura. Están hechas para soportar peso y doblarse un poco sin romperse. Su capacidad para resistir la flexión depende de su forma y del material.
Existen dos formas principales de entender cómo se doblan las vigas:
- La teoría de Euler-Bernoulli: Esta es una forma sencilla de calcular la flexión. Se usa para vigas largas y delgadas. Imagina que las secciones de la viga se mantienen rectas mientras se dobla.
- La teoría de Timoshenko: Esta es una forma más avanzada. Se usa para vigas más cortas y gruesas. Aquí, las secciones de la viga pueden inclinarse un poco al doblarse.
La teoría de Euler-Bernoulli: ¿Cómo funciona?
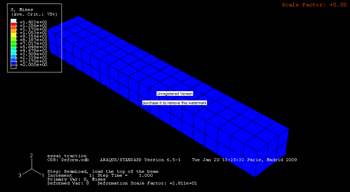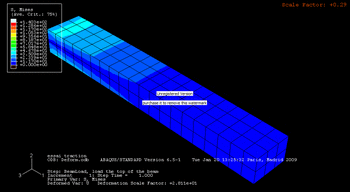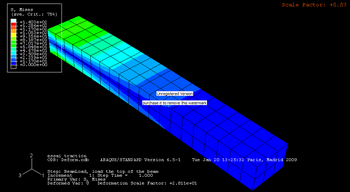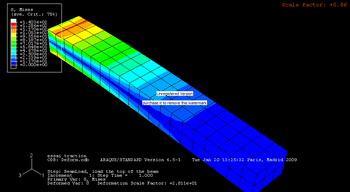
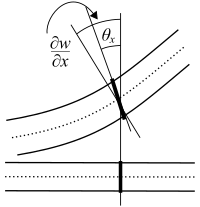
La teoría de Euler-Bernoulli es un modelo para calcular cómo se doblan las vigas. Es útil para vigas que son mucho más largas que su altura. Esta teoría ayuda a saber cuánta fuerza interna hay en la viga. También predice cuánto se moverá o "flechará" la viga.
Imagina una regla muy larga. Cuando la doblas, esta teoría te ayuda a entender cómo se distribuyen las fuerzas dentro de ella. También te dice cuánto se curvará.
La teoría de Timoshenko: ¿Cuándo se usa?
La teoría de Timoshenko es más precisa que la de Euler-Bernoulli. La diferencia principal es que la teoría de Timoshenko considera un tipo de deformación adicional. Esta deformación se debe a las fuerzas que tienden a "cortar" la viga.
Es especialmente útil para vigas que no son tan largas. Por ejemplo, si una viga es corta y gruesa, las fuerzas de corte son más importantes. La teoría de Timoshenko da un resultado más exacto en estos casos.
¿Qué pasa con las placas y láminas?
Una placa es como una viga, pero se puede doblar en dos direcciones. Piensa en una tabla de surf o una hoja de papel. Estas también experimentan flexión.
Para entender cómo se doblan las placas, hay dos teorías principales:
- La teoría de Love-Kirchhoff.
- La hipótesis de Reissner-Mindlin.
La primera es similar a la teoría de Euler-Bernoulli para vigas. La segunda es parecida a la teoría de Timoshenko.
La teoría de Love-Kirchhoff para placas
La teoría de placas de Love-Kirchhoff es un modelo para placas delgadas. Es como la teoría de Euler-Bernoulli para vigas. Se usa cuando el grosor de la placa es muy pequeño.
Esta teoría ayuda a calcular las fuerzas internas en la placa. También predice cuánto se doblará la placa. Es muy útil para diseñar objetos planos que deben soportar cargas.
La teoría de Reissner-Mindlin para placas
La teoría de Reissner-Mindlin es más avanzada para placas. Es el equivalente a la teoría de Timoshenko para vigas. A diferencia de la teoría de Love-Kirchhoff, esta considera más tipos de deformaciones.
Es más precisa para placas que no son tan delgadas. Por ejemplo, si una placa es más gruesa, esta teoría da resultados más exactos.
Véase también
 En inglés: Bending Facts for Kids
En inglés: Bending Facts for Kids
- Momento flector
- Fibra neutra
- Pendientes y deformaciones en vigas
- Núcleo central