Operador laplaciano para niños
El operador laplaciano es una herramienta matemática especial que se usa en el cálculo vectorial. Se representa con el símbolo delta (Δ) o con un nabla al cuadrado (∇²). Este operador ayuda a entender cómo cambian ciertas cantidades en el espacio.
El nombre de este operador se debe a Pierre-Simon Laplace, un famoso matemático y astrónomo francés. Él estudió ecuaciones matemáticas donde este operador aparecía con frecuencia.
En un sistema de coordenadas como el que usas para dibujar gráficas (coordenadas cartesianas), el laplaciano se calcula sumando las segundas derivadas parciales de una función. Esto significa que mide cómo una función se "curva" o "se extiende" en diferentes direcciones.
Si tenemos una cantidad que cambia en el espacio (llamada campo escalar, como la temperatura en una habitación), su laplaciano se puede escribir así:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Delta\phi= (\nabla\cdot\nabla)\phi = \nabla^2 \phi \qquad \qquad
También existe el laplaciano vectorial, que se aplica a cantidades que tienen dirección y magnitud (llamadas campos vectoriales, como la velocidad del viento).
Contenido
¿Para qué se usa el operador laplaciano?
El operador laplaciano es muy útil en diferentes áreas de la ciencia y las matemáticas.
En la física
En la física, el laplaciano aparece en muchos lugares:
- Teoría del potencial: Ayuda a describir cómo se distribuyen cosas como la gravedad o los campos eléctricos.
- Propagación de ondas: Se usa para entender cómo se mueven las ondas, como el sonido o la luz.
- Conducción del calor: Explica cómo el calor se distribuye en un objeto hasta que todo alcanza la misma temperatura.
- Electricidad: Es fundamental en la electrostática, que estudia las cargas eléctricas en reposo. Aparece en ecuaciones importantes como la ecuación de Laplace y la ecuación de Poisson.
- Mecánica cuántica: En el mundo de las partículas muy pequeñas, el laplaciano de la función de onda de una partícula nos da información sobre su energía cinética (la energía que tiene debido a su movimiento).
En las matemáticas
En las matemáticas, las funciones cuyo laplaciano es cero en una región se llaman funciones armónicas. Estas funciones son muy importantes en el estudio de las funciones complejas.
¿Por qué es tan común?
Una de las razones por las que el laplaciano aparece en tantos lugares es que las soluciones de la ecuación donde el laplaciano es cero (∇²f = 0) describen situaciones donde la energía es mínima o donde las cosas están en equilibrio. Por ejemplo, el calor se distribuye hasta que no hay más cambios, alcanzando un estado de equilibrio.
Propiedades del operador laplaciano
El laplaciano tiene algunas propiedades interesantes:
- Es lineal: Esto significa que si tienes varias funciones, puedes aplicar el laplaciano a cada una por separado y luego sumar los resultados.
:
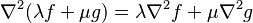
- También tiene una regla para cuando se aplica a la multiplicación de dos funciones:
:
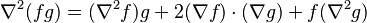
Operador laplaciano en diferentes sistemas de coordenadas
El laplaciano se puede escribir de diferentes maneras dependiendo del sistema de coordenadas que uses.
Coordenadas cartesianas
En las coordenadas cartesianas (las que usas en un plano con ejes x e y, o en el espacio con x, y, z):
- En dos dimensiones (plano):
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Delta f=\nabla^2 f= {\partial^2 f \over \partial x^2 } + {\partial^2 f \over \partial y^2 }
- En tres dimensiones (espacio):
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Delta f = \nabla^2 f = {\partial^2 f \over \partial x^2 } + {\partial^2 f \over \partial y^2 } + {\partial^2 f \over \partial z^2 }
- En cualquier número de dimensiones (n):
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Delta f(x_1,...,x_n)= \sum_{k=1}^n {\partial^2 f \over \partial x_k^2 }
Coordenadas polares
Las coordenadas polares usan una distancia (r) y un ángulo (θ) para ubicar un punto en un plano:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Delta f = \nabla^2 f = {1 \over r} {\partial \over \partial r} \left( r {\partial f \over \partial r} \right) + {1 \over r^2} {\partial^2 f \over \partial \theta^2} = {1 \over r} {\partial f \over \partial r}+{\partial^2 f\over \partial r^2}+ {1 \over r^2} {\partial^2 f \over \partial \theta^2} .
Coordenadas cilíndricas
Las coordenadas cilíndricas son útiles para objetos con forma de cilindro, usando una distancia desde el eje (ρ), un ángulo (φ) y una altura (z):
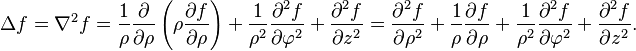
Coordenadas esféricas
Las coordenadas esféricas son buenas para objetos con forma de esfera, usando una distancia desde el centro (r) y dos ángulos (θ y φ):
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Delta f = \nabla^2 f = {1 \over r^2} {\partial \over \partial r} \left( r^2 {\partial f \over \partial r} \right) + {1 \over r^2 \sen \theta} {\partial \over \partial \theta} \left( \sen \theta {\partial f \over \partial \theta} \right) + {1 \over r^2 \sen^2 \theta} {\partial^2 f \over \partial \phi^2}
Funciones armónicas
Una función se llama armónica en una región si su laplaciano es igual a cero en todos los puntos de esa región. Por ejemplo:
- La función
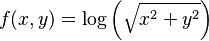es armónica en un plano. - El potencial gravitatorio de un objeto, como el de la Tierra, es armónico en el espacio que lo rodea.
- Los armónicos esféricos son funciones armónicas que se usan para resolver problemas con simetría de esfera.
Generalizaciones del Laplaciano
El laplaciano se puede extender a conceptos más complejos en matemáticas, como el operador de Laplace-Beltrami y el operador de Laplace-deRham, que se usan en áreas avanzadas de la geometría y el análisis. También hay formas de definir el laplaciano para funciones que no son "suaves" o diferenciables en todos sus puntos.
Véase también
En inglés: Laplace operator Facts for Kids
- Laplaciano vectorial
- Nabla
