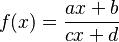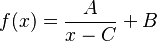Función racional para niños

En matemáticas, una función racional es un tipo especial de función. Imagina que tienes una fracción, pero en lugar de números simples, tanto la parte de arriba (el numerador) como la parte de abajo (el denominador) son polinomios.

Se puede escribir así:

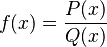
Aquí, P(x) y Q(x) son polinomios. La parte de abajo, Q(x), nunca puede ser cero. Si lo fuera, ¡no podríamos hacer la división! La palabra "racional" viene de "razón", que significa una fracción o un cociente.

Las funciones racionales son muy útiles. Se usan para aproximar o calcular los resultados de otras funciones más complicadas. Son fáciles de manejar en las computadoras, como los polinomios, pero pueden describir una variedad más grande de situaciones.

Funciones Racionales: ¿Qué Son?

¿Cómo se ven las Funciones Racionales?

Una función racional es como una fracción. En la parte de arriba y en la parte de abajo, tiene expresiones llamadas polinomios. Un polinomio es una suma de términos, donde cada término es un número multiplicado por una variable elevada a una potencia (com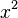o o ).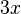

Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = \frac{x^2 + 1}{x - 3} es una función racional. Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(x) = x^2 + 1 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Q(x) = x - 3 .

¿Para qué sirven las Funciones Racionales?

Estas funciones se usan mucho en análisis numérico. Ayudan a los matemáticos y científicos a:

• Interpolar: Estimar valores entre puntos conocidos.
• Aproximar: Crear modelos más sencillos para funciones muy complejas.
• Calcular: Son fáciles de procesar en computadoras, lo que las hace muy prácticas.

Funciones Homográficas: Un Tipo Especial

¿Qué es una Función Homográfica?

Una función homográfica es un tipo particular de función racional. En este caso, el polinomio de arriba (numerador) tiene un grado igual o menor a 1. El polinomio de abajo (denominador) tiene un grado de 1.

Se ve así:

Donde a, b, c y d son números. El número c no puede ser cero. Si el denominador no es cero y se cumple una condición especial (ad ≠ bc), su gráfica es una hipérbola.

¿Dónde cruza el eje X? (Ceros)

Una función homográfica es igual a cero solo si su numerador es cero. Si tenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \textstyle f(x) = \frac{a x + b}{c x + d} , la función será cero cuando 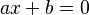. Esto ocurre cuando Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -b/a . Este valor de x es la raíz de la función. Si a es cero, la función no tiene raíces.

¿Dónde están las Asíntotas Verticales?

Las asíntotas verticales son líneas imaginarias a las que la gráfica de la función se acerca mucho, pero nunca las toca. Para una función como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \textstyle f(x) = \frac{a x + b}{c x + d} , la asíntota vertical se encuentra donde el denominador se hace cero. Como el denominador es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): cx + d , la asíntota vertical está en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -d/c .

¿Dónde están las Asíntotas Horizontales?

Las asíntotas horizontales son otras líneas imaginarias a las que la gráfica se acerca cuando x se hace muy grande o muy pequeño. Para Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \textstyle f(x) = \frac{a x + b}{c x + d} :

• Si a no es cero, la asíntota horizontal es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = a/c . Es la división de los números que acompañan a la x en el numerador y el denominador.
• Si a es cero, la asíntota horizontal es (el eje X). Esto sucede porque el grado del polinomio de abajo es mayor que el de arriba.

Otra forma de escribir las Funciones Homográficas

Las funciones homográficas también se pueden escribir de esta manera:

Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A, B, C son números reales y no es cero. Esta forma nos ayuda a ver más fácilmente cómo se dibuja la gráfica.

En esta forma:

• La asíntota vertical está en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = C . Esto es porque si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = C , el denominador Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x - C sería cero.
• La asíntota horizontal está en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = B . El valor de desplaza la asíntota horizontal hacia arriba o hacia abajo.

¿Qué pasa si B es cero?

Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): B = 0 , la asíntota horizontal es (el eje X). Esto significa que la función se acerca al eje X pero nunca lo toca. Por lo tanto, la función no tiene raíces, ya que 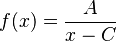nunca será cero si no es cero.

La función es positiva cuando y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x - C) tienen el mismo signo.

• Si es positivo, es positiva cuando Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x > C .
• Si es negativo, es positiva cuando Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x < C .

¿Qué pasa si C es cero y B no?

Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): C = 0 , la función es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \textstyle f(x) = \frac{A}{x }+B . En este caso, la asíntota vertical es 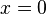(el eje Y). La asíntota horizontal sigue siendo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = B , que puede estar por encima o por debajo del eje X.

Propiedades Importantes

• Las funciones racionales son "suaves" y continuas en todos los puntos donde el denominador no es cero.
• Muchas funciones racionales tienen asíntotas (líneas a las que se acercan). Esto ocurre cuando el grado del polinomio de abajo es mayor o igual que el grado del polinomio de arriba.

Véase también

En inglés: Rational function Facts for Kids