Elipsoide de referencia para niños
Un elipsoide terrestre o esferoide terrestre es una forma matemática que se parece mucho a la forma de la Tierra. Se usa como un modelo para hacer cálculos importantes en geodesia (la ciencia que mide la Tierra), astronomía y otras ciencias de la Tierra. A lo largo de la historia, se han usado diferentes elipsoides para representar la Tierra.
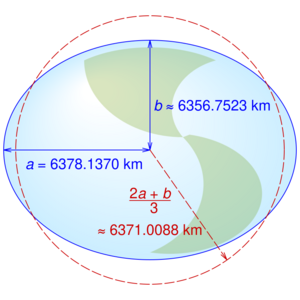
Este elipsoide es un tipo de esferoide, que es como una esfera ligeramente aplastada. Su eje más corto (el que va del polo norte al polo sur) está casi alineado con el eje sobre el que gira la Tierra. El elipsoide se define por dos medidas principales: el eje ecuatorial (que es el radio en el ecuador) y el eje polar (el radio que va del centro a los polos). La diferencia entre estos dos radios es de unos 21 kilómetros. Esto significa que la Tierra es un poco más ancha en el ecuador que de polo a polo.
Existen muchas maneras de calcular las medidas de un elipsoide terrestre. Antiguamente, se medían grandes distancias en la superficie de la Tierra. Hoy en día, se usan métodos más modernos como la geodesia satelital, que utiliza satélites para obtener medidas muy precisas. Algunos elipsoides importantes que se han usado son el de Bessel (de 1841), el de Hayford (de 1924) y el del Sistema Geodésico Mundial (WGS-84), que es el que usan los sistemas de GPS.
Contenido
La Forma de la Tierra: ¿Por qué no es una Esfera Perfecta?
¿Cómo se descubrió la forma real de la Tierra?
Desde la Antigua Grecia, la gente pensaba que la Tierra era una esfera perfecta. Sin embargo, en el siglo XVII, surgieron dudas. En 1688, el famoso científico Isaac Newton demostró con cálculos matemáticos que la rotación de la Tierra haría que se aplastara un poco en los polos y se abultara en el ecuador.
Esta idea se confirmó medio siglo después, gracias a dos expediciones de la Academia Francesa de Ciencias. Una fue al norte, cerca del polo, y la otra fue a lo que hoy es Ecuador, cerca de la línea ecuatorial. Sus mediciones demostraron que la Tierra estaba achatada, confirmando lo que Newton había predicho. Esta forma se convirtió en el nuevo modelo de referencia para la Tierra.
El metro y la forma de la Tierra
La medición de la Tierra también ayudó a definir el metro. En 1791, el metro se definió como una diezmillonésima parte de la distancia ideal desde el polo hasta el ecuador. Hubo algunos errores en las primeras mediciones, por lo que la definición del metro se ajustó varias veces. Finalmente, en 1983, el metro se redefinió de una manera más precisa, basándose en la distancia que recorre la luz en el vacío en un tiempo determinado.
El experimento del péndulo de Jean Richer
En 1671, un astrónomo francés llamado Jean Richer viajó a Cayena, en la Guayana Francesa, cerca del ecuador. Llevaba un reloj de péndulo que funcionaba perfectamente en París. Pero en Cayena, el reloj empezó a atrasarse casi dos minutos y medio al día.
Cuando se publicaron las leyes de la gravedad de Newton en 1687, se entendió por qué. La gravedad es un poco menor cerca del ecuador porque esa zona está un poco más lejos del centro de la Tierra. Esto se debe a que la Tierra está abultada en el ecuador y aplastada en los polos. Esta forma se conoce como elipsoide achatado.
Tipos de Elipsoides Terrestres
Existen dos tipos principales de elipsoides: el medio y el de referencia.
- Un elipsoide terrestre medio es un modelo que describe la curvatura promedio de toda la superficie de la Tierra. Es como una representación ideal de la forma global de nuestro planeta. Se busca que tenga el mismo volumen que el geoide, que es la forma que tendría la superficie de los océanos si no hubiera mareas ni corrientes, extendida bajo los continentes.
- Los elipsoides de referencia se usan para regiones más pequeñas o países específicos. Aunque el elipsoide medio es ideal para mediciones globales, para mapas y mediciones locales es mejor usar un elipsoide que se ajuste mejor a la curvatura de esa región en particular. Esto ayuda a que los cálculos sean más precisos y a evitar pequeñas distorsiones.
Por eso, algunos elipsoides antiguos, como el de Hayford o el de Bessel, siguen siendo importantes para ciertos mapas y límites territoriales. Si se cambiara el elipsoide de referencia, las coordenadas de millones de puntos de referencia también cambiarían, lo que podría causar problemas legales. Sin embargo, para sistemas globales como el GPS o la astronáutica, se usan los elipsoides más modernos y precisos, que se actualizan a medida que se obtiene más información sobre la forma de la Tierra.
¿Cómo se describe un Elipsoide?
En geofísica y geodesia, cuando se habla de "elipsoide", casi siempre se refieren a un elipsoide achatado por los polos. La forma de este elipsoide se define por dos medidas principales de la elipse que lo forma:
- El semieje mayor (llamado a) es el radio de la Tierra en el ecuador.
- El semieje menor (llamado b) es la distancia desde el centro de la Tierra hasta cualquiera de los polos.
Estas dos medidas son suficientes para describir completamente la forma del elipsoide.
Además de a y b, se usa otro valor importante llamado achatamiento (representado por f). El achatamiento nos dice cuánto está aplastada la Tierra en los polos en comparación con su radio en el ecuador. Se calcula con la fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f=\frac{a-b}{a}. A menudo, el achatamiento se expresa como una fracción, por ejemplo, 1/298. Esto significa que por cada 298 unidades de radio ecuatorial, la diferencia entre el radio ecuatorial y el polar es de 1 unidad.
El elipsoide WGS-84, que es el que se usa en la mayoría de los sistemas de GPS y mapas, tiene un achatamiento de aproximadamente 1/298. Esto significa que la diferencia entre su radio ecuatorial y polar es de unos 21 kilómetros. Para que te hagas una idea, la Luna es aún menos achatada que la Tierra, mientras que el planeta Júpiter está mucho más achatado, ¡casi 1/15!
¿Cómo se determina un Elipsoide?
Históricamente, la forma del elipsoide se determinaba midiendo grandes arcos de meridiano en la superficie de la Tierra. Con al menos dos de estas mediciones, se podían calcular los parámetros del elipsoide.
Hoy en día, la geodesia moderna utiliza métodos mucho más avanzados, como la geodesia satelital. Los satélites que orbitan la Tierra pueden medir con gran precisión la distancia a diferentes puntos de la superficie y también la gravedad en distintos lugares. Estas mediciones permiten determinar la forma de la Tierra de manera muy exacta.
Elipsoides terrestres históricos
A lo largo de la historia, se han usado muchos modelos de elipsoides para representar la Tierra. Algunos de los más antiguos llevan el nombre de la persona que los definió y el año en que lo hicieron. Por ejemplo, el coronel Alexander Ross Clarke recibió una medalla en 1887 por su trabajo en la determinación de la forma de la Tierra. El elipsoide internacional, desarrollado por John Fillmore Hayford en 1910, fue adoptado por la Unión Internacional de Geodesia y Geofísica (IUGG) en 1924 para uso mundial.
Más tarde, en 1967, la IUGG recomendó el elipsoide GRS-67 (Sistema de Referencia Geodésico 1967) para una mayor precisión. Este se usó en lugares como Australia y América del Sur. El GRS-80 (Sistema de Referencia Geodésica de 1980), aprobado en 1979, es aún más preciso y se basa en el radio ecuatorial, la masa total de la Tierra, un factor de forma dinámico y la velocidad de rotación. El elipsoide WGS-84, muy usado hoy en día, es muy similar al GRS-80.
Es importante saber que un modelo de elipsoide describe solo la forma geométrica. A menudo, forma parte de un sistema de referencia geodésico más grande, que incluye también información sobre la gravedad. Por ejemplo, el sistema WGS84 es tanto un modelo de elipsoide como un sistema de referencia completo.
A continuación, se muestra una tabla con algunos de los elipsoides históricos más importantes:
| Nombre del elipsoide de referencia | Radio ecuatorial (m) | Radio polar (m) | Aplanamiento inverso | Dónde se utiliza |
|---|---|---|---|---|
| Maupertuis (1738) | 6.397.300 | 6.363.806,283 | 191 | Francia |
| Plessis (1817) | 6.376.523,0 | 6.355.862,9333 | 308,64 | Francia |
| Everest (1830) | 6.377.299,365 | 6.356.098,359 | 300,80172554 | India |
| Everest 1830 Modified (1967) | 6.377.304,063 | 6.356.103,0390 | 300,8017 | Malasia Occidental & Singapur |
| Everest 1830 (1967 Definition) | 6.377.298,556 | 6.356.097,550 | 300,8017 | Brunéi & Malasia Oriental |
| Airy (1830) | 6.377.563,396 | 6.356.256,909 | 299,3249646 | Gran Bretaña |
| Bessel (1841) | 6.377.397,155 | 6.356.078,963 | 299,1528128 | Europa. Japón |
| Clarke (1866) | 6.378.206,4 | 6.356.583,8 | 294,9786982 | América del Norte |
| Clarke (1878) | 6.378.190 | 6.356.456 | 293,4659980 | América del Norte |
| Clarke (1880) | 6.378.249,145 | 6.356.514,870 | 293,465 | Francia. África |
| Helmert (1906) | 6.378.200 | 6.356.818,17 | 298,3 | Egipto |
| Hayford (1910) | 6.378.388 | 6.356.911,946 | 297 | Estados Unidos |
| International (1924) | 6.378.388 | 6.356.911,946 | 297 | Europa |
| Krassovsky (1940) | 6.378.245 | 6.356.863,019 | 298,3 | URSS. Rusia. Rumanía |
| WGS66 (1966) | 6.378.145 | 6.356.759,769 | 298,25 | Estados Unidos/Departamento de Defensa |
| Australian National (1966) | 6.378.160 | 6.356.774,719 | 298,25 | Australia |
| New International (1967) | 6.378.157,5 | 6.356.772,2 | 298,24961539 | |
| GRS-67 (1967) | 6.378.160 | 6.356.774,516 | 298,247167427 | |
| South American (1969) | 6.378.160 | 6.356.774,719 | 298,25 | América del Sur |
| WGS-72 (1972) | 6.378.135 | 6.356.750,52 | 298,26 | Estados Unidos/Departamento de Defensa |
| GRS-80 (1979) | 6.378.137 | 6.356.752,3141 | 298,257222101 | Global ITRS |
| WGS-84 (1984) | 6.378.137 | 6.356.752,3142 | 298,257223563 | Global GPS |
| Servicio Internacional de Rotación de la Tierra y Sistemas de Referencia (1989) | 6.378.136 | 6.356.751,302 | 298,257 | |
| IERS (2003) | 6,378,136.6 | 6,356,751.9 | 298.25642 |
Véase también
 En inglés: Reference ellipsoid Facts for Kids
En inglés: Reference ellipsoid Facts for Kids
- Protuberancia ecuatorial
- Radio terrestre
- Sistema de referencia geodésico
- Arco de meridiano
- Gravedad normal
- Historia de la geodesia