Ápside para niños
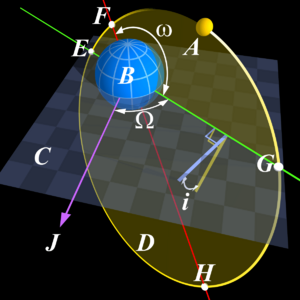
En astronomía, un ápside es un punto especial en la órbita de un objeto alrededor de otro. Imagina que un planeta gira alrededor de una estrella en un camino con forma de óvalo (una elipse). El ápside se refiere a los dos puntos donde el planeta está más cerca o más lejos de la estrella.
El punto donde el objeto está más cerca de su centro de atracción se llama periápside. El punto donde está más lejos se llama apoápside. La línea recta que une el periápside y el apoápside se conoce como la línea de ápsides. Esta línea es como el eje más largo de la forma ovalada de la órbita.
Contenido
¿Cómo se llaman los ápsides para diferentes cuerpos celestes?
Cuando un objeto orbita un cuerpo específico, usamos nombres especiales para el periápside y el apoápside.
- Para el Sol, los puntos se llaman perihelio (el más cercano) y afelio (el más lejano).
- Para la Tierra, se usan los términos perigeo (el más cercano) y apogeo (el más lejano).
- Para la Luna, se usan periselenio y aposelenio.
Estos nombres nos ayudan a saber rápidamente de qué cuerpo celeste estamos hablando.
¿Por qué las órbitas son elípticas?
Según las leyes del movimiento de Newton, la mayoría de las órbitas en el espacio son elipses, no círculos perfectos. Esto se debe a la forma en que la gravedad actúa entre dos objetos. El centro de gravedad de dos cuerpos (llamado baricentro) puede estar dentro del cuerpo más grande. Por ejemplo, el baricentro de la Tierra y la Luna está dentro de la Tierra.
Cuando hablamos de la distancia de un ápside, nos referimos a la distancia entre el centro de un objeto y el centro del objeto que orbita. Sin embargo, para las naves espaciales, a menudo se usa la altura de la nave sobre la superficie del planeta.
Terminología de los ápsides
Existen muchos términos para los ápsides, dependiendo del cuerpo que se orbita. Aquí tienes algunos ejemplos:
| Cuerpo | Punto más cercano | Punto más lejano |
|---|---|---|
| Galaxia | Perigaláctico | Apogaláctico |
| Estrella | Periastro | Apoastro |
| Agujero negro | Perimelasma/Perinigricon | Apomelasma/Aponigricon |
| Sol | Perihelio | Afelio |
| Tierra | Perigeo | Apogeo |
| Luna | Periselenio/Pericintio/Perilunio | Aposelenio/Apocintio/Apolunio |
| Mercurio | Perihermo | Afhermo |
| Venus | Pericitera/Pericritio | Apocitera/Apocritio |
| Marte | Periareion | Apoareion |
| Júpiter | Perijovio/Perizeno | Apojovio/Apozeno |
| Saturno | Pericrono/Perisaturnio | Apokrono/Aposaturnio |
| Urano | Periuranio | Apouranio |
| Neptuno | Periposeidinion | Apoposeidinion |
| Plutón | Perihadio | Apohadio |
Aunque hay muchos nombres específicos, el término -ápside se usa a menudo de forma general para evitar confusiones.
Perihelio y afelio de la Tierra
La Tierra no orbita el Sol en un círculo perfecto. Por eso, hay momentos en que está más cerca y más lejos del Sol.
- La Tierra alcanza su perihelio (punto más cercano al Sol) a principios de enero. En este momento, estamos a unos 147 millones de kilómetros del Sol.
- La Tierra alcanza su afelio (punto más lejano al Sol) a principios de julio. Aquí, la distancia es de unos 152 millones de kilómetros.
Estas fechas cambian un poco con el tiempo debido a movimientos lentos de la órbita terrestre, conocidos como ciclos de Milankovitch.
¿Afectan los ápsides a las estaciones?
Aunque la Tierra está más cerca del Sol en enero y más lejos en julio, esto no es lo que causa las estaciones. Las estaciones se deben principalmente a la inclinación del eje de la Tierra. Cuando un hemisferio está inclinado hacia el Sol, recibe más luz directa y es verano. Cuando está inclinado lejos del Sol, recibe menos luz directa y es invierno.
Sin embargo, los ápsides sí tienen un efecto indirecto. La Tierra se mueve más rápido cuando está en el perihelio y más lento cuando está en el afelio. Esto significa que el verano en el hemisferio norte dura un poco más (93 días) que el verano en el hemisferio sur (89 días).
Tiempo de perihelio para cometas y planetas
Los astrónomos calculan cuándo un objeto, como un cometa o un planeta, pasará por su perihelio. Estos cálculos son muy importantes para predecir su trayectoria. Para objetos que están muy lejos del Sol, como algunos objetos transneptunianos, se necesitan muchas observaciones durante varios años para calcular su órbita con precisión.
Por ejemplo, se calcula que el planeta enano Eris llegará a su perihelio alrededor de diciembre de 2257.
Véase también
 En inglés: Apsis Facts for Kids
En inglés: Apsis Facts for Kids
- Afelio
- Perihelio
- Apogeo
- Perigeo
- Órbita elíptica
- Mecánica celeste

