Semieje mayor y semieje menor para niños
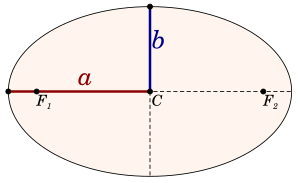
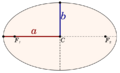
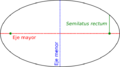
En geometría, el eje mayor de una elipse es su línea más larga. Es un segmento que atraviesa el centro de la elipse y pasa por sus dos focos. Sus extremos son los dos puntos más alejados del borde de la elipse.
El semieje mayor es la mitad del eje mayor. Se extiende desde el centro de la elipse, pasa por uno de los focos y llega hasta el borde. Es como el "radio más largo" de una elipse.
El semieje menor de una elipse o hipérbola es un segmento de línea que forma un ángulo recto con el semieje mayor. Uno de sus extremos está en el centro de la curva. En el caso especial de un círculo, las longitudes de los semiejes mayor y menor son iguales a su radio.
Los ejes mayor y menor son como los "espejos" de la curva, es decir, sus ejes de simetría. En una elipse, el eje menor es el más corto. En una hipérbola, es el eje que no cruza la curva.
Contenido
Elipse: Formas y Medidas
Una elipse se puede describir con una ecuación matemática que nos ayuda a entender su forma. Si el centro de la elipse está en un punto (h, k) en un plano cartesiano, la ecuación es:
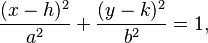
Aquí, a es la longitud del semieje mayor y b es la longitud del semieje menor.
El semieje mayor (a) también se puede calcular como el promedio de las distancias máxima y mínima desde uno de los focos hasta el borde de la elipse. Estas distancias se miden en los puntos más alejados y más cercanos al foco. En astronomía, estos puntos se llaman ápsides.
El semieje menor (b) de una elipse se puede encontrar usando una fórmula que relaciona las distancias máxima y mínima desde un foco.
La excentricidad (e) de una elipse nos dice qué tan "aplanada" es. Si la excentricidad es cero, la elipse es un círculo perfecto. Cuanto mayor sea la excentricidad (cercana a 1), más alargada será la elipse.
Una parábola es como una elipse muy, muy alargada. Imagina una secuencia de elipses donde uno de los focos se queda quieto y el otro se aleja mucho. Al final, esa elipse se convierte en una parábola.
Hipérbola: Otra Curva Cónica
El semieje mayor de una hipérbola se define como la mitad de la distancia más corta entre sus dos ramas. Si el semieje mayor es a en la dirección x, la ecuación de una hipérbola es:
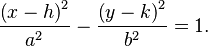
En una hipérbola, el eje mayor se llama eje transversal. También existe un eje conjugado o eje menor, que es perpendicular al eje transversal. Este eje menor tiene una longitud de 2b. El semieje menor (b) es la mitad de esta longitud.
El semieje menor de una hipérbola también es la distancia desde uno de sus focos hasta una de sus asíntotas (líneas a las que la curva se acerca infinitamente sin tocarlas).
El Eje Mayor en la Astronomía
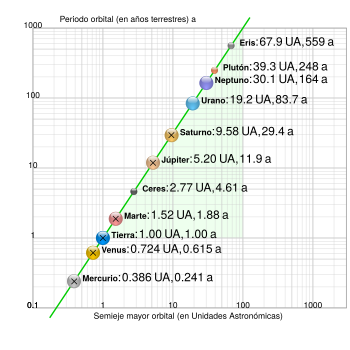
En astrodinámica, que es el estudio del movimiento de los objetos en el espacio, el semieje mayor es muy importante. Nos ayuda a calcular el período orbital (el tiempo que tarda un objeto en dar una vuelta completa) de un cuerpo que orbita alrededor de otro.
El período orbital (T) de un objeto pequeño que gira alrededor de un cuerpo central en una órbita circular o elíptica se calcula con la siguiente fórmula:
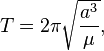
Donde:
- a es la longitud del semieje mayor de la órbita.
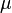es una constante relacionada con la gravedad del cuerpo central.
Es interesante saber que, para todas las elipses con el mismo semieje mayor, el período orbital es el mismo, sin importar qué tan "aplanada" sea la órbita (su excentricidad).
El semieje mayor es uno de los elementos orbitales más importantes de una órbita. Para los objetos de nuestro sistema solar, el semieje mayor está relacionado con el período de la órbita por la tercera ley de Kepler. Esta ley dice que el cuadrado del período orbital (T²) es proporcional al cubo del semieje mayor (a³):
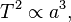
Esta fórmula fue descubierta por Johannes Kepler y luego explicada por Isaac Newton con su ley de la gravitación universal. La fórmula completa de Newton es:
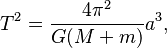
Aquí, G es la constante de gravitación universal, M es la masa del cuerpo central (como el Sol) y m es la masa del cuerpo que orbita (como un planeta). Generalmente, la masa del cuerpo central es mucho mayor, por lo que la masa del objeto en órbita (m) se puede ignorar para simplificar el cálculo.
¿Qué tan elípticas son las órbitas planetarias?
Las órbitas de los planetas son ejemplos famosos de elipses, gracias a la primera ley de Kepler. Sin embargo, la diferencia entre el semieje mayor y el semieje menor de las órbitas planetarias es muy pequeña. Esto significa que, en realidad, las órbitas de los planetas son casi circulares.
La idea de que las órbitas son muy elípticas viene de la gran diferencia entre el afelio (el punto más lejano al Sol) y el perihelio (el punto más cercano al Sol). Esta diferencia es mucho más notoria que la diferencia entre los semiejes.
| Excentricidad | Semieje mayor a (UA) | Semieje menor b (UA) | Diferencia (%) | Perihelio (UA) | Afelio (UA) | Diferencia (%) | |
|---|---|---|---|---|---|---|---|
| Mercurio | 0.206 | 0.38700 | 0.37870 | 2.2 | 0.307 | 0.467 | 52 |
| Venus | 0.007 | 0.72300 | 0.72298 | 0.002 | 0.718 | 0.728 | 1.4 |
| Tierra | 0.017 | 1.00000 | 0.99986 | 0.014 | 0.983 | 1.017 | 3.5 |
| Marte | 0.093 | 1.52400 | 1.51740 | 0.44 | 1.382 | 1.666 | 21 |
| Júpiter | 0.049 | 5.20440 | 5.19820 | 0.12 | 4.950 | 5.459 | 10 |
| Saturno | 0.057 | 9.58260 | 9.56730 | 0.16 | 9.041 | 10.124 | 12 |
| Urano | 0.046 | 19.21840 | 19.19770 | 0.11 | 18.330 | 20.110 | 9.7 |
| Neptuno | 0.010 | 30.11000 | 30.10870 | 0.004 | 29.820 | 30.400 | 1.9 |
Galería de imágenes
-
El semieje mayor (a) y el semieje menor (b) de una elipse
-
Eje mayor (rojo), eje menor (azul) y semilatus rectum (verde) de una elipse
-
Gráfico logarítmico del período T frente al semieje mayor a de algunas órbitas del Sistema Solar. Muestra que a³/T² es constante (línea verde)
Véase también
En inglés: Semi-major axis Facts for Kids
