Ecuación para niños

Enciclopedia para niños

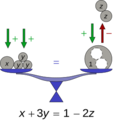
Una ecuación es como un rompecabezas matemático donde tienes una igualdad entre dos expresiones. Imagina una balanza en equilibrio: lo que pones en un lado debe ser igual a lo que pones en el otro. En una ecuación, los dos lados están separados por el signo "igual" (=).

En estas expresiones, hay cosas que conoces (como números o valores fijos) y cosas que no conoces, llamadas incógnitas. Las incógnitas suelen representarse con letras, como la x, la y o la z. El objetivo es encontrar el valor de esas incógnitas para que la igualdad sea verdadera.

Por ejemplo, en la ecuación:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3x-1=9+x

Aquí, la x es la incógnita. Los números 3, 1 y 9 son valores conocidos. Para que esta igualdad sea cierta, la x debe tener un valor específico. En este caso, la solución es:

$x = 5$

Si sustituyes x por 5 en la ecuación, verás que ambos lados dan el mismo resultado: 3 * 5 - 1 = 15 - 1 = 14 9 + 5 = 14 ¡Así que 14 = 14! La igualdad se cumple.

Si una igualdad es siempre verdadera, sin importar el valor de la incógnita, se llama identidad. Por ejemplo, 2x + x = 3x es una identidad, porque siempre es cierta para cualquier valor de x.

El símbolo "=" fue creado en 1557 por un matemático llamado Robert Recorde. Él pensó que no había nada más igual que dos líneas rectas paralelas de la misma longitud.

Las ecuaciones son muy útiles en muchas áreas, desde la ciencia hasta la vida diaria. Nos ayudan a describir relaciones entre diferentes cantidades y a resolver problemas.

El primer uso del signo de igualdad. La ecuación equivale a la notación moderna

14 x + 15 = 71

¿Qué es una Ecuación?

Una ecuación es una afirmación de que dos expresiones matemáticas son iguales. Se escribe con un signo de igualdad (=) entre ellas. El lado izquierdo del signo igual se llama "primer miembro" y el lado derecho se llama "segundo miembro". A menudo, el segundo miembro de una ecuación es cero, pero esto no cambia su significado, ya que siempre podemos restar el lado derecho de ambos lados para que sea cero.

Partes de una Ecuación

Las ecuaciones suelen tener:

Incógnitas: Son los valores que queremos encontrar, representados por letras (como x, y, z).
Constantes o Coeficientes: Son números conocidos que acompañan a las incógnitas o están solos.
Operaciones: Son las acciones matemáticas que relacionan los números y las incógnitas (suma, resta, multiplicación, división, etc.).

Por ejemplo, en la ecuación: $Ax^2 +Bx + C - y = 0$ Aquí, x e y son las incógnitas, y A, B y C son parámetros o coeficientes que se consideran conocidos en un problema específico.

Una ecuación es una igualdad. La incógnita satisface dicha igualdad con valor determinado.

La Ecuación como una Balanza

Piensa en una ecuación como una balanza de dos platillos. Si pones el mismo peso en ambos platillos, la balanza se mantiene en equilibrio. Si quitas peso de un lado, debes quitar la misma cantidad del otro para que siga en equilibrio. De la misma manera, una ecuación se mantiene en equilibrio si realizas la misma operación (sumar, restar, multiplicar, dividir) en ambos lados.

Parámetros e Incógnitas: ¿Cuál es la Diferencia?

Además de las incógnitas, las ecuaciones pueden contener otros términos que se consideran conocidos. Estos se llaman constantes, coeficientes o parámetros.

Por ejemplo, la ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 +y^2 = R^2 Aquí, x e y son las incógnitas. R es un parámetro. Si le damos a R el valor de 2 (R = 2), esta ecuación describe un círculo con radio 2 en un plano. Si R no está especificado, la ecuación representa cualquier círculo centrado en el origen.

Generalmente, las incógnitas se escriben con las últimas letras del alfabeto (x, y, z), y los parámetros o coeficientes con las primeras (a, b, c).

Resolver una ecuación significa encontrar los valores de las incógnitas que hacen que la igualdad sea cierta.

Sistemas de Ecuaciones

A veces, tenemos varias ecuaciones que deben cumplirse al mismo tiempo. Esto se llama un sistema de ecuaciones. La solución de un sistema es un conjunto de valores para todas las incógnitas que funcionan en cada una de las ecuaciones del sistema.

Por ejemplo, este sistema: 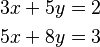$\begin{align} 3x+5y&=2\\ 5x+8y&=3 \end{align}$ Tiene una única solución: x = -1, y = 1.

¿Para qué se Usan las Ecuaciones?

Las ecuaciones son fundamentales en la ciencia y la tecnología. Nos permiten describir leyes y relaciones de forma precisa.

En física, la famosa segunda ley de Newton (F = ma) relaciona la fuerza (F), la masa (m) y la aceleración (a). Si conoces dos de estos valores, puedes usar la ecuación para encontrar el tercero.
En economía, se usan para calcular intereses, porcentajes o costos.
En geometría, las ecuaciones nos ayudan a describir formas como líneas, círculos o planos.

Las ecuaciones nos permiten entender cómo se relacionan las cosas en el mundo real y resolver problemas complejos.

Tipos de Ecuaciones

Existen muchos tipos de ecuaciones, que se clasifican según las operaciones que contienen y el tipo de números que buscamos como solución.

Ecuaciones Algebraicas

Son las ecuaciones más comunes y contienen solo expresiones algebraicas (polinomios, fracciones con polinomios, raíces, etc.).

Ecuaciones de Primer Grado (Lineales):

* La incógnita (generalmente x) está elevada a la potencia 1. * Forma: 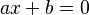$ax + b = 0$ (donde a y b son números, y a no es cero). * Ejemplo: 5x + 3 = 2x * Su solución es sencilla: 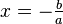$x = -\tfrac{b}{a}$ . * Cuando las dibujas en una gráfica, forman una línea recta.

Ecuaciones de Segundo Grado (Cuadráticas):

* La incógnita está elevada a la potencia 2 (al cuadrado). * Forma: 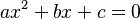$ax^2+bx+c=0$ (donde a, b y c son números, y a no es cero). * Ejemplo: x² - 5x + 3 = 0 * Estas ecuaciones pueden tener hasta dos soluciones. * Cuando las dibujas en una gráfica, forman una curva llamada parábola.

Ecuaciones de Tercer Grado (Cúbicas):

* La incógnita está elevada a la potencia 3 (al cubo). * Ejemplo: x³ + x² - 6x = 0

Ecuaciones Diofánticas:

* Son ecuaciones donde solo buscamos soluciones que sean números enteros.

Otros Tipos de Ecuaciones

Ecuaciones Trascendentes: Contienen funciones más complejas que los polinomios, como funciones trigonométricas (seno, coseno), exponenciales o logarítmicas.
Ecuaciones Diferenciales: Relacionan una función con sus derivadas (la tasa de cambio de la función). Son muy importantes en física, ingeniería y biología para modelar cómo cambian las cosas con el tiempo.
Ecuaciones Integrales: Involucran integrales de funciones desconocidas.
Ecuaciones Funcionales: Las incógnitas son funciones, no solo números.

Propiedades de las Ecuaciones

Dos ecuaciones son equivalentes si tienen las mismas soluciones. Podemos transformar una ecuación en otra equivalente realizando las mismas operaciones en ambos lados:

Sumar o restar la misma cantidad a ambos lados.
Multiplicar o dividir ambos lados por la misma cantidad (que no sea cero).
Usar una identidad para simplificar un lado de la ecuación.

¡Cuidado! Si aplicas una función a ambos lados de una ecuación, la nueva ecuación puede tener más soluciones que la original. Por ejemplo, si tienes x = 1 y elevas ambos lados al cuadrado, obtienes x² = 1. Esta nueva ecuación tiene dos soluciones (x=1 y x=-1), mientras que la original solo tenía una.

Las propiedades básicas de las ecuaciones son:

Propiedad Reflexiva: Cualquier cosa es igual a sí misma (a = a). Ejemplo: 14 = 14.
Propiedad Simétrica: Si a = b, entonces b = a. Ejemplo: Si x = 5, entonces 5 = x.
Propiedad Transitiva: Si a = b y b = c, entonces a = c. Ejemplo: Si x = y y y = 10, entonces x = 10.

Resolución de Ecuaciones

Resolver una ecuación significa encontrar el conjunto de todos los valores de las incógnitas que hacen que la igualdad sea verdadera. A veces, una ecuación no tiene solución (el conjunto de soluciones está vacío), o puede tener una, varias o incluso infinitas soluciones.

Historia de las Ecuaciones

Las ecuaciones no son algo nuevo; la gente ha estado resolviendo problemas similares a las ecuaciones desde hace miles de años.

Antigüedad

Los egipcios (hace más de 3500 años) ya resolvían problemas de reparto que eran como ecuaciones simples de primer grado. Usaban un método de "falsa posición" para encontrar soluciones aproximadas.
Los matemáticos chinos (alrededor del inicio de nuestra era) tenían métodos para resolver ecuaciones de primer y segundo grado, e incluso sistemas de ecuaciones.
El matemático griego Diofanto de Alejandría (siglo III d.C.) escribió un libro llamado Arithmetica donde trataba ecuaciones de primer y segundo grado. Fue uno de los primeros en usar símbolos para representar las ecuaciones. También estudió las ecuaciones diofánticas, que son aquellas con soluciones que deben ser números enteros.

Siglos XV y XVI

En la Edad Moderna, el estudio de las ecuaciones avanzó mucho. En el siglo XV, eran populares los desafíos matemáticos. Niccolò Fontana Tartaglia ganó un famoso desafío al resolver ecuaciones de tercer grado.
Más tarde, los matemáticos italianos Girolamo Cardano y Rafael Bombelli descubrieron que para resolver todas las ecuaciones de segundo, tercer y cuarto grado, eran necesarios los números imaginarios.
En el mismo siglo, el francés René Descartes popularizó la forma en que escribimos las ecuaciones hoy en día: usando las primeras letras del alfabeto (a, b, c) para los valores conocidos y las últimas (x, y, z) para las incógnitas.

Siglos XVII y XVIII

En el siglo XVII, Isaac Newton y Gottfried Leibniz desarrollaron los primeros métodos para resolver las ecuaciones diferenciales, que son muy importantes para entender el movimiento y los cambios en la naturaleza.

Época Moderna

A principios del siglo XIX, los matemáticos Niels Henrik Abel y Évariste Galois demostraron algo sorprendente: no existe una fórmula general para resolver ecuaciones de quinto grado o superiores usando solo operaciones básicas y raíces.
En el siglo XIX, las ecuaciones diferenciales se volvieron aún más importantes en la física, por ejemplo, en las leyes del electromagnetismo de James Clerk Maxwell.
En el siglo XX, las ecuaciones se usaron para describir fenómenos aún más complejos, como la mecánica cuántica (con ecuaciones de Erwin Schrödinger) y la Relatividad General de Albert Einstein.
Hoy en día, con la ayuda de las computadoras, podemos resolver ecuaciones con millones de incógnitas usando métodos numéricos (aproximaciones).

Las Ecuaciones en la Geometría

Geometría Analítica

Una sección cónica es la intersección de un plano y un cono de revolución.

La geometría analítica es una rama de las matemáticas que une la geometría euclidiana (el estudio de las formas y el espacio) con el álgebra (el estudio de las ecuaciones). Esto se logra asignando coordenadas a cada punto en el espacio.

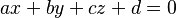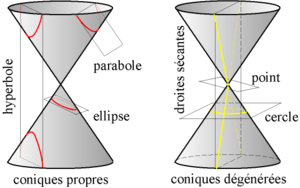
Por ejemplo, un plano en un espacio tridimensional se puede describir con una ecuación como $ax+by+cz+d=0$ . Los valores x, y, z son las coordenadas de los puntos que forman el plano.
Las secciones cónicas (círculos, elipses, parábolas, hipérbolas) se pueden describir como la intersección de un cono y un plano, y cada una tiene su propia ecuación.

Esta idea, desarrollada por René Descartes, revolucionó las matemáticas porque permitió usar las herramientas del álgebra para resolver problemas de geometría.

Ecuaciones Cartesianas

Archivo:Cartesian-coordinate-system-with-circle

Sistema de coordenadas cartesianas con un círculo de radio 2 centrado en el origen marcado en rojo. La ecuación de un círculo es (x − a)² + (y − b)² = r² donde a y b son las coordenadas del centro (a, b) y r es el radio.

Un sistema de coordenadas cartesianas nos permite ubicar cualquier punto en un plano o en el espacio usando números. Por ejemplo, en un plano, un punto se define por un par de coordenadas (x, y).

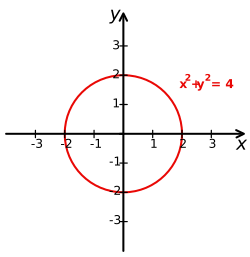
Usando este sistema, las formas geométricas se pueden describir con ecuaciones cartesianas. Por ejemplo, un círculo con radio 2 y centro en el origen se describe con la ecuación: 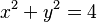$x^2 + y^2 = 4$ . Cualquier punto (x, y) que cumpla esta ecuación estará en el círculo.

Ecuaciones Paramétricas

Una ecuación paramétrica describe las coordenadas de los puntos de una curva o superficie como funciones de una o más variables, llamadas parámetros. Por ejemplo, las ecuaciones: 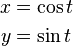$\begin{align} x&=\cos t\\ y&=\sin t \end{align}$ Son las ecuaciones paramétricas para un círculo unitario, donde t es el parámetro. A medida que t cambia, los valores de x e y cambian, dibujando el círculo.

Ejemplos Famosos de Ecuaciones

Ecuaciones de Maxwell: Describen cómo funcionan la electricidad y el magnetismo.
Ecuaciones de Navier-Stokes: Describen el movimiento de los fluidos (como el agua o el aire).
Ecuación de onda: Describe cómo se propagan las ondas (sonido, luz).
Ecuación de Schrödinger: Fundamental en la mecánica cuántica, describe el comportamiento de las partículas muy pequeñas.
Ecuación del Teorema de Pitágoras: 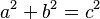$a^2 + b^2 = c^2$ , relaciona los lados de un triángulo rectángulo.

Galería de imágenes

Ilustración de una ecuación simple; x , y , z son números reales, análogos a los pesos.
Las soluciones -1 y 2 de la ecuación polinómica x² - x + 2 = 0 son los puntos donde la gráfica de la función cuadrática y = x² - x + 2 corta el eje de las x.
Un Atractor, que surge al resolver una determinada ecuación diferencial

Véase también

En inglés: Equation Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Ecuación&oldid=4736718»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Ecuación para Niños. Enciclopedia Kiddle.