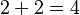Igualdad matemática para niños
Una igualdad matemática es una afirmación en la que dos expresiones representan el mismo valor o el mismo objeto en matemáticas. Cuando decimos que dos cosas son "iguales", significa que tienen exactamente el mismo valor.
Por ejemplo, la frase "la suma de dos y dos" y la palabra "cuatro" se refieren al mismo número. En matemáticas, usamos el signo = para mostrar que algo es igual. Así, el ejemplo anterior se escribe como:
Esto significa que el resultado de sumar 2 más 2 es el mismo que el número 4.
Contenido
Origen del signo de igualdad
El signo = que usamos hoy para indicar que algo es igual fue inventado por un matemático llamado Robert Recorde en el año 1557.
Recorde estaba cansado de escribir la frase "es igual a" una y otra vez en sus libros. Por eso, decidió usar un par de líneas paralelas (——) en su obra llamada Whetstone of Witte. Con la publicación de este libro, Recorde introdujo por primera vez el álgebra en Inglaterra, y con ella, este práctico símbolo.
La igualdad en los conjuntos
En matemáticas, un conjunto es una colección de elementos.
- Dos conjuntos son considerados iguales si tienen exactamente los mismos elementos. Esto se conoce como el axioma de la extensión.
- También podemos decir que un conjunto A es igual a un conjunto B si todos los elementos de A están en B, y al mismo tiempo, todos los elementos de B están en A.
Una relación de equivalencia es una forma de agrupar los elementos de un conjunto que tienen algo en común. Cuando aplicamos una relación de equivalencia, el conjunto se divide en grupos llamados clases de equivalencia. Todos los elementos dentro de una misma clase son "equivalentes" entre sí.
Por ejemplo, podemos dividir los números naturales en dos clases usando la relación "dos números están relacionados si dan el mismo resto al dividirlos por dos". Esta relación divide los números en dos grupos: los pares y los impares. Así, 4 y 8 son "equivalentes" porque ambos son números pares, pero 16 y 17 no son equivalentes porque uno es par y el otro es impar.
Para que una relación sea de equivalencia, debe cumplir tres reglas:
- Reflexiva: Cualquier elemento es equivalente a sí mismo. Por ejemplo, 5 es equivalente a 5.
- Simétrica: Si un elemento es equivalente a otro, entonces el segundo también es equivalente al primero. Si 5 es equivalente a 7, entonces 7 es equivalente a 5.
- Transitiva: Si un elemento es equivalente a un segundo, y ese segundo es equivalente a un tercero, entonces el primer elemento es equivalente al tercero. Si 5 es equivalente a 7, y 7 es equivalente a 9, entonces 5 es equivalente a 9.
La relación opuesta a la igualdad es la diferencia, que se representa con un signo igual tachado: 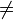 .
.
Galería de imágenes
Véase también
 En inglés: Equality (mathematics) Facts for Kids
En inglés: Equality (mathematics) Facts for Kids