Ecuación diofántica para niños

Una ecuación diofántica es un tipo especial de ecuación algebraica. Imagina que tienes una ecuación con dos o más letras (llamadas incógnitas), como x e y. La característica principal de una ecuación diofántica es que solo buscamos soluciones que sean números enteros (como -3, 0, 5) o números naturales (como 1, 2, 3). Además, los números que acompañan a las letras (los coeficientes) también deben ser enteros.
Un ejemplo sencillo de ecuación diofántica lineal (de primer grado) es 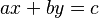 . Aquí, a, b y c son números enteros. Para que esta ecuación tenga soluciones enteras, hay una regla importante: el máximo común divisor de a y b debe poder dividir a c. Si esto se cumple, ¡la ecuación tendrá infinitas soluciones!
. Aquí, a, b y c son números enteros. Para que esta ecuación tenga soluciones enteras, hay una regla importante: el máximo común divisor de a y b debe poder dividir a c. Si esto se cumple, ¡la ecuación tendrá infinitas soluciones!
El nombre "diofántica" viene de Diofanto de Alejandría, un matemático griego que vivió hace mucho tiempo (en el siglo III). Él fue uno de los primeros en estudiar este tipo de ecuaciones y en usar símbolos en el álgebra. El estudio de estos problemas se llama hoy en día análisis diofántico.
Contenido
¿Qué es una Ecuación Diofántica?
Las ecuaciones diofánticas son como rompecabezas matemáticos donde solo aceptamos números enteros como respuestas. Esto las hace diferentes de otras ecuaciones donde las soluciones pueden ser cualquier tipo de número, como decimales o fracciones.
Ejemplos de Ecuaciones Diofánticas
Un ejemplo muy simple es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + y = 5 . Si no tuviéramos restricciones, esta ecuación tendría muchísimas soluciones (por ejemplo, x=2.5, y=2.5). Pero como es una ecuación diofántica, solo buscamos soluciones enteras. Si además pedimos que x e y sean números enteros positivos, las soluciones posibles son:
- (1, 4)
- (2, 3)
- (3, 2)
- (4, 1)
Un problema famoso que se resuelve con ecuaciones diofánticas es el del mono y los cocos, que es un desafío divertido para pensar.
Aquí te mostramos algunos tipos interesantes de ecuaciones diofánticas:
| Forma de la ecuación | Comentarios |
|---|---|
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax+by = c | Esta es la ecuación diofántica lineal, la más sencilla. |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): w^3 + x^3 = y^3 + z^3 | Una solución famosa es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 12^3 + 1^3 = 9^3 + 10^3 = 1729 . Este número es especial y se conoce como Número taxicab. |
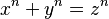 |
Si  , hay infinitas soluciones llamadas terna pitagórica. Pero si n es un número entero mayor que 2, el El último teorema de Fermat dice que no hay soluciones enteras positivas. Esto fue un gran misterio por siglos hasta que se demostró en 1995. , hay infinitas soluciones llamadas terna pitagórica. Pero si n es un número entero mayor que 2, el El último teorema de Fermat dice que no hay soluciones enteras positivas. Esto fue un gran misterio por siglos hasta que se demostró en 1995. |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 - ny^2 = \pm 1 | Esta es la ecuación de Pell, estudiada por matemáticos antiguos y modernos. |
Ecuaciones Diofánticas Lineales
Una ecuación diofántica lineal tiene la forma 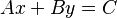 . Como mencionamos, solo tiene soluciones si el máximo común divisor de A y B divide a C. Si esto ocurre, ¡hay infinitas soluciones!
. Como mencionamos, solo tiene soluciones si el máximo común divisor de A y B divide a C. Si esto ocurre, ¡hay infinitas soluciones!
¿Cómo se encuentran las soluciones?
Para encontrar todas las soluciones de una ecuación como 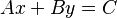 , primero necesitamos encontrar una solución particular (un par de números x e y que funcionen). Para esto, se usa un método llamado algoritmo de Euclides.
, primero necesitamos encontrar una solución particular (un par de números x e y que funcionen). Para esto, se usa un método llamado algoritmo de Euclides.
Una vez que tenemos una solución particular (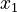 ,
, 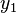 ), todas las demás soluciones se pueden encontrar con estas fórmulas:
), todas las demás soluciones se pueden encontrar con estas fórmulas:
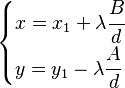
Aquí, 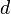 es el máximo común divisor de A y B, y
es el máximo común divisor de A y B, y  (lambda) puede ser cualquier número entero (0, 1, -1, 2, -2, etc.). Esto significa que hay muchísimas soluciones.
(lambda) puede ser cualquier número entero (0, 1, -1, 2, -2, etc.). Esto significa que hay muchísimas soluciones.
Un ejemplo práctico
Vamos a resolver 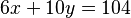 :
:
- Primero, calculamos el máximo común divisor de 6 y 10. Es 2.
- Como 2 divide a 104 (104 dividido por 2 es 52), sabemos que hay soluciones.
- Una solución particular para
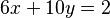 es
es 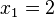 e
e  .
. - Para nuestra ecuación original (
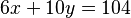 ), multiplicamos esa solución particular por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{104}{2} = 52 . Así, una solución particular para
), multiplicamos esa solución particular por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{104}{2} = 52 . Así, una solución particular para 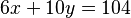 es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_1 = 2 \cdot 52 = 104 e Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_1 = -1 \cdot 52 = -52 .
es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_1 = 2 \cdot 52 = 104 e Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_1 = -1 \cdot 52 = -52 . - Finalmente, la solución general es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left\{\begin{array}{rccl} x &=& 104 &+ \lambda \cdot \frac{10}{2} \\ y &=& -52 &- \lambda \cdot \frac{6}{2}\end{array}\right. \forall \lambda \in \mathbb{Z}
Esto se simplifica a:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left\{\begin{array}{rccl} x &=& 104 &+ 5\lambda \\ y &=& -52 &- 3\lambda\end{array}\right. \forall \lambda \in \mathbb{Z}
Puedes probar con diferentes valores de  para encontrar soluciones. Por ejemplo, si
para encontrar soluciones. Por ejemplo, si  , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x=104, y=-52 . Si
, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x=104, y=-52 . Si  , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x=109, y=-55 .
, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x=109, y=-55 .
Solución con Aritmética Modular
También se pueden resolver ecuaciones diofánticas usando la aritmética modular, que es una forma de hacer cálculos con "restos". Por ejemplo, si tenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3x + 7y = 1 : 1. Podemos escribirla como una congruencia: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3x \equiv 1 \pmod{7} . Esto significa que cuando 3x se divide por 7, el resto es 1. 2. Buscamos un número que, al sumarle o restarle múltiplos de 7 a 1, sea divisible por 3. En este caso, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 + 2 \cdot 7 = 15 . Así, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3x \equiv 15 \pmod{7} . 3. Dividimos todo por 3: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x \equiv 5 \pmod{7} . 4. Esto significa que x puede ser 5, 12, 19, etc. (o -2, -9, etc.). El valor más pequeño y positivo para x es 5. 5. Ahora que sabemos que  , lo sustituimos en la ecuación original para encontrar y: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3(5) + 7y = 1 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 15 + 7y = 1 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 7y = 1 - 15 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 7y = -14 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = -2 ¡Así, (5, -2) es una solución!
, lo sustituimos en la ecuación original para encontrar y: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3(5) + 7y = 1 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 15 + 7y = 1 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 7y = 1 - 15 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 7y = -14 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = -2 ¡Así, (5, -2) es una solución!
Ecuación Pitagórica
Una ecuación diofántica muy famosa es la ecuación pitagórica: 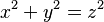 . Esta ecuación se relaciona con el Teorema de Pitágoras y los triángulos rectángulos. Las soluciones enteras (x, y, z) se llaman ternas pitagóricas. Por ejemplo, (3, 4, 5) es una terna pitagórica porque
. Esta ecuación se relaciona con el Teorema de Pitágoras y los triángulos rectángulos. Las soluciones enteras (x, y, z) se llaman ternas pitagóricas. Por ejemplo, (3, 4, 5) es una terna pitagórica porque 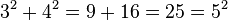 .
.
Si (x, y, z) es una terna pitagórica, también lo serán:
- (y, x, z) (cambiando el orden de x e y).
- (kx, ky, kz) (multiplicando por cualquier número entero k).
- Ternas con signos cambiados, como (-x, y, z).
Una terna es "primitiva" si los números x, y, z no tienen ningún divisor común aparte del 1. Todas las ternas primitivas se pueden generar con estas fórmulas:
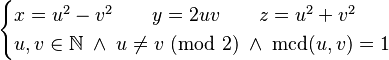
Donde u y v son números naturales, uno es par y el otro impar, y no tienen divisores comunes.
Aporte de Platón
El filósofo griego Platón también se interesó en las ternas pitagóricas. Él propuso una forma de encontrar los lados de un triángulo rectángulo en números enteros: 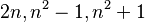 . Esto fue muy importante para el desarrollo de las matemáticas.
. Esto fue muy importante para el desarrollo de las matemáticas.
Ejemplos de Ternas Pitagóricas
Algunas ternas pitagóricas famosas son:
- (3, 4, 5)
- (7, 24, 25)
- (9, 40, 41)
El Décimo Problema de Hilbert
En el año 1900, un matemático llamado David Hilbert propuso una lista de 23 problemas muy difíciles que, si se resolvían, harían avanzar mucho las matemáticas. Uno de ellos, el décimo problema, trataba sobre las ecuaciones diofánticas. La pregunta era si existía un método general para saber si una ecuación diofántica tenía soluciones y cuántas.
Este problema fue resuelto en 1970 por el matemático Yuri Matiyasevich. Su teorema de Matiyasevich demostró que no existe un método general que pueda decirnos siempre si una ecuación diofántica tiene soluciones o cuántas. ¡Fue un descubrimiento muy importante!
Véase también
 En inglés: Diophantine equation Facts for Kids
En inglés: Diophantine equation Facts for Kids

