Bidimensional para niños
El espacio bidimensional o segunda dimensión es una forma de ver el espacio que solo tiene dos medidas: ancho y largo. Imagina una hoja de papel o la pantalla de tu tablet; tienen ancho y largo, pero no tienen profundidad. Los objetos que solo tienen estas dos medidas se llaman bidimensionales.
En matemáticas, un plano es un ejemplo de espacio bidimensional. En un plano, solo puedes encontrar figuras que también son bidimensionales, como un cuadrado o un círculo, o figuras unidimensionales, como una línea.
Contenido
¿Qué es el Espacio Bidimensional?
El espacio bidimensional es como una superficie plana infinita. No tiene grosor. Piensa en un mapa: puedes medir distancias a lo largo y a lo ancho, pero no puedes medir "hacia arriba" o "hacia abajo" en el mapa mismo. Es un concepto fundamental en muchas áreas de las matemáticas y la ciencia.
La Historia del Espacio 2D
La idea de entender el espacio bidimensional no es nueva. Desde hace mucho tiempo, los matemáticos han estudiado cómo se comportan las figuras en un plano.
Euclides y los Elementos
Hace más de 2000 años, un matemático griego llamado Euclides escribió una serie de libros llamados Elementos. En ellos, explicó muchas ideas sobre la geometría bidimensional. Habló de cómo las formas son similares, del famoso teorema de Pitágoras (que ayuda a calcular lados de triángulos), de la igualdad de ángulos y áreas, y de las líneas paralelas. Sus ideas son la base de la geometría que aprendemos hoy.
El Sistema de Coordenadas Cartesianas
Más tarde, en 1637, el filósofo y matemático René Descartes y, de forma independiente, Pierre de Fermat, tuvieron una idea brillante. Crearon un sistema para ubicar cualquier punto en un plano usando números. Este sistema se llama sistema de coordenadas cartesianas.
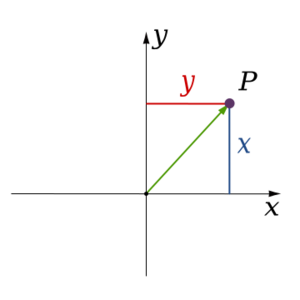
Funciona así: tienes dos líneas rectas que se cruzan en un punto central llamado origen (generalmente el punto (0,0)). Una línea va de lado a lado (el eje X) y la otra va de arriba abajo (el eje Y). Para encontrar un punto, solo necesitas dos números: uno que te dice qué tan lejos está a lo largo del eje X y otro que te dice qué tan lejos está a lo largo del eje Y. Es como usar una cuadrícula para encontrar un lugar en un mapa.
El Plano Complejo
Con el tiempo, los matemáticos descubrieron que el plano bidimensional podía usarse para representar números especiales llamados "números complejos". Este concepto dio origen al plano complejo, también conocido como plano de Argand, en honor a Jean-Robert Argand, aunque Caspar Wessel lo describió primero. Este plano es muy útil en áreas avanzadas de las matemáticas y la ingeniería.
Ejemplos de Figuras Bidimensionales
Hay muchas figuras que son bidimensionales. Aquí tienes algunos ejemplos:
- Todos los polígonos:
* Triángulos * Cuadrados, rectángulos, rombos, trapecios * Pentágonos * Hexágonos
- Otras figuras:
* Círculos * Elipses * Cualquier figura que pueda dibujarse completamente en una superficie plana. * Hojas de papel o de árboles.
Cómo se Ubican Puntos en 2D
Para describir la posición de un punto en un espacio bidimensional, usamos sistemas de coordenadas. Los más comunes son:
Coordenadas Cartesianas
Este es el sistema que ya mencionamos, con los ejes X e Y. Es muy usado en matemáticas y ciencias.
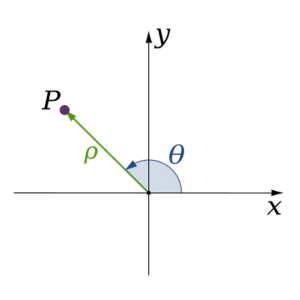
Coordenadas Polares
Este sistema usa una distancia desde un punto central (el origen) y un ángulo. Es como decir "ve 5 metros en esta dirección" en lugar de "ve 3 metros a la derecha y 4 metros hacia arriba".
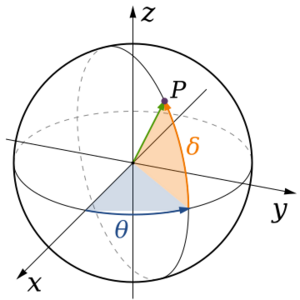
Coordenadas Geográficas
Aunque la Tierra es tridimensional, para ubicar lugares en su superficie usamos un sistema bidimensional: la latitud y la longitud. Es como un mapa gigante.
El Espacio 2D en la Ciencia
El concepto de espacio bidimensional es importante en varias ciencias:
- En la química, a veces se habla de sistemas bidimensionales cuando los átomos se unen muy fuertemente en dos direcciones, formando capas, pero más débilmente en la tercera. Un ejemplo es el grafito, que forma láminas muy delgadas.
- En la electricidad, un material puede ser un conductor bidimensional si la electricidad fluye muy bien en dos direcciones, pero casi nada en la tercera.
¿Qué es un Plano Proyectivo?
Un plano proyectivo es una idea matemática que expande el concepto de un plano normal. En un plano normal, las líneas paralelas nunca se cruzan. Pero en un plano proyectivo, se añaden "puntos en el infinito" donde estas líneas paralelas se encontrarían. Así, en un plano proyectivo, ¡todas las líneas se cruzan en algún punto! Los artistas del Renacimiento, al desarrollar la perspectiva en sus dibujos, sentaron las bases para esta idea matemática.
Representar 3D en 2D
Aunque el papel o la pantalla son bidimensionales, los artistas y diseñadores pueden crear la ilusión de profundidad y representar objetos tridimensionales. Esto se logra usando técnicas como la perspectiva, que hace que los objetos lejanos parezcan más pequeños y las líneas paralelas parezcan unirse en un punto. La computación gráfica 2D también utiliza estas ideas para crear imágenes que parecen tener profundidad.
El Espacio 2D en el Arte
El número de dimensiones también ayuda a clasificar las artes:
- Algunas artes se desarrollan en una sola dimensión, como la música (que se extiende en el tiempo).
- Otras se extienden en dos dimensiones, como la pintura o el dibujo.
- Y otras en tres dimensiones, como la escultura o la danza.
La perspectiva en el arte busca sugerir un espacio tridimensional en una obra bidimensional. Desde el Renacimiento, la perspectiva se ha combinado con las matemáticas. Hoy en día, las computadoras hacen que los cálculos para crear estas ilusiones sean mucho más fáciles.
Galería de imágenes
Véase también
 En inglés: 2D Facts for Kids
En inglés: 2D Facts for Kids
- Tridimensional
- Computación gráfica 2D
- Área
- Geometría descriptiva