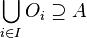Espacio compacto para niños
En el mundo de las matemáticas, específicamente en una rama llamada topología, un espacio compacto es como un conjunto especial de puntos que se comporta de manera similar a un conjunto finito. Imagina que tienes una lista infinita de números o puntos dentro de este espacio; la idea es que siempre podrás encontrar una parte de esa lista que se "acerque" cada vez más a un punto específico dentro del mismo espacio.
La compacidad es una propiedad que nos ayuda a entender mejor estos espacios. Un conjunto compacto es una parte de un espacio más grande que, por sí misma, también tiene esta propiedad de compacidad.
Piensa en la compacidad como una forma de describir un espacio que no tiene "agujeros" o "bordes faltantes". Es decir, incluye todos los puntos a los que otras secuencias de puntos se acercarían mucho. Por ejemplo, el intervalo abierto (0,1) no es compacto porque le faltan los puntos 0 y 1 en sus extremos. En cambio, el intervalo cerrado [0,1] sí es compacto porque incluye esos puntos.
De manera similar, el conjunto de los números racionales (fracciones) no es compacto porque tiene muchos "agujeros" donde deberían estar los números irracionales (como pi o la raíz cuadrada de 2). La línea de los números reales tampoco es compacta porque se extiende infinitamente en ambas direcciones. Sin embargo, si añadimos los puntos de "infinito positivo" y "infinito negativo" a la línea real, entonces sí se vuelve compacta.
Una forma de entender la compacidad es que si tomas una secuencia infinita de puntos de un espacio compacto, siempre podrás encontrar una parte de esa secuencia que se acerque a un punto dentro de ese mismo espacio.
El teorema de Bolzano-Weierstrass nos dice que, en el espacio euclidiano (como la línea numérica o el plano), un conjunto es compacto si está "cerrado" (incluye sus bordes) y "acotado" (no se extiende infinitamente).
Por ejemplo, si eliges un número infinito de puntos en el intervalo [0, 1], algunos de esos puntos se acercarán mucho a algún número real dentro de ese intervalo. Si los puntos se acercaran a 0 o 1, y estos no estuvieran incluidos en el intervalo (como en el caso de (0,1)), entonces el intervalo no sería compacto.
Contenido
Historia de la Compacidad
Primeras Ideas de Compacidad
En el siglo XIX, los matemáticos comenzaron a notar varias propiedades interesantes que más tarde se agruparían bajo el concepto de compacidad. Por ejemplo, Bernard Bolzano (en 1817) descubrió que cualquier secuencia de puntos que no se extiende infinitamente (es decir, está "acotada") siempre tiene una parte que se acerca a un punto específico, al que llamó "punto límite".
Bolzano usó un método llamado "bisección": dividía un intervalo a la mitad una y otra vez, siempre eligiendo la mitad que contenía infinitos puntos de la secuencia, hasta que llegaba al punto límite deseado. El significado completo de este descubrimiento no se entendió hasta casi 50 años después, cuando Karl Weierstrass lo redescubrió.
Compacidad en Espacios de Funciones
En la década de 1880, se vio que ideas similares al teorema de Bolzano-Weierstrass podían aplicarse a "espacios de funciones", no solo a números o puntos geométricos. Esto significa que las funciones podían ser vistas como "puntos" en un espacio más grande. Las investigaciones de Giulio Ascoli y Cesare Arzelà llevaron al teorema de Arzelà-Ascoli, que es una versión más general del teorema de Bolzano-Weierstrass para familias de funciones continuas. Este teorema decía que de una familia adecuada de funciones, se podía extraer una secuencia de funciones que se acercaba uniformemente a una función límite.
A principios del siglo XX, David Hilbert y Erhard Schmidt encontraron resultados parecidos al estudiar las ecuaciones integrales. Esto llevó a la idea de un "operador compacto", que es una parte de la noción general de espacio compacto. Finalmente, Maurice Fréchet fue quien, en 1906, usó el término "compacidad" para describir este fenómeno general.
La Noción de Recubrimientos Abiertos
Al mismo tiempo, a finales del siglo XIX, surgió otra idea de compacidad. En 1870, Eduard Heine demostró que una función continua en un intervalo cerrado y acotado era "uniformemente continua". Para probar esto, usó un concepto clave: si cubres un intervalo con muchos intervalos abiertos más pequeños, siempre puedes elegir un número finito de esos intervalos pequeños que aún cubran el original.
La importancia de esta idea fue reconocida por Émile Borel (1895) y generalizada por Pierre Cousin (1895) y Henri Lebesgue (1904). Este resultado se conoce como el teorema de Heine-Borel y es otra propiedad especial de los conjuntos cerrados y acotados de números reales.
Esta propiedad era muy importante porque permitía pasar de información "local" (sobre una pequeña parte de un conjunto) a información "global" (sobre todo el conjunto). Finalmente, los matemáticos Pavel Alexandrov y Pavel Urysohn formularon la compacidad de Heine-Borel de una manera que podía aplicarse a la noción moderna de espacio topológico. Esta última noción de compacidad, basada en "recubrimientos finitos", se convirtió en la más usada porque era más robusta y podía aplicarse en un entorno más general.
¿Qué es un Recubrimiento Abierto?
Para entender la compacidad moderna, primero necesitamos saber qué es un "recubrimiento abierto":
|
Si tienes un recubrimiento de un conjunto A, un subrecubrimiento es una parte de esa colección original que, por sí misma, también cubre a A.
La definición de compacidad es entonces:
|
Ejemplos de Compacidad
- El conjunto K = {1, 1/2, 1/3, 1/4,..., 0} es compacto. Si tomas un "vecindario" alrededor de 0, este incluirá a casi todos los números 1/n (excepto unos pocos). Así, si cubres K con conjuntos abiertos, puedes elegir un conjunto que contenga a 0 y solo unos pocos conjuntos más para cubrir los puntos restantes, haciendo que el subrecubrimiento sea finito.
- El intervalo abierto (0, 1) no es compacto. Imagina que lo cubres con los intervalos (0, 1 − 1/n) para diferentes valores de n (por ejemplo, (0, 0.5), (0, 0.6), (0, 0.7), etc.). No importa cuántos de estos intervalos elijas, siempre habrá un punto en (0,1) que no estará cubierto por tu selección finita.
Compacidad en Espacios Métricos
En un espacio métrico (donde puedes medir distancias entre puntos), como el espacio euclídeo (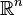
), un conjunto es compacto si y solo si es "cerrado" (incluye sus bordes) y "acotado" (no se extiende infinitamente). Esto es muy útil para saber si un conjunto es compacto en estos espacios.
Teoremas Importantes Relacionados con la Compacidad
Teorema de Heine-Borel
Este teorema es fundamental. Dice que un subconjunto del espacio euclídeo es compacto si y solo si es cerrado y acotado. Esto simplifica mucho la verificación de la compacidad en estos espacios.
Teorema de la Compactificación de Alexándrov
Este teorema nos permite tomar un espacio topológico y añadirle un solo punto, llamado "punto del infinito", para que el espacio resultante se vuelva compacto. Esto es útil para estudiar propiedades de espacios que no son compactos por sí mismos.
Teorema de Tíjonov
Este teorema es muy poderoso. Dice que si tienes una colección de espacios compactos, no importa si son finitos o infinitos, el "producto" de todos ellos (es decir, un nuevo espacio formado por combinaciones de puntos de cada uno) también será compacto. Para demostrar esto, se necesita una herramienta matemática avanzada llamada el axioma de elección.
Teorema de Arzelà-Ascoli
Este teorema es una herramienta clave en el análisis matemático. Nos ayuda a decidir si un conjunto de funciones continuas es compacto. Es como una extensión del teorema de Heine-Borel, pero para funciones. Nos dice que un conjunto de funciones continuas es compacto si, además de estar cerrado y acotado, cumple una condición extra llamada "equicontinuidad".
Galería de imágenes
-
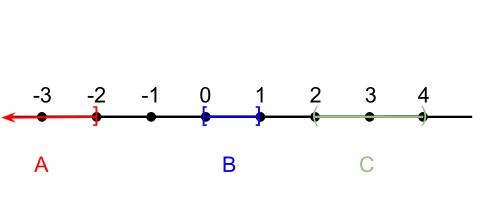
De acuerdo al criterio de compacidad para el espacio Euclidiano como es enunciado por el teorema de Heine–Borel, el intervalo A Plantilla:= (−∞, −2] no es compacto porque no es acotado. El intervalo C Plantilla:= (2, 4) no es compacto porque no es cerrado. El intervalo B Plantilla:= [0, 1] es compacto porque es cerrado y acotado.
Véase también
En inglés: Compact space Facts for Kids
