Conjetura de Collatz para niños
La conjetura de Collatz es un famoso problema matemático que fue propuesto por el matemático Lothar Collatz en 1937. También se le conoce como la conjetura 3n+1 o la conjetura de Ulam. A pesar de que muchos matemáticos han intentado resolverla, ¡todavía no se ha encontrado una respuesta definitiva!
Contenido
¿Qué es la Conjetura de Collatz?
La conjetura de Collatz propone una serie de pasos para cualquier número entero positivo. Imagina que tienes un número y le aplicas estas reglas:
- Si el número es par, lo divides entre 2.
- Si el número es impar, lo multiplicas por 3 y luego le sumas 1.
La conjetura dice que, si repites estos pasos una y otra vez, ¡siempre llegarás al número 1, sin importar con qué número positivo empieces!
¿Cómo funciona la secuencia de Collatz?
Para entenderlo mejor, vamos a ver cómo se forma una secuencia. Empiezas con un número, aplicas la regla que le corresponde (par o impar), y el resultado se convierte en el nuevo número para el siguiente paso. Así sigues hasta ver si llegas al 1.
Por ejemplo, si empezamos con el número 13:
- 13 es impar, así que: 13 × 3 + 1 = 40
- 40 es par, así que: 40 ÷ 2 = 20
- 20 es par, así que: 20 ÷ 2 = 10
- 10 es par, así que: 10 ÷ 2 = 5
- 5 es impar, así que: 5 × 3 + 1 = 16
- 16 es par, así que: 16 ÷ 2 = 8
- 8 es par, así que: 8 ÷ 2 = 4
- 4 es par, así que: 4 ÷ 2 = 2
- 2 es par, así que: 2 ÷ 2 = 1
¡Llegamos al 1! La secuencia completa para el 13 es: 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
Ejemplos de secuencias
Veamos otros ejemplos para entender mejor cómo se comportan los números:
- Si empiezas con 6, la secuencia es: 6, 3, 10, 5, 16, 8, 4, 2, 1. (8 pasos)
- Si empiezas con 11, la secuencia es: 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. (14 pasos)
- Si empiezas con 27, la secuencia es mucho más larga. Tiene 111 pasos y el número más grande que alcanza es 9232 antes de bajar hasta 1.
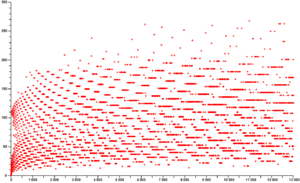
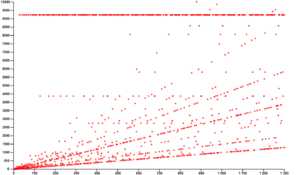
Los matemáticos han probado esta conjetura con números muy grandes usando computadoras. Hasta mayo de 2020, se ha verificado que la conjetura se cumple para todos los números menores que 2 elevado a la potencia de 68 (un número gigantesco). Esto no demuestra que sea cierta para todos los números, pero sí es una evidencia muy fuerte.
¿Por qué es tan difícil de resolver?
La conjetura de Collatz es un problema abierto en matemáticas, lo que significa que nadie ha podido demostrar si es verdadera para todos los números o si existe algún número que no llegue al 1.
Si existiera un número que no llegara al 1, podría pasar una de estas dos cosas:
- La secuencia del número seguiría creciendo sin límite, sin volver nunca a bajar.
- La secuencia del número entraría en un ciclo que no incluye el 1 (por ejemplo, 4, 2, 1 es un ciclo, pero la conjetura dice que todos los números deben llegar a este ciclo).
Hasta ahora, no se ha encontrado ningún número que haga esto.
Propiedades interesantes
Los matemáticos han descubierto algunas propiedades curiosas de estas secuencias:
Números que son sumas de potencias de 4
Algunos números, como 5 (que es 1 + 4), 21 (que es 1 + 4 + 16), o 85 (que es 1 + 4 + 16 + 64), llegan al 1 de una manera muy directa. Por ejemplo, si tomas 21, al multiplicarlo por 3 y sumarle 1, obtienes 64. Y 64 es una potencia de 2 (2x2x2x2x2x2), así que al dividirlo varias veces entre 2, ¡rápidamente llegas al 1!
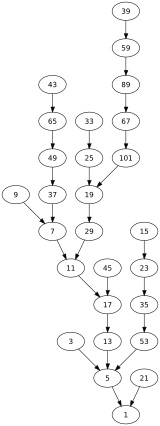
Cómo se unen las secuencias
A veces, las secuencias de dos números diferentes se encuentran en un punto y luego siguen el mismo camino hasta el 1.
- Por ejemplo, la secuencia del 7 es: 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
- La secuencia del 15 es: 15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1.
Como puedes ver, ambas secuencias se unen en el número 40 y luego siguen el mismo camino.
Variantes de la conjetura
Existen otras conjeturas similares a la de Collatz. Por ejemplo, la "conjetura 2n+2" es parecida, pero cambia la regla para los números impares: si el número es impar, se multiplica por 2 y se le suma 2.
¿Se puede programar la conjetura?
Sí, es posible escribir programas de computadora para calcular las secuencias de Collatz. Aquí te mostramos un ejemplo sencillo en el lenguaje de programación python:
# Definir una función que aplica la operación de la conjetura
def collatz(n):
if n % 2 == 0: # Si el número es par, se divide entre 2
return n // 2
else: # Si el número es impar, se multiplica por 3 y se suma 1
return 3 * n + 1
# Pedir al usuario que ingrese un número entero positivo
n = int(input("Ingrese un número entero positivo: "))
# Mientras el número no sea 1, aplicar la función y mostrar el resultado
while n != 1:
n = collatz(n)
print(n)Galería de imágenes
-
Tiempo de órbita (número de pasos o iteraciones) necesario para alcanzar la unidad para números comprendidos entre 1 y 13000.
-
Cota superior para valores entre 1 y 1300. La línea horizontal superior corresponde a la cota 9232. Esta cota es un valor 'preferido' para muchas secuencias, como las que comienzan con 27, 31, 41, 47, 54, 55, 62, 63, etc.
Véase también
En inglés: Collatz conjecture Facts for Kids
