Arquitas para niños
Arquitas de Tarento (nacido alrededor del 430 a.C. y fallecido cerca del 360 a.C.) fue un pensador muy importante de la antigua Grecia. Fue un filósofo, matemático, astrónomo, estadista (una persona que dirige el gobierno) y general militar. Vivió en la misma época que el famoso filósofo Platón.
Arquitas trabajó en su ciudad natal, Tarento, que era una colonia griega en lo que hoy es el sur de Italia. Como filósofo, formó parte de la escuela de los pitagóricos, que seguían las ideas de Pitágoras. Es conocido por su amistad con Platón, por una "paloma voladora" que se dice que inventó y por un experimento mental con el que imaginó que el universo era infinito. Solo se conservan algunos escritos suyos, que tratan principalmente sobre matemáticas y música.
Arquitas creía que el conocimiento científico era fácil de conseguir si se usaba el método correcto. Para él, las matemáticas eran la ciencia más importante. Su mayor logro en matemáticas fue resolver el problema de cómo duplicar el cubo, lo que muestra lo avanzado que era para su tiempo. También contribuyó a la teoría musical con sus ideas matemáticas sobre los intervalos armónicos. En el estudio de la luz (óptica), intentó explicar cómo se refleja la luz, y en el estudio del sonido (acústica), cómo se producen los diferentes tonos. Sus descubrimientos fueron muy valorados en la antigüedad y por los historiadores modernos.
Además de sus estudios, Arquitas fue un líder político y militar clave en Tarento y en una unión de ciudades griegas en el sur de Italia. Sus éxitos en la guerra le dieron mucho respeto. En su ciudad, buscó el equilibrio entre las personas, creyendo que la justicia podía explicarse con la ciencia para lograr la paz social.
Contenido
¿Quién fue Arquitas de Tarento?
Arquitas nació en Tarento, una ciudad en la región de la Magna Grecia (hoy parte de Italia), entre los años 435 y 410 a.C. Fue hijo de Hestieo o de Mneságoras. Fue un líder militar en tres guerras y fue elegido strategos (un tipo de general y gobernante) de Tarento durante siete años. Esto era muy inusual, ya que la ley normalmente prohibía ser reelegido por más de un año, lo que demuestra su gran prestigio.
Arquitas impulsó cambios importantes en Tarento, ayudando a que se convirtiera en una de las ciudades más ricas y pobladas de la Magna Grecia. Mejoró la ciudad construyendo monumentos, templos y otros edificios. También impulsó el comercio, buscando acuerdos con otras regiones como Istria, Grecia y África.
La conexión de Arquitas con los pitagóricos y Platón
Arquitas perteneció a la escuela de los Pitagóricos, y fue alumno de Filolao. Fue un buen amigo de Platón, a quien conoció cuando Platón viajó al sur de Italia y a Sicilia en el año 388/387 a.C., después de la muerte de Sócrates. En una de sus cartas, Platón cuenta que Arquitas lo ayudó cuando tuvo problemas con Dionisio II de Siracusa, enviándole una carta de recomendación y un barco a Sicilia en el 361 a.C. Algunos historiadores creen que Arquitas fue maestro de Platón en temas pitagóricos, mientras que otros piensan que fue su alumno.
Arquitas enseñó matemáticas a Eudoxo de Cnidos y fue maestro de Menecmo. Fue una de las primeras personas en acercarse a resolver el problema de la Duplicación del cubo. También fue uno de los primeros, después de Pitágoras, en estudiar juntos la Aritmética, la Geometría, la Astronomía y la Música, lo que se conocía como el Quadrivium. También trabajó en Acústica. Se cree que inventó la polea, el tornillo y un tipo de mecanismo con alas, parecido a un pájaro, que podía volar unos 300 metros gracias a la fuerza del vapor. Según Aristóteles, Arquitas inventó el sonajero. Algunos también creen que influyó directamente en Euclides.
Según el poeta romano Horacio, Arquitas murió en un naufragio en las costas de Apulia entre los años 360 y 350 a.C. Horacio escribió que su cuerpo quedó sin sepultura en la orilla hasta que un navegante le echó arena encima, lo que era importante para que su alma pudiera descansar.
¿Qué ideas tenía Arquitas sobre el conocimiento?
Aunque Arquitas vivió después de Sócrates, se le considera parte de los Presocráticos porque sus ideas venían de una tradición más antigua, antes de la influencia de Sócrates. Sin embargo, esto es un poco complicado porque sus escritos son posteriores a la muerte de Sócrates.
Arquitas pensaba que la "ciencia de los números", a la que llamaba logistikē, era la base de todas las ciencias y más importante que la geometría. En esto coincidía con Platón, quien también valoraba mucho las matemáticas. Sin embargo, Platón veía las matemáticas como una preparación para la filosofía y se enfocaba en entender la realidad de forma puramente intelectual. Arquitas, en cambio, no despreciaba la experiencia práctica y no separaba tan estrictamente lo que se puede conocer con la mente de lo que se percibe con los sentidos.
Para Arquitas, la aritmética también era importante para la política. Creía que podía ayudar a encontrar formas justas y equilibradas de distribuir los bienes entre los ciudadanos. Como estas fórmulas podían ser verificadas por todos, Arquitas pensaba que podían establecer y mantener la paz social. Esto era muy importante en las ciudades griegas, que a menudo sufrían conflictos violentos. Arquitas buscaba el equilibrio entre las clases sociales para evitar estas luchas, esperando que un "cálculo" correcto asegurara que nadie se excediera.
La importancia de las matemáticas
Bruno Snell señala que la palabra máthema, que significa "lo que se aprende", empezó a usarse para referirse a la ciencia por primera vez con Arquitas. Para él, las matemáticas eran el centro del conocimiento. Además de la geometría y la aritmética, la astronomía y la música también eran parte de los mathémata. Arquitas llamaba a estas cuatro ciencias "hermanas". Más tarde, el significado de máthema se redujo solo a las matemáticas, porque se pensaba que solo ellas podían dar un conocimiento totalmente seguro.
Arquitas desarrolló una filosofía de la ciencia donde explicaba cómo buscar el conocimiento de forma adecuada. Era optimista sobre el conocimiento; creía que los descubrimientos eran fáciles si se tenía el método correcto. Aunque no se sabe mucho de los detalles de su método, se sabe que pensaba que primero había que entender bien la naturaleza de "todo", y luego se podía comprender mejor cada cosa individual. Así, el conocimiento científico avanzaba de lo más general a lo más específico. Arquitas estaba convencido de que descubrir las cosas por uno mismo era mejor que simplemente aprender lo que ya se sabía.
En cuanto a la ética, Arquitas insistía en que siempre se debía actuar con razón y nunca dejarse llevar por la ira o los deseos.
¿Qué pensaba Arquitas sobre el universo?
Se dice que Arquitas fue astrónomo, aunque esta información viene de poetas romanos que quizás no tenían datos muy precisos. Sin embargo, es muy famoso por su argumento sobre la infinitud del universo. Él propuso un experimento mental: si alguien llegara a un supuesto borde del universo y extendiera su mano o un palo, se encontraría con algo (otro cuerpo o espacio vacío), lo que significaría que el universo continúa. Por lo tanto, el universo debe ser infinito. Esta idea fue retomada por otros filósofos y científicos mucho después.
¿Cuáles fueron los aportes de Arquitas a las matemáticas?
Números irracionales
Arquitas estudió las relaciones matemáticas como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (n+1):n , que en su época se llamaban "superproporcionales". Estas son relaciones donde la diferencia entre dos números es una parte del segundo número. Arquitas demostró que "entre dos números en una relación superproporcional, nunca se pueden encontrar números intermedios que mantengan la misma proporción". En términos modernos, esto significa que existen números que no pueden expresarse como fracciones simples, es decir, números irracionales. Por ejemplo, la raíz cuadrada Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{(n+1):n} es irracional.
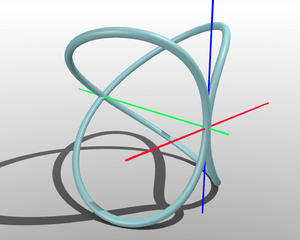
La Curva de Arquitas
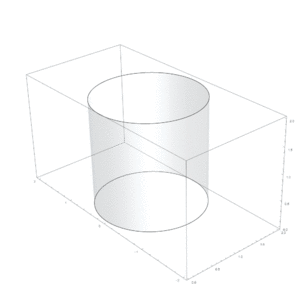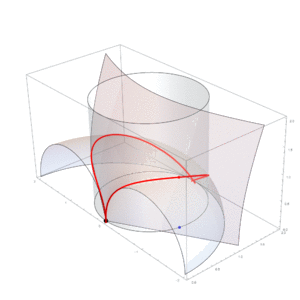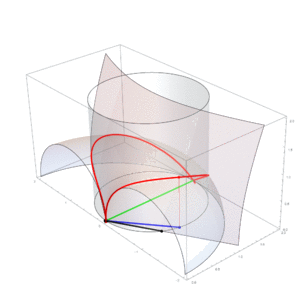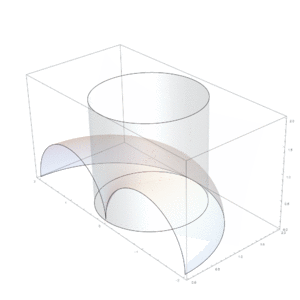
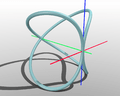
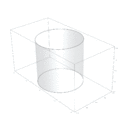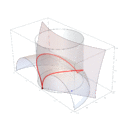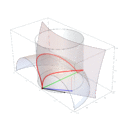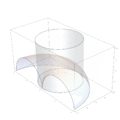
Un problema matemático muy antiguo era el de duplicar el cubo, es decir, construir un cubo que tuviera el doble de volumen que otro. Hipócrates de Quíos había simplificado este problema, pero no había logrado construir las distancias necesarias. Arquitas fue el primero en encontrar una solución usando una curva especial que lleva su nombre: la curva de Arquitas.
Esta curva es muy importante porque fue la primera curva en la historia de las matemáticas que no está contenida en un solo plano (es decir, es tridimensional). Para resolver el problema, Arquitas usó las superficies de tres figuras geométricas: un toro (como una rosquilla), un cilindro y un cono. La intersección de estas tres superficies le dio un punto clave que le permitió resolver el problema de duplicar el cubo. Esta forma de construir una solución es única para la matemática antigua y muy sorprendente para su época.
¿Qué cosas llevan el nombre de Arquitas?
- El cráter lunar Archytas fue nombrado en su honor.
- El asteroide (14995) Archytas también lleva su nombre.
Galería de imágenes
Véase también
 En inglés: Archytas Facts for Kids
En inglés: Archytas Facts for Kids