Cuadrilátero para niños
Datos para niños Cuadrilátero |
||
|---|---|---|
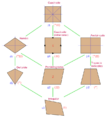
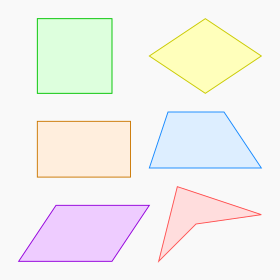 Varios tipos de cuadriláteros
|
||
| Características | ||
| Lados | 4 | |
| Vértices | 4 | |
| Símbolo de Schläfli | {4} (para el cuadrado) | |
| Área | varios métodos; véase artículo |
|
| Ángulo interior | 90° (para el cuadrado y el rectángulo) | |
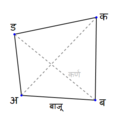
Un cuadrilátero es una figura geométrica plana que tiene cuatro lados y cuatro vértices (o esquinas). Es como un triángulo, pero con un lado y una esquina más.
La palabra "cuadrilátero" viene del latín "quadri", que significa "cuatro", y "latus", que significa "lado".
Los cuadriláteros pueden ser simples, lo que significa que sus lados no se cruzan. También pueden ser complejos o cruzados, donde sus lados sí se cruzan. Los cuadriláteros simples se dividen en convexos o cóncavos.
La suma de los ángulos interiores de cualquier cuadrilátero simple siempre es 360 grados. Esto es una regla importante en geometría.
Contenido
- Elementos clave de un cuadrilátero
- Tipos de cuadriláteros: una clasificación sencilla
- Cuadriláteros simples: convexos y cóncavos
- Cuadriláteros complejos o cruzados
- Simetría en los cuadriláteros
- Cómo calcular el área de un cuadrilátero
- Diagonales: propiedades y longitudes
- Bimedianas: conectando puntos medios
- Desigualdades importantes
- Galería de imágenes
- Véase también
Elementos clave de un cuadrilátero
Para entender bien un cuadrilátero, es útil conocer sus partes:
- Vértices: Son los cuatro puntos donde se unen los lados.
- Lados: Son los cuatro segmentos que conectan los vértices.
- Diagonales: Son los dos segmentos que unen vértices que no están uno al lado del otro.
- Ángulos interiores: Son los ángulos que se forman dentro de la figura por dos lados que se tocan.
- Ángulos exteriores: Son los ángulos que se forman fuera de la figura al extender uno de sus lados.
Tipos de cuadriláteros: una clasificación sencilla
Los cuadriláteros se clasifican según cómo son sus lados y sus ángulos. Aquí te presentamos los tipos más comunes:
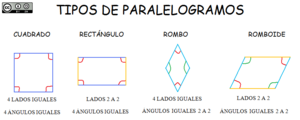
Paralelogramos: lados opuestos paralelos
Los paralelogramos son cuadriláteros donde los lados opuestos son paralelos entre sí. Dentro de los paralelogramos, encontramos:
- Cuadrado: Tiene los cuatro lados iguales y los cuatro ángulos rectos (de 90°). Sus diagonales son iguales y se cruzan formando un ángulo de 90°.
- Rombo: Tiene los cuatro lados iguales, pero sus ángulos no son necesariamente rectos. Sus diagonales son diferentes y se cruzan formando un ángulo de 90°.
- Rectángulo: Tiene los lados opuestos iguales y los cuatro ángulos rectos (de 90°). Sus diagonales son iguales, pero no se cruzan formando un ángulo de 90°.
- Romboide: Sus lados opuestos son iguales, pero sus ángulos no son rectos. Sus diagonales son de diferente longitud y no se cruzan formando un ángulo de 90°.
Trapecios: al menos un par de lados paralelos
Un trapecio es un cuadrilátero que tiene al menos un par de lados paralelos. Estos lados paralelos se llaman "bases".
- Trapecio isósceles: Es un trapecio donde los lados no paralelos tienen la misma longitud.
- Trapecio rectángulo: Es un trapecio que tiene un lado perpendicular a sus bases, formando ángulos rectos.
Trapezoides: sin lados paralelos
Un trapezoide es un cuadrilátero que no tiene ningún par de lados paralelos. Es el tipo más general de cuadrilátero convexo.
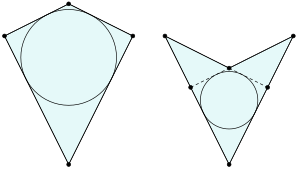
Deltoides: lados adyacentes iguales
Un deltoide (también conocido como cometa) tiene dos pares de lados adyacentes (que están uno al lado del otro) de igual longitud. Sus diagonales se cruzan formando un ángulo de 90°.
Cuadriláteros simples: convexos y cóncavos
Un cuadrilátero es simple si sus lados no se cruzan.
Cuadriláteros convexos
En un cuadrilátero convexo, todos los ángulos interiores son menores de 180°. Además, sus dos diagonales siempre se encuentran dentro de la figura. Los tipos de cuadriláteros que hemos visto (paralelogramos, trapecios, trapezoides, deltoides) son ejemplos de cuadriláteros convexos.
Cuadriláteros cóncavos
En un cuadrilátero cóncavo, al menos uno de sus ángulos interiores mide más de 180°. Esto hace que la figura tenga una "hendidura" o "curva hacia adentro". Una de sus diagonales se encuentra fuera de la figura.
- Un dardo (o punta de flecha) es un tipo de cuadrilátero cóncavo con simetría.
Cuadriláteros complejos o cruzados
Un cuadrilátero complejo o cruzado es aquel donde sus lados se cruzan entre sí. Se les puede llamar también "cuadrilátero mariposa" o "lazo de pajarita".
Simetría en los cuadriláteros
La simetría nos ayuda a clasificar los cuadriláteros:
Ejes de simetría
- 4 Ejes: El cuadrado tiene cuatro ejes de simetría. Puedes doblarlo por la mitad de cuatro maneras diferentes y que las dos partes coincidan.
- 2 Ejes: El rombo y el rectángulo tienen dos ejes de simetría.
- 1 Eje: El trapecio isósceles y el deltoide (tanto cóncavo como convexo) tienen un eje de simetría.
Simetría rotacional
- El cuadrado se ve igual si lo giras 90°.
- El rombo y el rectángulo se ven igual si los giras 180°.
Cómo calcular el área de un cuadrilátero
El área de un cuadrilátero es la medida de su superficie. Hay varias maneras de calcularla, dependiendo del tipo de cuadrilátero y la información que tengamos.
Área usando diagonales y ángulos
Una forma general de calcular el área de un cuadrilátero convexo es usando las longitudes de sus diagonales (p y q) y el ángulo (θ) que forman al cruzarse:
- K = (1/2) * p * q * sin(θ)
Si las diagonales se cruzan formando un ángulo de 90° (como en un rombo o un cuadrado), la fórmula se simplifica a:
- K = (1/2) * p * q
Área usando los lados y ángulos opuestos
La fórmula de Bretschneider es una forma más compleja que usa las longitudes de los lados (a, b, c, d), el semiperímetro (s, que es la mitad del perímetro) y dos ángulos opuestos (A y C):
- K = √((s-a)(s-b)(s-c)(s-d) - abcd * cos²((A+C)/2))
Si el cuadrilátero es cíclico (es decir, se puede dibujar una circunferencia que pase por sus cuatro vértices), esta fórmula se simplifica a la fórmula de Brahmagupta:
- K = √((s-a)(s-b)(s-c)(s-d))
Diagonales: propiedades y longitudes
Las diagonales son muy importantes en los cuadriláteros.
Propiedades de las diagonales
La forma en que las diagonales se cruzan y sus longitudes nos dicen mucho sobre el tipo de cuadrilátero:
| Cuadrilátero | Diagonales se bisecan (se cortan por la mitad) | Diagonales perpendiculares (se cruzan a 90°) | Diagonales iguales |
|---|---|---|---|
| Trapecio | No | No (generalmente) | No |
| Trapecio isósceles | No | No (generalmente) | Sí |
| Paralelogramo | Sí | No | No |
| Deltoide | Una biseca a la otra | Sí | No (generalmente) |
| Rectángulo | Sí | No | Sí |
| Rombo | Sí | Sí | No |
| Cuadrado | Sí | Sí | Sí |
Longitud de las diagonales
Podemos calcular la longitud de las diagonales usando el teorema del coseno en los triángulos que se forman dentro del cuadrilátero. Por ejemplo, para una diagonal p que une los vértices A y C, y los lados a, b, c, d:
- p = √(a² + b² - 2ab cos(B))
- q = √(a² + d² - 2ad cos(A))
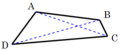
Bimedianas: conectando puntos medios
Las bimedianas de un cuadrilátero son los segmentos que unen los puntos medios de los lados opuestos. Se cruzan en el centroide de los vértices del cuadrilátero.
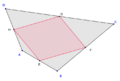
Un dato interesante es el Teorema de Varignon: si unes los puntos medios de los lados de cualquier cuadrilátero, la figura que se forma es siempre un paralelogramo. Este paralelogramo tiene propiedades especiales:
- Sus lados son paralelos a las diagonales del cuadrilátero original.
- Su área es la mitad del área del cuadrilátero original.
- Sus diagonales son las bimedianas del cuadrilátero original.
Desigualdades importantes
En geometría, las desigualdades nos ayudan a entender los límites de las formas.
Desigualdades de área
- El cuadrado es el cuadrilátero con mayor área para un perímetro dado.
- De todos los cuadriláteros con lados dados, el cuadrilátero cíclico (el que se puede inscribir en una circunferencia) tiene el área más grande.
- Si las diagonales de un cuadrilátero son perpendiculares, su área es la más grande posible para esas longitudes de diagonales.
Desigualdad de Ptolomeo
Para cualquier cuadrilátero convexo, el producto de sus diagonales (p * q) es menor o igual que la suma de los productos de sus lados opuestos (ac + bd).
- pq ≤ ac + bd
La igualdad solo se cumple si el cuadrilátero es cíclico.
Galería de imágenes
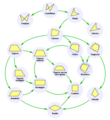
-
Diagrama de Euler de diversos tipos de cuadriláteros simples
-
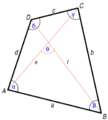
Los cuatro lados de un cuadrilátero: a, b, c, d ;
los cuatro vértices: A, B, C, D ;
las dos diagonales: e, f.
Véase también
 En inglés: Quadrilateral Facts for Kids
En inglés: Quadrilateral Facts for Kids