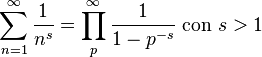Teoría analítica de números para niños
En el mundo de las matemáticas, la teoría analítica de números es una parte de la teoría de números. Usa herramientas del análisis matemático para resolver preguntas sobre los números enteros. Se dice que esta rama comenzó con Peter Gustav Lejeune Dirichlet, quien usó las funciones L de Dirichlet para demostrar el Teorema de Dirichlet sobre las progresiones aritméticas. Otro avance importante en este campo es el teorema de los números primos.
Contenido
Ramas principales de la teoría analítica de números
La teoría analítica de números se divide en dos grandes áreas. Estas se distinguen más por los problemas que estudian que por sus métodos:
¿Qué es la teoría multiplicativa de números?
La teoría multiplicativa de números se enfoca en cómo se distribuyen los números primos. Por ejemplo, busca estimar cuántos números primos hay en un rango específico. Incluye el teorema de los números primos y el teorema de Dirichlet sobre los primos en progresiones aritméticas.
¿Qué es la teoría aditiva de números?
La teoría aditiva de números estudia cómo se forman los números enteros al sumarlos. Un ejemplo es la conjetura de Goldbach, que dice que todo número par mayor que dos se puede escribir como la suma de dos números primos. Un resultado importante en esta área es la solución del problema de Waring.
Los avances en esta teoría a menudo mejoran las técnicas existentes. Esto ayuda a reducir errores y a aplicar los métodos a más problemas. Por ejemplo, el método del círculo de Hardy y Littlewood se ha vuelto muy útil.
Después de 1950, una gran novedad fue el desarrollo de los métodos de cribado. Son herramientas muy útiles para problemas multiplicativos. También surgió la teoría probabilística de números, que usa ideas de la teoría de la probabilidad para estimar cómo se distribuyen ciertas funciones de números.
Un desarrollo reciente notable es la demostración de Green y Tao. Ellos probaron la existencia de progresiones aritméticas de cualquier longitud en los números primos.
Problemas y resultados importantes
Los resultados más importantes de la teoría analítica de números no suelen ser reglas exactas sobre los números enteros. En cambio, son muy buenos para dar estimaciones y límites aproximados de varias funciones. Aquí tienes algunos ejemplos:
El famoso teorema de los números primos
El Teorema de los números primos es uno de los resultados más conocidos de esta teoría. Euclides demostró que hay infinitos números primos. Sin embargo, es muy difícil encontrar un método rápido para saber si un número grande es primo.
Un problema relacionado es saber cuántos números primos se espera que haya por debajo de un número grande N. Gauss pensó que este número es muy parecido a una integral específica.
En 1859, Bernhard Riemann usó el análisis complejo y una función especial, la función zeta de Riemann, para encontrar una fórmula para los números primos. La parte principal de la fórmula de Riemann era la misma integral que Gauss había sugerido. Riemann descubrió que los errores en esta fórmula están relacionados con los ceros complejos de la función zeta.
Usando las ideas de Riemann, Jacques Hadamard y Charles Jean de la Vallée-Poussin lograron demostrar la conjetura de Gauss. Ellos probaron que si π(x) es el número de primos menores o iguales a x, entonces:
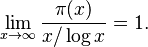
Este resultado se conoce como el Teorema de los números primos. En pocas palabras, dice que para un número N grande, la cantidad de primos menores o iguales a N es aproximadamente N dividido por el logaritmo de N.
También se puede preguntar cuántos números primos hay en una progresión aritmética (una secuencia de números que aumentan de forma constante). Dirichlet demostró que toda progresión aritmética con ciertos requisitos contiene infinitos primos.
Existe una conjetura compleja llamada la conjetura de los primos gemelos. Esta pregunta si hay infinitos pares de primos que están separados por solo 2 unidades (como 3 y 5, o 11 y 13).
El problema de Waring
Uno de los problemas más importantes en la teoría aditiva de números es el problema de Waring. Este pregunta si cualquier número entero positivo se puede escribir como la suma de un número limitado de potencias (por ejemplo, cuadrados o cubos).
Para los cuadrados (potencia 2), Lagrange lo resolvió en 1770. Demostró que todo número entero positivo es la suma de como máximo cuatro cuadrados. El caso general lo probó Hilbert en 1909. Más tarde, Hardy y Littlewood usaron técnicas analíticas para atacar el problema, desarrollando el método del círculo.
Problemas diofantinos
Los problemas diofantinos buscan soluciones enteras para ecuaciones que tienen polinomios. También se preguntan cuántas soluciones se pueden encontrar en un cierto rango.
Un ejemplo importante es el problema del círculo de Gauss. Este busca cuántos puntos con coordenadas enteras (como (1,2) o (3,0)) están dentro o sobre un círculo centrado en el origen con un radio r. Se sabe que la respuesta es aproximadamente el área del círculo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, \pi r^2 \, , más un término de error. La dificultad es encontrar límites precisos para este error.
Gauss demostró que el error es del orden de r. Sierpiński en 1906 mejoró esto, mostrando que el error es del orden de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): O(r^{2/3}) .
Métodos de la teoría analítica de números
Series de Dirichlet
Una herramienta muy poderosa en la teoría multiplicativa de números son las series de Dirichlet. Son funciones que se definen con una suma infinita:
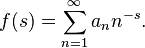
Estas series pueden ayudar a entender las funciones multiplicativas. Un método común es expresar una función multiplicativa como una serie de Dirichlet. Luego, se estudia esta serie como una función compleja y se usa esa información para entender la función original.
La función zeta de Riemann
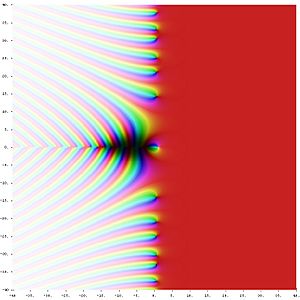
Euler descubrió una relación importante:
donde p es un número primo. Euler fue el primero en usar ideas del análisis para estudiar las propiedades de los números enteros. Esto marcó el inicio de la teoría analítica de números.
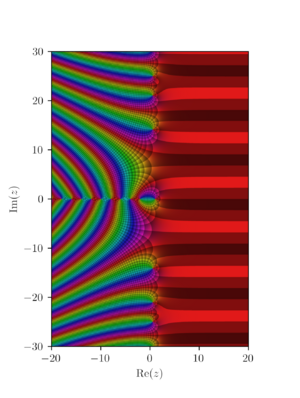
Riemann estudió esta función para valores complejos y la llamó función Zeta de Riemann, ζ(s). Hay mucha información sobre esta función.
Los matemáticos a menudo quieren saber qué tan preciso es el Teorema de los números primos. La fórmula de Riemann para π(x) muestra que el error en esta aproximación se puede expresar usando los ceros de la función zeta. En 1859, Riemann hizo una suposición muy famosa: que todos los ceros "no triviales" de ζ se encuentran en una línea específica. Esta suposición se conoce como la Hipótesis de Riemann. Tiene muchas implicaciones importantes en la teoría de números. Si la hipótesis fuera cierta, el error en el teorema de los números primos sería mucho menor.
Véase también
 En inglés: Analytic number theory Facts for Kids
En inglés: Analytic number theory Facts for Kids