Teoría de la información para niños

No debe confundirse con Ciencia de la información.

La comunicación es clave para entender la teoría de la información.

La teoría de la información, también conocida como teoría matemática de la comunicación, es una idea importante que crearon Claude E. Shannon y Warren Weaver a finales de los años 1940. Esta teoría estudia las reglas matemáticas que explican cómo se envía y se procesa la información. Se enfoca en cómo medir la información, cómo representarla y qué tan bien pueden los sistemas de comunicación transmitirla.

La teoría de la información es una parte de la teoría de la probabilidad. Investiga todo lo relacionado con la información, como los canales por donde viaja, cómo se comprime para que ocupe menos espacio y cómo se protege con la criptografía.

En pocas palabras, la "información" es un estado específico de algo físico. Es un estado que puede influir en su entorno o en otras cosas. Por lo tanto, la información es una característica que puede tener un sistema físico. Como es una característica de un sistema físico, sigue las leyes de la naturaleza, como el aumento de la entropía.

Historia de la Teoría de la Información

¿Cuándo surgió la teoría de la información?

La teoría de la información comenzó a desarrollarse a finales de los años cuarenta. Fue presentada por Claude E. Shannon en 1948, en un artículo llamado Una teoría matemática de la comunicación. En esa época, se buscaba mejorar la forma en que se usaban los canales de comunicación. La meta era enviar la mayor cantidad de información posible por un canal y medir su capacidad para lograr una transmisión de mensajes muy eficiente.

¿Quiénes fueron los pioneros de esta teoría?

Esta teoría es el resultado de trabajos que empezaron en los años 1910 con Andrei A. Markov. Después, en 1927, Ralph Hartley fue un precursor del lenguaje binario, que usa solo ceros y unos. En 1936, Alan Turing diseñó una máquina que podía procesar información usando símbolos.

Finalmente, Claude Elwood Shannon, un matemático e ingeniero electrónico, conocido como "el padre de la teoría de la información”, junto con Warren Weaver, ayudaron a completar y establecer la Teoría Matemática de la Comunicación en 1949. Weaver logró que la idea inicial fuera más amplia, creando un modelo sencillo: Fuente / codificador / mensaje / canal / decodificador / destino.

¿Por qué fue necesaria la teoría de la información?

La necesidad de una base teórica para la tecnología de la comunicación surgió porque los medios de comunicación como el teléfono, las redes de teletipo y los sistemas de radio se hicieron más complejos y se usaban masivamente. La teoría de la información también incluye otras formas de enviar y guardar información, como la televisión, los impulsos eléctricos en las computadoras y la grabación óptica de datos e imágenes.

El objetivo principal es asegurar que el envío de grandes cantidades de datos no pierda calidad, incluso si los datos se comprimen. Lo ideal es que los datos puedan recuperarse en su forma original al llegar a su destino.

Desarrollo del Modelo de Comunicación

¿Cómo funciona el modelo de Shannon?

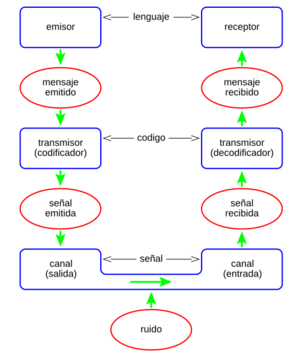
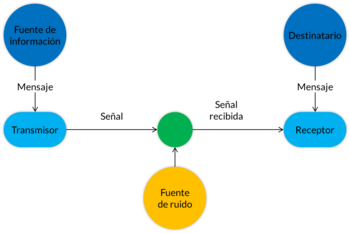
El modelo que propuso Shannon es un sistema general de comunicación. Comienza con una fuente de información que envía un mensaje. Un transmisor convierte este mensaje en una señal que viaja por un canal. En el canal, la señal puede ser afectada por algún ruido (interferencia). La señal sale del canal, llega a un receptor que la decodifica, convirtiéndola de nuevo en un mensaje que llega a un destinatario.

Con este modelo, se busca encontrar la forma más económica, rápida y segura de codificar un mensaje, para que el ruido no complique su transmisión. Para que esto funcione, el destinatario debe entender la señal correctamente. Aunque se use el mismo código, no siempre significa que el destinatario captará el significado exacto que el emisor quiso dar al mensaje.

La codificación puede ser la transformación de voz o imágenes en señales eléctricas, o el cifrado de mensajes para proteger su privacidad. Un concepto clave en esta teoría es que la cantidad de información en un mensaje es un valor matemático que se puede medir. La "cantidad" no se refiere al tamaño de los datos, sino a la probabilidad de que un mensaje, de entre varios posibles, sea recibido. Cuanto menos probable sea un mensaje, más información se considera que contiene. Si se sabe con seguridad que un mensaje será recibido, su cantidad de información es cero.

Propósito de la Teoría de la Información

¿Qué busca la teoría de la información?

Otro aspecto importante de esta teoría es la capacidad de resistir la distorsión causada por el ruido, la facilidad para codificar y decodificar, y la velocidad de transmisión. Por eso se dice que un mensaje puede tener muchos significados, y el destinatario elige el que debe darle, siempre que compartan el mismo código.

La teoría de la información tiene algunas limitaciones. Por ejemplo, el significado que se quiere transmitir no es tan importante como el número de opciones necesarias para definir un hecho sin ambigüedad. Si un mensaje se elige entre solo dos opciones diferentes, la teoría de Shannon dice que el valor de la información es uno. Esta unidad de información se llama bit. Para que el valor de la información sea un bit, todas las opciones deben ser igual de probables y estar disponibles.

Es importante saber si la fuente de información puede elegir cualquier opción con la misma libertad o si hay algo que la influya a elegir una en particular. La cantidad de información aumenta cuando todas las opciones son igual de probables o cuando hay más opciones. Sin embargo, en la comunicación real, no todas las opciones son igual de probables. Esto se conoce como un proceso estocástico de Márkov. Un tipo de Márkov dice que una secuencia de símbolos está organizada de tal manera que cualquier parte de esa secuencia es representativa de toda la cadena completa.

Aplicaciones de la Teoría en la Tecnología

¿Cómo se relaciona la teoría con Internet?

La Teoría de la Información sigue siendo muy importante hoy en día, especialmente con Internet. Desde el punto de vista social, Internet ofrece muchos beneficios, dando a las personas oportunidades únicas para acceder a una gran cantidad de información digital.

Internet se originó de un proyecto del departamento de defensa de los Estados Unidos llamado ARPANET (Advanced Research Projects Agency Network), que comenzó en 1969. Su objetivo principal era investigar y desarrollar protocolos de comunicación para redes grandes que pudieran conectar diferentes tipos de redes y seguir funcionando incluso si una parte de la red fallaba.

Estas investigaciones llevaron al protocolo TCP/IP (Transmission Control Protocol/Internet Protocol), un sistema de comunicaciones muy fuerte y confiable que integra todas las redes que forman Internet. El gran crecimiento de Internet se debe en parte a que es una red que recibe fondos de los gobiernos de los países que la usan, lo que hace que el servicio sea casi gratuito. A principios de 1994, muchas empresas comerciales empezaron a usar Internet, lo que marcó una nueva etapa en su desarrollo.

¿Cómo funciona TCP/IP?

En términos generales, TCP/IP toma la información que quieres enviar, la divide en "paquetes" y la vuelve a unir cuando se recibe. Estos paquetes son como sobres de correo: TCP/IP guarda la información, cierra el sobre y le pone la dirección de destino y la dirección de quien la envía. Así, los paquetes viajan por la red hasta que llegan a su destino. Una vez allí, la computadora de destino "abre" el sobre y procesa la información. Si es necesario, envía una respuesta a la computadora de origen usando el mismo proceso.

Cada máquina conectada a Internet tiene una dirección única, lo que asegura que la información llegue al lugar correcto. Hay dos formas de dar direcciones: con letras o con números. Las computadoras usan las direcciones numéricas para enviar paquetes de información, pero las direcciones con letras se crearon para que los humanos las recordaran más fácilmente. Una dirección numérica tiene cuatro partes, separadas por puntos.

Ejemplo:   sedet.com.mx  107.248.185.1

¿Qué otros usos tiene la teoría de la información?

Una de las aplicaciones de la teoría de la información son los archivos ZIP. Estos son documentos que se comprimen para enviarlos por correo electrónico o para guardarlos. Comprimir los datos permite que la transmisión se complete en menos tiempo. En el lugar de destino, un programa se usa para "descomprimir" el archivo, restaurando los documentos a su forma original.

La teoría de la información también se usa con otros tipos de archivos. Por ejemplo, los archivos de audio y video que escuchas en un reproductor de MP3 o MP4 se comprimen para que sea fácil descargarlos y guardarlos en el dispositivo. Cuando accedes a ellos, se descomprimen para que puedas usarlos de inmediato.

Componentes Clave de la Teoría

Esquema de la comunicación ideado por Claude E. Shannon.

Fuente de Información

Una fuente es cualquier cosa que produce mensajes. Por ejemplo, una computadora puede ser una fuente y sus archivos, los mensajes. Un dispositivo que envía datos puede ser una fuente y los datos enviados, los mensajes. Una fuente es un conjunto de todos los mensajes posibles que puede emitir. En la compresión de datos, la fuente sería el archivo a comprimir y los mensajes, los caracteres que forman ese archivo.

Tipos de Fuentes

Según cómo generan sus mensajes, una fuente puede ser aleatoria o determinista. Según la relación entre los mensajes que emite, una fuente puede ser estructurada o no estructurada (o caótica).

Para la teoría de la información, son interesantes las fuentes aleatorias y estructuradas. Una fuente es aleatoria cuando no se puede predecir cuál será el siguiente mensaje que emitirá. Una fuente es estructurada cuando tiene cierta repetición o patrón (redundancia). Una fuente no estructurada o de información pura es aquella donde todos los mensajes son completamente aleatorios, sin ninguna relación o sentido aparente. Este tipo de fuente emite mensajes que no se pueden comprimir. Para que un mensaje pueda comprimirse, debe tener cierto grado de repetición; la información pura no se puede comprimir sin perder parte de su contenido.

Mensaje

Un mensaje es un conjunto de ceros y unos. Un archivo, un paquete de datos que viaja por una red o cualquier cosa que tenga una representación binaria (en ceros y unos) puede considerarse un mensaje. El concepto de mensaje también se aplica a alfabetos con más de dos símbolos, pero como hablamos de información digital, casi siempre nos referiremos a mensajes binarios.

Código

Un código es un conjunto de unos y ceros que se usan para representar un mensaje, siguiendo reglas o acuerdos previos. Por ejemplo, el mensaje 0010 se puede representar con el código 1101 si se usa para codificar la función de negación (NOT) en lógica binaria. La forma en que codificamos es una elección. A veces, un mensaje se puede representar con un código más corto que el mensaje original.

Si un mensaje S se codifica usando un algoritmo de tal manera que cada S se convierte en L(S) bits, entonces la información contenida en el mensaje S se define como la cantidad mínima de bits necesarios para codificarlo.

Información

La información que contiene un mensaje es proporcional a la cantidad mínima de bits que se necesitan para representarlo. Para entender mejor el concepto de información, veamos un ejemplo. Imagina que estás leyendo un mensaje y has leído "cadena de c". Es muy probable que el mensaje continúe con "caracteres". Si efectivamente recibes "caracteres" a continuación, la cantidad de información que te llegó es muy baja, porque ya podías predecirlo. Los mensajes que son muy probables de aparecer aportan menos información que los mensajes menos probables. Si después de "cadena de c" lees "himichurri", la cantidad de información que recibes es mucho mayor, porque era algo inesperado.

Entropía e Información

La información se trata como una cantidad física, y la información de una secuencia de símbolos se describe usando la entropía. Esto se basa en la idea de que los canales de comunicación no son perfectos. La entropía ayuda a estudiar diferentes formas de enviar información y la cantidad de información útil que se puede transmitir por un canal.

La información necesaria para describir un sistema físico está relacionada con su entropía. En algunas áreas de la física, obtener información del estado actual de un sistema requiere reducir su entropía. La entropía del sistema (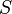 $S$ ) y la cantidad de información ( 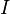$I$ ) que se puede extraer están relacionadas así:

$S \ge S - I \ge 0$

Entropía de una Fuente

Artículo principal: Entropía (información)

Según la teoría de la información, el nivel de información de una fuente se puede medir con su entropía. Los estudios sobre la entropía son muy importantes en esta teoría y se deben principalmente a C. E. Shannon. También hay muchas propiedades de la entropía de variables aleatorias gracias a A. Kolmogorov.

Cuando una fuente F emite mensajes, es común que los mensajes no tengan la misma probabilidad de aparecer, sino que algunos sean más probables que otros. Para codificar los mensajes de una fuente, intentaremos usar menos bits para los mensajes más probables y más bits para los menos probables. Así, el promedio de bits usados para codificar los mensajes será menor que el promedio de bits de los mensajes originales. Esta es la base de la compresión de datos.

A este tipo de fuente se le llama fuente de orden-0, porque la probabilidad de que aparezca un mensaje no depende de los mensajes anteriores. Las fuentes de orden superior se pueden representar como una fuente de orden-0 usando técnicas de modelado adecuadas.

Definimos la probabilidad de que un mensaje aparezca en una fuente como el número de veces que aparece ese mensaje dividido por el total de mensajes. Si P_i es la probabilidad de que aparezca el mensaje-i de una fuente, y L_i es la longitud del código usado para representar ese mensaje, la longitud promedio de todos los mensajes codificados de la fuente se puede calcular como:

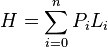
$H=\sum_{i=0}^n P_i L_i$

Este promedio ponderado de las longitudes de los códigos, según sus probabilidades de aparición, se llama "Entropía de la fuente" (H) y es muy importante. La entropía de la fuente nos dice el nivel máximo de compresión que podemos lograr para un conjunto de datos. Si consideramos un archivo como fuente y calculamos las probabilidades de aparición de cada carácter en él, podemos estimar la longitud promedio del archivo comprimido. Se ha demostrado que no es posible comprimir un mensaje o archivo estadísticamente más allá de su entropía. Esto significa que, considerando solo la frecuencia de aparición de cada carácter, la entropía de la fuente nos da el límite teórico de compresión. Con otras técnicas no estadísticas, quizás se pueda superar este límite.
El objetivo de la compresión de datos es encontrar los valores de L_i que hagan que H sea lo más pequeño posible. Además, los L_i deben depender de los P_i, ya que queremos que los códigos de los caracteres más frecuentes sean más cortos. Así, se plantea:

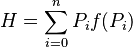
$H=\sum_{i=0}^n P_i f(P_i)$

Después de complejos cálculos matemáticos que Shannon demostró, se llega a que H es mínimo cuando f(P_i) = log₂ (1/P_i). Entonces:

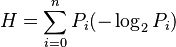
$H=\sum_{i=0}^n P_i (-\log_2 P_i)$

La longitud mínima con la que se puede codificar un mensaje se calcula como L_i=log₂(1/P_i) = -log₂(P_i). Esto nos da una idea de la longitud que deben tener los códigos para los caracteres de un archivo, según su probabilidad de aparición. Reemplazando L_i, podemos escribir H como:

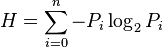
$H=\sum_{i=0}^n -P_i \log_2 P_i$

De esto se deduce que la entropía de la fuente solo depende de la probabilidad de aparición de cada mensaje. Por eso son tan importantes los compresores estadísticos, que se basan en la probabilidad de aparición de cada carácter. Shannon demostró que no es posible comprimir una fuente estadísticamente más allá del nivel que indica su entropía.

Otros Conceptos de la Teoría

Fuentes de información
- Entropía
- Información mutua
- Neguentropía
- Teorema de muestreo de Nyquist-Shannon

Canales
- Capacidad

Compresión de datos
- Codificación de fuente
- Códigos no-singulares
- Códigos unívocamente decodificables
  - Extensión de código
- Códigos prefijo (o códigos instantáneos)

Control de errores
- ARQ
- FEC
  - Parada y espera
  - Rechazo múltiple
  - Rechazo selectivo
- Técnicas híbridas
  - Concatenación de códigos
  - Tipo 1
  - Tipo 2

Detección de errores
- Bits de redundancia
  - Métodos de control de errores
    - Paridad

* Códigos autochequeo y autocorrectores ** Códigos de bloque *** Distancia Hamming ** Paridad horizontal y vertical

- - - Códigos lineales

* Códigos cíclicos ** CRC16 ** CRC32

Véase también

En inglés: Information theory Facts for Kids

Información de Fisher
Paradoja de Freedman
Sistema complejo
Teoría algorítmica de la información
Teoría de la información integrada

Obtenido de «https://ninos.kiddle.co/index.php?title=Teoría_de_la_información&oldid=5004675»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Teoría de la información para Niños. Enciclopedia Kiddle.