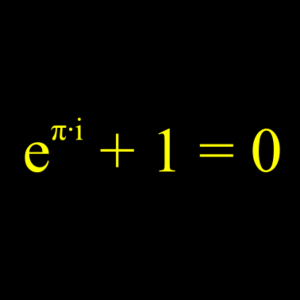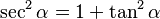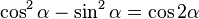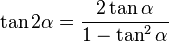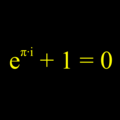robot de la enciclopedia para niños

Identidad (matemática) para niños

Enciclopedia para niños
No debe confundirse con igualdad matemática, Identidad o elemento identidad.
Archivo:VignetteEulerIdentity
La Identidad de Euler

En matemáticas, una identidad es como una regla especial que nos dice que dos expresiones matemáticas, aunque se vean diferentes, ¡son en realidad lo mismo! Imagina que tienes dos caminos para llegar al mismo lugar; una identidad es la confirmación de que ambos caminos te llevan exactamente al mismo destino.

Lo más importante de una identidad es que es una igualdad que siempre es verdad, sin importar qué números pongas en las letras (variables) que aparecen en ella. Por eso, las identidades son muy útiles para cambiar una expresión matemática por otra que es igual, pero que quizás nos ayude a resolver un problema más fácilmente.

¿Qué es una identidad matemática?

Una identidad matemática es una afirmación de que dos expresiones son iguales para todos los valores posibles de las variables que contienen. Es como una verdad universal en el mundo de los números.

Ejemplos sencillos de identidades

Para entenderlo mejor, veamos algunos ejemplos:

  • Sumar cero: Si tienes un número a y le sumas 0, el resultado siempre será a.

* a + 0 = a Esta es una identidad porque siempre se cumple, no importa qué número sea a.

  • La Identidad de Euler: Esta es una de las identidades más famosas y conecta varios números especiales de las matemáticas:

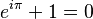* e^{i \pi} + 1 = 0\; Aquí, 'e', 'i', 'π' y los números 0 y 1 son constantes matemáticas, es decir, números que tienen un valor fijo. Esta identidad es sorprendente porque une estos números de una forma muy elegante. La Identidad de Euler es un caso especial de una regla más grande llamada la fórmula de Euler.

Identidades en trigonometría

La trigonometría es la parte de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos. En ella, hay muchas identidades que nos ayudan a hacer cálculos.

  • Identidad fundamental: Una de las más conocidas es:

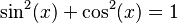* \sin^2(x) + \cos^2(x) = 1 Esta identidad es siempre cierta para cualquier número x. Las funciones seno (sin) y coseno (cos) son muy importantes en trigonometría.

Identidades notables en álgebra

Algunas identidades en álgebra son tan importantes que se les llama "notables". Nos ayudan a hacer cálculos más rápido o a descomponer expresiones en partes más sencillas.

  • El cuadrado de una suma: Una identidad muy útil es:

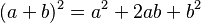* (a + b)^2 = a^2 +2ab + b^2 Esto significa que si sumas dos números (a y b) y luego elevas el resultado al cuadrado, es lo mismo que elevar cada número al cuadrado y luego sumar el doble de su producto. Esta identidad es siempre cierta para cualquier par de números a y b.

Identidades aritméticas importantes

Las identidades aritméticas nos ayudan a entender patrones en los números.

  • Suma de los primeros números naturales: Si quieres sumar todos los números desde el 1 hasta un número n, hay una identidad que te da el resultado rápidamente:

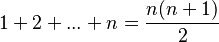* 1 + 2 + ... + n = \frac{n(n+1)}{2} Por ejemplo, si quieres sumar 1+2+3+4+5, puedes usar la fórmula: (5 * (5+1)) / 2 = (5 * 6) / 2 = 30 / 2 = 15. ¡Es mucho más rápido!

  • Suma de cubos consecutivos: Otra identidad interesante es que la suma de los cubos de tres números naturales seguidos siempre es un múltiplo de 9.

* n^3 + (n+1)^3 + (n+2)^3 = 9k \, Aquí, k es un número entero.

Identidades algebraicas clave

Estas identidades nos permiten manipular expresiones algebraicas.

  • Diferencia de cuadrados: La diferencia de los cuadrados de dos números es igual al producto de la suma de esos números por su diferencia.

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^2 - b^2 = (a - b)(a + b)

  • Factorización de la diferencia de cubos: Esta identidad nos permite descomponer la resta de dos números elevados al cubo.

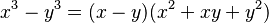
* x^3 -y^3 = (x -y)(x^2 + xy + y^2)

Identidades trigonométricas adicionales

Además de la identidad fundamental, hay otras identidades importantes en trigonometría:

  • \sec^2 \alpha = 1+ \tan^2 \alpha
  • \cos^2 \alpha -\sin^2 \alpha = \cos 2 \alpha
  • \tan 2 \alpha = \frac{2\tan \alpha}{1- \tan^2 \alpha}

Identidades logarítmicas

Los logaritmos son una forma de encontrar el exponente al que hay que elevar un número base para obtener otro número. Las identidades logarítmicas nos ayudan a trabajar con ellos. Recuerda que la base del logaritmo debe ser un número positivo diferente de 1.

  • Logaritmo de un producto: El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

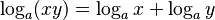
* \log_a (xy) = \log_a x +\log_a y

  • Cambio de base: Esta identidad nos permite cambiar la base de un logaritmo a otra base que nos sea más conveniente.

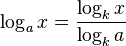
* \log_a x = \frac{\log_k x}{\log_k a}

Galería de imágenes

  • VignetteEulerIdentity

    La Identidad de Euler

Véase también

Kids robot.svg En inglés: Identity (mathematics) Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Identidad_(matemática)&oldid=4711660»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Identidad (matemática) para Niños. Enciclopedia Kiddle.