Poliedro conjugado para niños
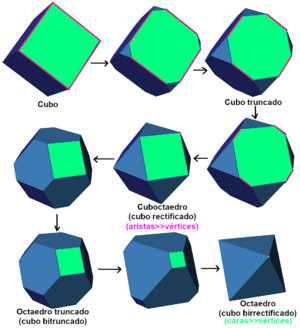
El dual de un poliedro es como su "compañero" o "reflejo". Imagina que tienes un poliedro, como un cubo. Su dual es otro poliedro donde las esquinas (vértices) del dual corresponden a las caras del cubo original. Y las caras del dual corresponden a las esquinas del cubo original.
Por ejemplo, el dual de un cubo es un octaedro, y el dual de un octaedro es un cubo. Si tomas el dual de un poliedro y luego vuelves a tomar el dual de ese resultado, obtendrás una figura muy parecida al poliedro original.
Contenido
¿Cómo se relacionan los poliedros duales?
Hay varias maneras de entender la relación entre un poliedro y su dual. Las más importantes para los poliedros regulares son:
- La reciprocidad polar
- La dualidad topológica
Reciprocidad polar: el espejo matemático
La dualidad de los poliedros se explica a menudo usando algo llamado "reciprocidad polar" con respecto a una esfera imaginaria que está justo en el centro del poliedro. Piensa en esta esfera como un espejo especial.
Funciona así: cada esquina (vértice) del poliedro original se conecta con una cara del poliedro dual. La línea que va desde el centro de la esfera hasta la esquina del poliedro original es perpendicular al plano de la cara del poliedro dual. Es como si cada esquina del original "apuntara" directamente al centro de una cara del dual.
De esta forma, las esquinas del poliedro dual son como los "reflejos" de las caras del poliedro original. Y las caras del dual son los "reflejos" de las esquinas del original. Si dos esquinas del poliedro original están unidas por una arista, entonces las dos caras correspondientes del poliedro dual se encontrarán para formar una arista del dual.
Este concepto se puede aplicar a figuras en más dimensiones, llamadas politopos. Un politopo es una forma geométrica con "caras" en varias dimensiones.
Duales especiales: los canónicos
La forma exacta de un poliedro dual puede variar un poco dependiendo de cómo se use la esfera imaginaria para la reciprocidad. Sin embargo, si un poliedro tiene varios ejes de simetría (líneas imaginarias por las que puedes doblarlo y que se vea igual), estos ejes se cruzarán en un punto central. Este punto se usa generalmente como el centro de la esfera.
Existe una forma especial de poliedro, llamada "forma canónica", donde todas sus aristas tocan una esfera central de una manera muy equilibrada. Si un poliedro está en su forma canónica y se le aplica la reciprocidad polar con respecto a esa esfera, su dual también estará en su forma canónica. A estos se les llama "pares duales canónicos".
Dualidad topológica: la forma importa, no el tamaño
A veces, un poliedro dual puede ser "estirado" o "aplastado" de tal manera que ya no se puede obtener por reciprocidad polar. Aun así, decimos que los dos poliedros son "topológicamente duales". Esto significa que tienen la misma estructura de conexiones entre sus vértices, aristas y caras, aunque sus formas geométricas no sean idénticas.
Imagina que tienes un poliedro hecho de alambre y goma elástica. Puedes estirarlo o encogerlo, y seguirá siendo el mismo poliedro topológicamente, aunque su forma cambie. Lo mismo ocurre con los duales topológicos.
Un politopo abstracto es una forma de describir un poliedro solo por cómo sus partes (vértices, aristas, caras) están conectadas entre sí, sin importar su tamaño o forma exacta. El dual de un poliedro abstracto se obtiene simplemente "invirtiendo" esas conexiones.
Construcción de Dorman Luke
Para algunos poliedros especiales, llamados "uniformes", existe un método llamado "construcción de Dorman Luke" que ayuda a encontrar las caras de su poliedro dual.
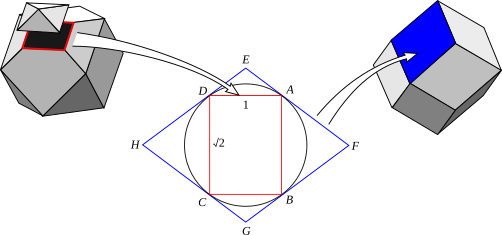
Por ejemplo, si tienes un cuboctaedro, puedes usar este método para encontrar una cara de su dual, el rombododecaedro.
Los pasos son:
- Dibuja una sección especial del poliedro original, llamada "figura de vértice".
- Dibuja un círculo que toque todas las esquinas de esa figura de vértice.
- Dibuja líneas que sean tangentes (que toquen en un solo punto) a ese círculo en cada esquina.
- Los puntos donde estas líneas tangentes se cruzan formarán una nueva figura.
- Esa nueva figura es una cara del poliedro dual.
Este método funciona si el poliedro tiene una esfera central que toca todas sus aristas y si su figura de vértice es un polígono que se puede inscribir en un círculo.
Poliedros auto-duales
Un poliedro es "auto-dual" si su dual es exactamente igual a él mismo.
- Topológicamente auto-dual: Significa que la forma en que sus vértices, aristas y caras están conectados es la misma que la de su dual.
- Geométricamente auto-dual: Además de ser topológicamente auto-dual, su forma es idéntica a la de su dual, quizás solo girada o reflejada.
El ejemplo más famoso de un poliedro auto-dual es el tetraedro regular (una pirámide de base triangular con todas las caras iguales). Si tomas el dual de un tetraedro regular, obtendrás otro tetraedro regular.
Hay muchísimos poliedros auto-duales. Algunas familias comunes son las pirámides y las pirámides elongadas.
 base 3 |
 base 4 |
 base 5 |
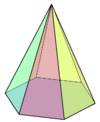 base 6 |
 base 3 |
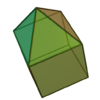 base 4 |
base 5 |
 base 3 |
 base 4 |
 base 5 |
 base 6 |
 base 7 |
Poliedros compuestos auto-duales
Si combinas un poliedro con su propio dual, el resultado es una figura auto-dual. Un ejemplo famoso es la estrella octángula, que se forma al combinar dos tetraedros.
Politopos y teselados duales
La idea de dualidad no es solo para poliedros. Se puede aplicar a formas en cualquier número de dimensiones, llamadas politopos. En dos dimensiones, por ejemplo, hablamos de polígonos duales.
Politopos y teselados auto-duales
Algunos politopos y teselados (patrones que cubren una superficie sin huecos ni superposiciones) también son auto-duales.

Los politopos regulares auto-duales incluyen:
- Todos los polígonos regulares (como un cuadrado o un triángulo equilátero).
- El tetraedro regular.
- El icositetracoron (una figura de 24 celdas en cuatro dimensiones).
- En general, todos los símplex regulares (las formas más simples en cada dimensión).
Los teselados regulares auto-duales en el espacio euclidiano (nuestro espacio normal) son:
- El apeirógono (un polígono con infinitos lados).
- El teselado cuadrado (como un tablero de ajedrez).
- El panal cúbico (como una pared de ladrillos).
Véase también
 En inglés: Dual polyhedron Facts for Kids
En inglés: Dual polyhedron Facts for Kids
- Poliedro autodual
- Geometría proyectiva
- Grafo dual
- Plano proyectivo
- Dualidad
- Recta polar
- Sólidos arquimedianos
- Sólidos de Catalan
- Sólidos de Johnson
- Sólidos de Kepler-Poinsot
- Sólidos platónicos