Fracción para niños

Enciclopedia para niños

En matemáticas, una fracción es una forma de representar una parte de un todo. Imagina que tienes una pizza y la divides en varias porciones iguales. Una fracción te dice cuántas de esas porciones tienes.

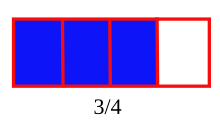
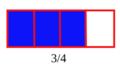
Una fracción se escribe con dos números separados por una línea. El número de arriba se llama numerador y te dice cuántas partes tienes. El número de abajo se llama denominador y te indica en cuántas partes iguales se dividió el todo. Por ejemplo, en la fracción $\tfrac{3}{4}$ , el 3 es el numerador y el 4 es el denominador. Esto significa que tienes 3 partes de un total de 4.

Las fracciones son parte de un grupo de números llamados números racionales. Estos son todos los números que se pueden escribir como una fracción, donde el denominador no es cero.

tres cuartos más un cuarto suman un todo.

Contenido

¿Cómo representamos las fracciones?
- Dibujos y ejemplos
Tipos de fracciones
Operaciones con fracciones
Historia de las fracciones
Galería de imágenes
Véase también

¿Cómo representamos las fracciones?

Dibujos y ejemplos

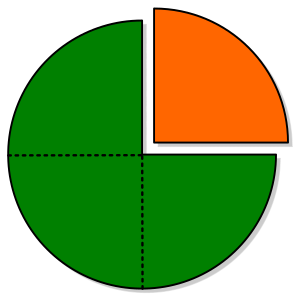
Podemos usar dibujos para entender mejor las fracciones. Si dibujamos una figura, como un círculo o un cuadrado, y la dividimos en partes iguales, podemos colorear algunas de esas partes para mostrar una fracción.

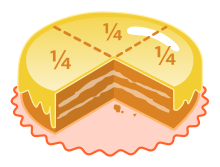
Si quitamos 1/4 de un pastel, quedan 3/4.

Por ejemplo, si un pastel se divide en 4 partes iguales y te comes 1, te quedan 3 de esas 4 partes, lo que se representa como $\tfrac{3}{4}$ .

Cuando leemos una fracción, el denominador se lee de una forma especial. Por ejemplo:

* $\tfrac{1}{2}$ se lee "un medio". * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{1}{3} se lee "un tercio". * $\tfrac{1}{4}$ se lee "un cuarto". * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{3}{5} se lee "tres quintos". * Para denominadores mayores de 10, se añade la terminación "avos" (ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{1}{11} se lee "un onceavo").

Tipos de fracciones

Existen diferentes tipos de fracciones, cada una con sus propias características:

Fracción simple o común

Una fracción simple es la forma más básica de una fracción, como $\tfrac{3}{4}$ . El numerador y el denominador son números enteros y el denominador no es cero.

Fracción propia e impropia

Una fracción propia es aquella en la que el numerador es más pequeño que el denominador. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{1}{3} o $\tfrac{3}{4}$ . Su valor es menor que 1.
Una fracción impropia es aquella en la que el numerador es igual o más grande que el denominador. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{5}{2} o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{7}{7} . Su valor es igual o mayor que 1.

Fracción mixta

Una fracción mixta combina un número entero con una fracción propia. Es una forma de escribir fracciones impropias. Por ejemplo, la fracción impropia Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{5}{2} se puede escribir como la fracción mixta Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2\tfrac{1}{2} (dos y un medio). Esto significa 2 unidades completas y media unidad más.

Fracción inversa

La fracción inversa de una fracción se obtiene al cambiar de lugar el numerador y el denominador. Por ejemplo, la fracción inversa de $\tfrac{2}{3}$ es $\tfrac{3}{2}$ .

Fracción decimal y porcentaje

Una fracción decimal es una fracción cuyo denominador es una potencia de 10 (como 10, 100, 1000, etc.). Estas fracciones se pueden escribir fácilmente como números decimales. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{8}{10} se escribe como 0.8, y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{83}{100} como 0.83.

Un porcentaje es una forma especial de fracción decimal donde el denominador siempre es 100. Se usa el signo % para indicarlo. Por ejemplo, $\tfrac{3}{4}$ es lo mismo que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{75}{100} , que se expresa como 75%.

Operaciones con fracciones

Fracciones equivalentes

Dos fracciones son equivalentes si representan la misma cantidad, aunque se escriban con números diferentes. Por ejemplo, $\tfrac{1}{2}$ y $\tfrac{2}{4}$ son fracciones equivalentes, porque ambas representan la mitad de algo.

Para saber si dos fracciones son equivalentes, puedes multiplicar el numerador de la primera por el denominador de la segunda, y el denominador de la primera por el numerador de la segunda. Si los resultados son iguales, las fracciones son equivalentes. Por ejemplo, para $\tfrac{1}{2}$ y $\tfrac{2}{4}$ :

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 \times 4 = 4
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 \times 2 = 4

Como ambos resultados son 4, las fracciones son equivalentes.

Comparación de fracciones

Comparar fracciones significa saber cuál es mayor o menor.

Si tienen el mismo denominador: La fracción con el numerador más grande es la mayor. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{5}{7} es mayor que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{2}{7} porque 5 es mayor que 2.
Si tienen el mismo numerador: La fracción con el denominador más pequeño es la mayor. Por ejemplo, $\tfrac{2}{3}$ es mayor que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{2}{5} . Imagina que tienes dos pasteles iguales y uno lo divides entre 3 personas y el otro entre 5. Las porciones del pastel dividido entre 3 serán más grandes.
Si tienen diferentes numeradores y denominadores: Puedes encontrar un denominador común para ambas fracciones. Una forma sencilla es multiplicar el numerador y el denominador de cada fracción por el denominador de la otra. Por ejemplo, para comparar $\tfrac{2}{3}$ y $\tfrac{1}{2}$ :

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{2}{3} = \tfrac{2 \times 2}{3 \times 2} = \tfrac{4}{6} * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{1}{2} = \tfrac{1 \times 3}{2 \times 3} = \tfrac{3}{6} Ahora que tienen el mismo denominador (6), podemos ver que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{4}{6} es mayor que $\tfrac{3}{6}$ , así que $\tfrac{2}{3}$ es mayor que $\tfrac{1}{2}$ .

Suma y resta de fracciones

Si tienen el mismo denominador: Suma o resta los numeradores y mantén el mismo denominador.

* Ejemplo de suma: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{2}{7} + \tfrac{3}{7} = \tfrac{5}{7} * Ejemplo de resta: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{7}{12} - \tfrac{1}{12} = \tfrac{6}{12} (que se puede simplificar a $\tfrac{1}{2}$ )

Si tienen distinto denominador: Primero, encuentra un denominador común (el mínimo común múltiplo de los denominadores es el más eficiente). Luego, convierte cada fracción a una fracción equivalente con ese denominador común y, finalmente, suma o resta los numeradores.

* Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{2}{7} + \tfrac{1}{3} * El mínimo común múltiplo de 7 y 3 es 21. * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{2}{7} = \tfrac{2 \times 3}{7 \times 3} = \tfrac{6}{21} * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{1}{3} = \tfrac{1 \times 7}{3 \times 7} = \tfrac{7}{21} * Ahora suma: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{6}{21} + \tfrac{7}{21} = \tfrac{13}{21}

Multiplicación y división de fracciones

Multiplicación: Multiplica los numeradores entre sí y los denominadores entre sí.

* Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{3}{4} \times \tfrac{5}{2} = \tfrac{3 \times 5}{4 \times 2} = \tfrac{15}{8}

División: Multiplica la primera fracción por la fracción inversa de la segunda. Esto es como "multiplicar en cruz".

* Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{2}{3} \div \tfrac{1}{4} * Invierte la segunda fracción ( $\tfrac{1}{4}$ se convierte en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{4}{1} ). * Ahora multiplica: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{2}{3} \times \tfrac{4}{1} = \tfrac{2 \times 4}{3 \times 1} = \tfrac{8}{3}

Historia de las fracciones

Las fracciones se han usado desde hace mucho tiempo.

En el Antiguo Egipto, se usaban fracciones especiales llamadas "fracciones egipcias", que eran sumas de fracciones con numerador 1 (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{1}{2} + \tfrac{1}{3} ). Usaban un jeroglífico de una boca abierta para representar la barra de fracción.
Los babilonios usaban fracciones con denominadores basados en el número 60.
Los matemáticos chinos también usaban fracciones y un sistema de varillas para representarlas.
En la Edad Media, se empezó a usar la línea horizontal para separar el numerador del denominador, lo que dio origen a las fracciones que conocemos hoy.
Las fracciones decimales, que tienen denominadores como 10, 100, etc., se cree que fueron conocidas por los matemáticos chinos en el siglo I.
Leonardo de Pisa (conocido como Fibonacci) ayudó a difundir el uso de las fracciones en Europa en el siglo XIII con su libro Liber Abaci.
El uso moderno de las fracciones decimales se hizo popular gracias a Simon Stevin en el siglo XVI.

Las fracciones son una herramienta muy importante en matemáticas y nos ayudan a entender y trabajar con partes de un todo en nuestra vida diaria.

Galería de imágenes

Véase también

En inglés: Fractions Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Fracción&oldid=4757397»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Fracción para Niños. Enciclopedia Kiddle.