Isodecágono para Niños

Datos para niños Isodecágono
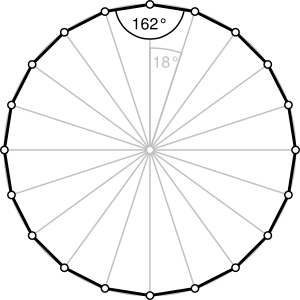
Un isodecágono regular
Características
Tipo	Polígono regular
Lados	20
Vértices	20
Grupo de simetría	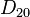$D_{20}$ , orden 2x20
Símbolo de Schläfli	{20}, t{10} (isodecágono regular)
Diagrama de Coxeter-Dynkin
Polígono dual	Autodual
Área	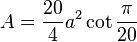$A = \frac{20}{4}a^2 \cot \frac{\pi}{20}$ (lado $a$ )
Ángulo interior	162°
Propiedades
Convexo, isogonal, cíclico

En geometría, un isodecágono o icoságono es un polígono de 20 lados y 20 vértices. El isodecágono es un polígono construible, mediante la bisección de los lados de un decágono regular.

Propiedades

Un isodecágono o icoságono tiene 170 diagonales, que se puede obtener aplicando la fórmula general para determinar el número de diagonales de un polígono, $D=\tfrac{n(n-3)}{2}$ ; siendo el número de lados $n=20$ , tenemos:

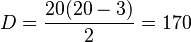
D=\frac{20(20-3)}{2}=170

La suma de todos los ángulos internos de cualquier isodecágono es 3240 grados o $18\pi$ radianes.

Isodecágono regular

Un isodecágono regular y sus ángulos principales

Un isodecágono regular es el que tiene todos sus lados de la misma longitud y todos sus ángulos internos iguales. Cada ángulo interno del isodecágono regular mide 162 grados o $9\pi/10$ radianes. Cada ángulo externo del isodecágono regular mide 18º o $\pi/10$ rad.

Para obtener el perímetro P de un isodecágono regular, multiplíquese la longitud de uno de sus lados t por veinte (el número de lados n del polígono).

P = n\cdot t = 20\ t

El área A de un isodecágono regular se puede calcular a partir de la longitud t de uno de sus lados, de la siguiente forma:

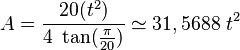A = \frac{20(t^2)}{4\ \tan(\frac{\pi}{20})}\simeq 31,5688\ t^2

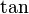donde $\pi$ es la constante pi y $\tan$ es la función tangente calculada en radianes.

Si se conoce la longitud de la apotema a del polígono, otra alternativa para calcular el área es:

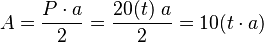
A = \frac{P\cdot a}{2} = \frac{20(t)\ a}{2} = 10(t \cdot a)

Utilización

La gran rueda del popular programa de juegos estadounidense "The Price Is Right" tiene una sección transversal isodecagonal.

Se descubrió que The Globe, el teatro al aire libre utilizado por la compañía de actores de William Shakespeare, fue construido sobre una base icosagonal cuando se realizó una excavación parcial en 1989.

Como ruta golígonoal, esvástica se considera un isodecágono irregular.

Un cuadrado, un pentágono y un isodecágono regulares pueden formar un teselado regular que recubre el plano por completo.

Construcción

Como $20 = 2 2 \times5$ , el isodecágono regular es construible usando regla y compás, o procediendo a la bisección de los lados de un decágono regular, o a la doble bisección de los lados de un pentágono regular:

Construcción de un isodecágono regular	Otra construcción de un isodecágono regular

La proporción áurea en un isodecágono

En la construcción con longitud de lado dada, el arco circular alrededor de $C$ con radio $CD$ , comparte con el segmento $E 20 F$ la relación de la proporción áurea.

\frac{\overline{ E_{20}E_1}}{\overline{E_1 F}} = \frac{\overline{E_{20} F}}{\overline{ E_{20}E_1}} = \frac{1+ \sqrt{5}}{2} =\varphi \approx 1.618

Isodecágono con longitud de lado dada, animación (la construcción es muy similar a la del decágono con longitud de lado dada)

Simetría

Simetrías de un isodecágono regular. Los ejes de simetría azules atraviesan vértices, los violetas pasan por el centro de los lados y el orden de las simetrías de rotación se anota en el centro. Los vértices están coloreados según su posición de simetría

El isodecágono regular posee simetría diedral $Dih 20$ de orden 40. Incluye 5 subgrupos de simetría diedrales: $(Dih 10, Dih 5)$ y $(Dih 4, Dih 2, y Dih 1)$ , y 6 simetrías cíclicas: $(Z 20, Z 10, Z 5)$ y ( $Z 4, Z 2, Z 1)$ . Estas 10 simetrías dan origen a 16 tipos de formas distintas de isodecágono, un número mayor de formas que de simetrías porque los ejes de simetría pueden combinarse en la misma figura atravesando vértices y también lados.

John Conway clasificó estas simetrías usando una letra y el orden de la simetría a continuación. Asignó la letra r al grupo de simetría de la figura regular; y en el caso de los subgrupos utilizó la letra d (de diagonal) para las figuras con ejes de simetría solo a través de sus vértices; p para figuras con ejes de simetría solo a través de ejes perpendiculares a sus lados; i para figuras con ejes de simetría tanto a través de vértices como a través de centros de lados; y g para aquellas figuras solo con simetría rotacional. Con a1 se etiquetan aquellas figuras con ausencia de simetría. Los tipos de simetrías más bajos permiten disponer de uno o más grados de libertad para definir distintas figuras irregulares. Solo el subgrupo g20 no tiene grados de libertad, pero puede verse como un grafo dirigido. (Véase un ejemplo en la Teoría de grupos de John Conway)

Los isodecágonos irregulares de mayor simetría son $d20$ , un isodecágono isogonal construido por diez reflexiones que pueden alternar aristas largas y cortas, y $p20$ , un isodecágono isotoxal, construido con longitudes de borde iguales, pero vértices alternando dos ángulos internos diferentes. Estas dos formas son duales entre sí y tienen la mitad del orden de simetría del isodecágono regular.

Disección

20-gono diseccionado en 180 rombos
regular	Isotoxal

Harold Scott MacDonald Coxeter estableció que cada zonágono (un $2 m$ -gono cuyos lados opuestos son paralelos y de igual longitud) se puede diseccionar en $m (m -1)/2$ paralelogramos.

En particular, esto es cierto para los polígonos regulares con muchos lados, en cuyo caso los paralelogramos son todos rombos. En el caso del isodecágono, $m =10$ , se puede dividir en 45: 5 cuadrados y 4 conjuntos de 10 rombos. Esta descomposición se basa en una proyección en forma de polígono de Petrie de un decaracto, con 45 de sus 11520 caras. La lista A006245 enumera el número de soluciones como 18.410.581.880, incluyendo rotaciones de hasta 20 veces y formas quirales en reflexión.

Disección en 45 rombos
decaracto

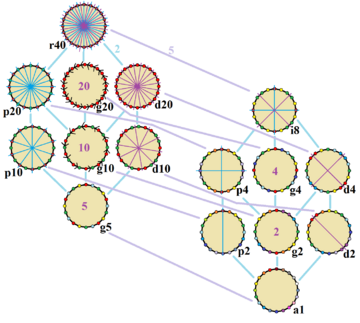
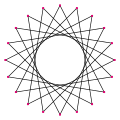
Polígonos relacionados

Un icosagrama es un estrella de 20 lados, representada por el símbolo ${20/n}$ . Existen tres formas regulares dadas por los símbolos de Schläfli: ${20/3}$ , ${20/7}$ y ${20/9}$ . También hay cinco figuras de estrellas regulares (compuestas) que usan la misma disposición de vértices: $2{10}$ , $4{5}$ , $5{4}$ , $2{10/3}$ , $4{5/2}$ y $10{2}$ .

n	1	2	3	4	5
Forma	Polígono convexo	Compuesto	Polígono estrellado	Compuesto
Imagen	{20/1} = {20}	{20/2} = 2{10}	{20/3}	{20/4} = 4{5}	{20/5} = 5{4}
Ángulo interior	162°	144°	126°	108°	90°
n	6	7	8	9	10
Forma	Compuesto	Polígono estrellado	Compuesto	Polígono estrellado	Compuesto
Imagen	{20/6} = 2{10/3}	{20/7}	{20/8} = 4{5/2}	{20/9}	{20/10} = 10{2}
Ángulo interior	72°	54°	36°	18°	0°

Los truncamientos más profundos del decágono regular y del decagrama pueden producir formas de icosagramas intermedios isogonales (figura isogonal) con vértices igualmente espaciados y dos longitudes de arista distintas.

Un icosagrama regular, ${20/9}$ , puede verse como un decágono cuasi truncado, $t{10/9}={20/9}$ . De manera similar, un decagrama, ${10/3}$ posee un cuasitruncamiento $t{10/7}={20/7}$ , y finalmente un decagrama simplemente truncado permite obtener $t{10/3}={20/3}$ .

Icosagramas como truncamientos de decágonos y decagramas regulares, {10}, {10/3}
Cuasirregular					Cuasirregular
t{10}={20}					t{10/9}={20/9}
t{10/3}={20/3}					t{10/7}={20/7}

Polígonos de Petrie

El isodecágono regular es el polígono de Petrie para una serie de politopos de dimensiones superiores, que se muestran en proyecciones oblicuas sobre el plano de Coxeter:

A₁₉	B₁₀		D₁₁	E₈	H₄	½2H₂	2H₂
símplex	10-ortoplex	decaracto	11-demicubo	(4₂₁)	hexacosicoron	Gran antiprisma	10-10 duopirámide	10-10 duoprisma

También es el polígono de Petrie para 120-cell icosaedral, 120-cell estrellado pequeño, 120-cell icosaedral grande y 120-cell gran grande.

Véase también

En inglés: Icosagon Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Isodecágono&oldid=3869421»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Isodecágono para Niños. Enciclopedia Kiddle.

Isodecágono para niños